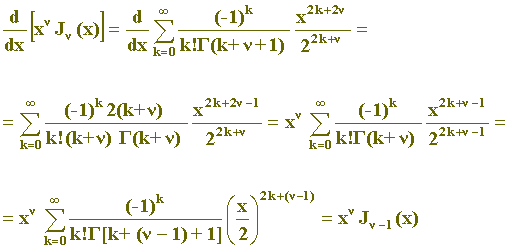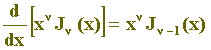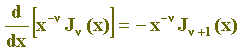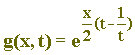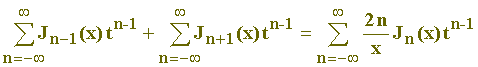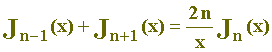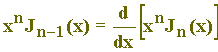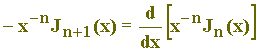A Equação de Bessel
Alberto Mesquita Filho
Integração II(5):101-6,1996
2ª. Parte
5 Fórmulas de recorrência das funções de Bessel
As fórmulas de recorrência das funções de Bessel são relações entre funções de Bessel de ordens diferentes. São extremamente úteis, possibilitando, por exemplo, que se expresse uma dada função J
em termos de funções de Bessel de ordem mais baixa [8]; prestam-se também à redução de certas integrais que ocorrem na normalização das funções de Bessel [9].
A título de clareza, e com a finalidade de destacá-las, iremos numerá-las em algarismos romanos, conservando a numeração sequencial em algarismos arábicos para as demais equações. Nas demonstrações referentes às equações (I) e (II) serão feitas algumas restrições com respeito a
. Apesar destas restrições, demonstra-se que (I) e (II) são válidas "
ÎÂ. Chegaremos a essa generalização por outro método — a partir da função geratriz — a ser visto no próximo item.
I) Se


:
Portanto:
- (I)
II) Se -

Z+:

Portanto:
- (II)
III) Desenvolvendo o primeiro membro de (I), temos:
x
J'
(x) +
x
-1J
(x) = x
J
-1(x).
Podemos dividir todos os termos por x
-1, tendo em vista que, de (1), x ¹ 0. Portanto:
- (III)
IV) De maneira análoga, desenvolvendo o primeiro membro de (II) e a seguir dividindo todos os termos da equação resultante por x-
-1:
x-
J'
(x) +
x-
-1J
(x) = - x-
J
+1(x)
- (IV)
V) Somando membro a membro (III) e (IV):
- (V)
VI) Subtraindo membro a membro (IV) de (III):
- (VI)
6 Função geratriz
Geratriz significa aquela que gera. Nesse contexto, mostraremos a seguir que
é função geratriz da função de Bessel de primeira espécie Jn(x) para n
Z.
Desenvolvendo g(x,t) obtemos:
Seja então n tal que n = r - k. Nestas condições, r = k + n e n varia de -
a +
. Então:
Portanto:
- (16)
Verificada a igualdade (16) podemos agora, a partir da mesma, demonstrar a validade das relações de recorrência (I) a (VI) para
= n
Z. E, com efeito, derivando (16) em relação a t e desenvolvendo a expressão resultante, temos:
Igualando os expoentes de t a n-1:
Portanto:
- (VIa)
A expressão (VIa) corresponde à (VI) para

Z.
Derivando (16) em relação a x:
Igualando os expoentes de t a n
Portanto:
- (Va)
A expressão (Va) corresponde à (V) para

Z.
As demais relações de recorrência derivam de (Va) e (VIa) da seguinte forma:
(Va) + (VIa) Þ (IIIa) ;
(VIa) - (Va) Þ (IVa) ;
(IIIa)
xn-1 Þ xnJn-1(x) = nxn-1Jn(x) + xnJ’n(x) Þ
- (Ia)
(IVa)
x-n-1 Þ -x-nJn+1(x) = -nx-n-1Jn(x) + x-nJ’n(x) Þ
- (IIa)
7 Ortogonalidade das Funções de Bessel
Sejam σ e μ dois autovalores da equação
- x2y" + xy’ + (l2x2 -
2)y = 0
- (17)
Nestas condições, e conforme visto no item 4,
- y1 = J
(σx)
- e
- y2 = J
(μx)
- (18)
são soluções da equação (17) para os correspondentes autovalores (l = σ e l = μ, respectivamente). Podemos então escrever:
- x2y1" + xy1' + (σ2x2 -
2)y1 = 0
- (19)
- x2y2" + xy2' + (μ2x2 -
2)y2 = 0
- (20)
Multiplicando (19) por y2 e (20) por y1 e subtraindo membro a membro as equações (20) da (19), assim modificadas, temos:
x2(y2y1"- y1y2") + x(y2y1'- y1y2') = (μ2 - σ2)x2y1y2
Dividindo por x e manipulando os termos, podemos escrever:
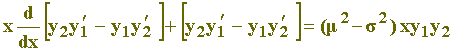
ou
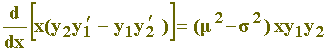
- (21)
Integrando (21) no intervalo [a,b]:
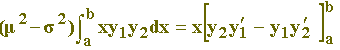
Dividindo por (μ2 - σ2) e utilizando as igualdades (18):

Para a=0 e b=R, temos:

- (22)
e para μ Þ σ a expressão fica:

Aplicando L’Hospital e a seguir multiplicando o numerador e o denominador do segundo membro da expressão por σ:
-
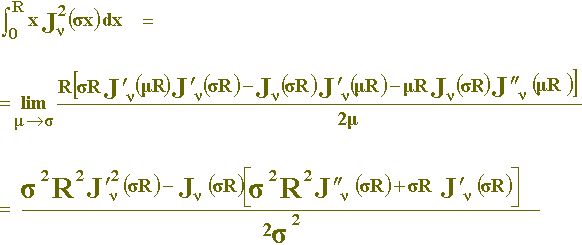
- (23)
Mas J(σR) é solução da equação de Bessel
σ2R2y"(R) + σRy’(R) + (σ2R2 - 2)y(R) = 0,
ou seja
- σ2R2J
"(σR) + σRJ
’(σR) = - (σ2R2 -
2)J
(σR).
- (24)
Substituindo (24) em (23):
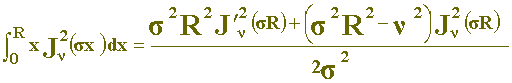
ou
-
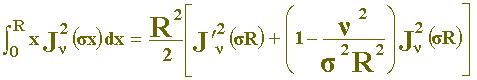
- (25)
Se σ,
μ e R forem tais que as raízes n-ésima e m-ésima da função de Bessel de ordem igualem, respectivamente a
α
n =
σR e
α
m=
μR, as expressões (22) e (25) podem ser agrupadas numa única expressão:
-
 (*)
(*) - (26)
conhecida como relação de ortogonalidade das funções de Bessel. De (26) observa-se
que as funções ![]()
 e
e ![]()
 são ortogonais no intervalo [0,R]; ou então, as
funções
são ortogonais no intervalo [0,R]; ou então, as
funções  e
e  são
ortogonais em relação à função peso x.
são
ortogonais em relação à função peso x.
* * * * *
8. CHURCHILL, R.V., BROWN, J.W, (1987), Fourier Series and Boundary Value Problems, McGraw-Hill Book Company, New York.
9. PINSKY (1991), op. cit.
(*) δn,m = 0 se n ¹ m, e δn,m = 1 se n = m. Observar que se n ¹ m, a equação válida é a (22), e se n = m (ou μ Þ σ) recaímos na equação (25). Como estamos trabalhando com raízes, J(σR) = J
(μR) = 0 em ambos os casos, o que nos leva facilmente à generalização expressa em (26).