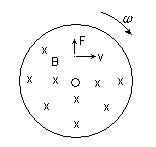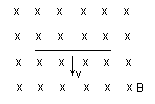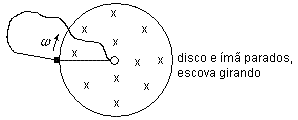Reinterpretando o paradoxo de Faraday
Belmiro Wolski
© 2010
Divulgação autorizada para o ECC
Introdução: O funcionamento do gerador homopolar, inventado pelo próprio Michael Faraday em 1831, tem sido alvo de inúmeras discussões que persistem até hoje no meio científico. O estranho comportamento aparentemente desafia o bom senso e a relatividade do movimento, e por esta razão é conhecido como “o paradoxo de Faraday”. Alguns trabalhos afirmam que é o único caso em que a tensão induzida não pode ser explicada pela Lei de Faraday. O objetivo deste trabalho é defender a universalidade da Lei de Faraday, mostrando que ela também se aplica ao gerador homopolar.
Abstract: The homopolar generator is a simple machine, created by Faraday in 1831. Is an application of electomagnetics induction’s law discovered by himself, also well-known as Faraday’s Law. Consists in a aluminum disc that spins into a magnetic field, and the energy is capted by brushes in the center and the rim of the disc. The curiosity about this machine is the apparently violation of the relativity movement´s, because no energy is obtained when the magnetic field is in movement and the disc is stationary. In literature, this fact puts in doubt the Faraday’s Law application. In present work, we pretend demonstrate that Faraday’s Law is applicable in whole cases.
Palavras-chave: Fluxo magnético, Lei de Faraday, disco, força eletromotriz, polaridade.
Key-words: Magnetic flux, Faraday’s Law, disc, induced emf, polarity.
Referências:
- Revista Brasileira de Ensino de Física, vol. 29, n03, São Paulo 2007.
- O Gerador de Faraday - Manuel Vaz Guedes
- Homopolar generator - Wikipedia
- Homopolar Generator - Brown University
1 – O gerador homopolar
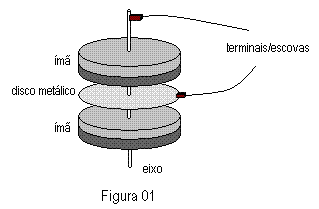
O gerador homopolar consiste de um disco metálico, livre para girar em torno de seu eixo de simetria, e de um ímã permanente também em formato de disco, cujos pólos envolvem o disco metálico. Os pólos do ímã são também acoplados a um eixo de forma que tanto o disco quanto os pólos podem executar movimentos de rotação. A tensão gerada é coletada por escovas que deslizam uma na borda do disco e outra no eixo acoplado ao disco. O esquema do gerador homopolar pode ser visto na figura 01 abaixo.
2 – Funcionamento
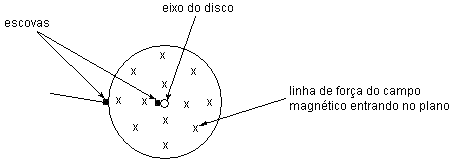
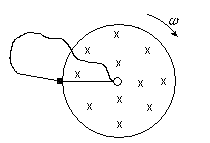
O funcionamento do gerador homopolar se dá quando o disco é posto a girar dentro do campo magnético, inicialmente mantido estacionário. Vamos mostrar o disco em vista superior com o campo magnético do ímã sendo representado pelas suas linhas de força penetrando no plano do papel, como mostrado na figura 02 abaixo.
Figura 02Com o movimento do disco, todas as cargas elétricas contidas no mesmo, ficam sujeitas à força de Lorentz, segundo a equação:
Admitindo-se que o disco esteja girando com velocidade angular w, cada ponto do disco estará sujeito a uma velocidade tangencial dada por
, onde r é a distância radial do ponto. Desta forma, as cargas livres presentes no disco serão deslocadas pela ação da força:
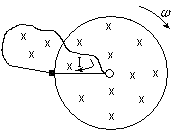
Na figura 03 abaixo, é ilustrada a força sobre uma carga positiva localizada em um determinado ponto do disco.
Figura 03O sentido da força foi determinado pelo produto vetorial da equação da força de Lorentz, utilizando-se a conhecida regra do tapa. As forças atuando sobre as cargas livres, promoverão uma redistribuição de cargas no disco, como mostrado na figura 04 abaixo.
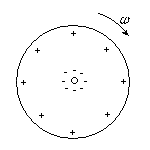
Figura 04A força eletromotriz gerada entre qualquer ponto na borda do disco e o centro será a mesma, o que nos permite calculá-la, considerando apenas um filete radial do disco. Então, sobre este filete, temos:
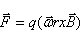
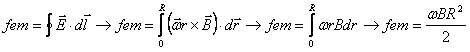
Os sinais de vetores dentro da integral foram eliminados pelos produtos vetorial e escalar e a integral no percurso fechado se resume à integral sobre o raio do disco, haja vista não haver cargas no restante do percurso.
3 – O paradoxo de Faraday
Vimos que ao girarmos o disco no interior do campo magnético, gera-se entre a borda e o centro do disco uma força eletromotriz dada por:
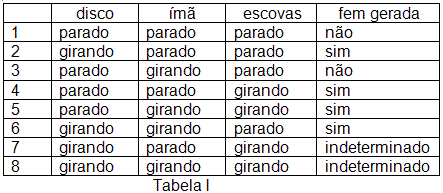
. Considerando-se a relatividade do movimento, é de se esperar que, ao girarmos o imã, mantendo o disco parado, obtenhamos o mesmo valor para a força eletromotriz. Entretanto, não é o que a prática nos mostra. Nestas condições, a força eletromotriz gerada é nula. É nisto que consiste o paradoxo de Faraday. Depois de constatado este fato, o próprio Faraday se encarregou de realizar outras experiências, alterando os elementos em movimento, entre eles o sistema de escovas. Todas as possibilidades estão ilustradas na tabela I abaixo:
4 – Variação de fluxo
Como dito anteriormente, coloca-se em dúvida a aplicabilidade da Lei de Faraday em relação ao gerador homopolar, devido ao fato de não ficar claro como o fluxo varia.
Tomemos o caso de um condutor de comprimento determinado, se deslocando no interior de um campo magnético constante, conforme figura 05 abaixo.
Figura 05Podemos determinar a força eletromotriz gerada no condutor mediante a aplicação da equação da força de Lorentz:
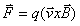
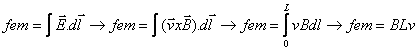
Pela regra do tapa para o produto vetorial, podemos concluir que o lado direito do condutor possui polaridade positiva.
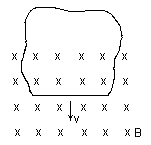
Podemos também determinar a polaridade da força eletromotriz, considerando-se a variação de fluxo que o condutor sofre ao se deslocar de uma posição a outra dentro do campo magnético. Para isto, podemos associar às pontas do condutor, um percurso imaginário que feche o circuito. Esse percurso deve ficar mentalmente imóvel em relação ao condutor e, necessariamente, deve estar parcialmente fora do campo magnético, para que a variação de fluxo sobre ele possa ser observada. Um possível percurso fechado está mostrado na figura 06 a seguir:
Figura 06Neste caso, com o avanço do condutor e do percurso imaginário a ele vinculado para baixo, o fluxo magnético no interior do circuito fechado está variando de forma crescente. Pela lei de Faraday, se o fluxo está variando, então há uma força eletromotriz induzida atuando no condutor. E, pela lei de Lenz, a polaridade da força eletromotriz induzida deve ser tal que tenda a estabelecer uma corrente no percurso fechado para criar um campo magnético que se oponha ao tipo de variação de fluxo que estiver ocorrendo. Como o fluxo está aumentando e aponta para dentro do plano do papel, então essa corrente deveria circular no sentido anti-horário através do percurso fechado, de forma a criar um fluxo apontando para fora do plano do papel. Assim, observamos que essa hipotética corrente deveria sair pelo lado direito do condutor, o qual então, obviamente é positivo. Isto corrobora a polaridade obtida anteriormente através da regra do tapa.
O mesmo resultado seria obtido se tivéssemos escolhido um percurso imaginário voltado para baixo do condutor. Neste caso, o fluxo no interior do percurso estaria diminuindo o que forçaria a criação de uma corrente no sentido horário através do percurso, o que coincide com o mesmo sentido de corrente através do condutor.
Para determinar o valor da força eletromotriz não se pode fazê-lo determinando a taxa de variação de fluxo sobre o percurso todo, incluindo o imaginário. Com isto estaríamos determinando a força eletromotriz sobre o percurso todo e não somente sobre o condutor, como é de nosso interesse. Desta forma temos que imaginar a variação de fluxo sofrida pelo condutor ao sair de uma posição inicial e chegar a uma posição final varrendo uma distância incremental dx num tempo dt. A variação de fluxo será: df = BdS, onde dS = Ldx, sendo L o comprimento do condutor e dx o deslocamento incremental sofrido pelo condutor no tempo dt. Desta forma, a força eletromotriz será:
Observação: O sinal negativo no resultado foi omitido neste caso, pois, ele é inútil para indicar a polaridade, visto que não há um referencial adotado.
5 – Variação de fluxo no gerador homopolar
Comportamento do gerador homopolar nas diversas situações.
Na tabela I, para a situação 1, obviamente a força eletromotriz gerada é nula, pois disco, imã e escova estão parados. Vamos agora analisar a situação 2.
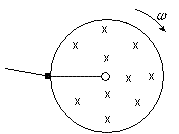
Como vimos no item 2, a força eletromotriz é simétrica radialmente. Na figura 07 a seguir, tomamos uma linha radial que intercepta um ponto da escova da borda do disco. A escova que toca o eixo foi omitida, para facilitar a visualização, o que não prejudica a análise, mesmo porque ela não precisa estar necessariamente no mesmo plano da escova da borda.
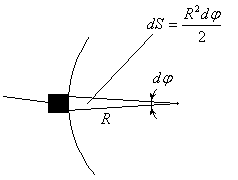
Figura 07Todas as cargas contidas nesta linha viajam, vinculadas ao disco, com velocidade angular w. Durante o tempo que esta linha fica em contato com a escova, o que depende da largura desta última e da velocidade angular w, teremos o fluxo magnético variando sobre a linha. Consideremos um instante de tempo qualquer em que a linha está tocando a escova. Um instante de tempo dt depois, a linha varreu uma área correspondente a um setor circular como mostrado na figura 08 a seguir:
Figura 08A correspondente variação de fluxo sofrida pela linha de cargas será df = BdS. Assim, a força eletromotriz será:
onde novamente desconsideramos o sinal negativo no resultado.
Observa-se que a força eletromotriz obtida é a mesma que a encontrada pela equação da força de Lorentz. Para determinar a polaridade da força eletromotriz, utilizamos o artifício do percurso fechado imaginário. Adotando então um percurso arbitrário como ilustrado na figura 09 a seguir, observamos que o fluxo magnético está diminuindo em seu interior.
Figura 09Por conta disto, a hipotética corrente que deveria circular, teria o sentido horário através do percurso, de forma a criar um fluxo no mesmo sentido que o do ímã, conforme ilustração a seguir.
Figura 10Concluímos assim que, a polaridade do ponto correspondente à escova externa, ou seja, a borda do disco é positiva.
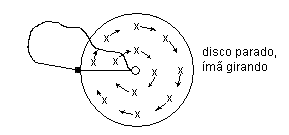
Para justificar o comportamento do gerador homopolar na situação 3 da tabela I, imaginemos a figura 11 abaixo.
Figura 11Quando o disco está parado e o ímã girando, não se observa variação de fluxo sobre o percurso fechado. A linha de cargas, considerada como parte integrante do percurso fechado, não se move. Desta forma, o percurso se mantém sempre o mesmo. Como o campo magnético é uniforme, cada linha de força que deixa o percurso fechado é imediatamente reposta por uma linha que entra pelo lado oposto. Sendo assim, a variação de fluxo resultante no percurso fechado é nula, tornando nula também a força eletromotriz.
Na situação 4, disco e ímã estão parados e a escova está em movimento, havendo força eletromotriz gerada.
Figura 12Considerando o mesmo percurso fechado imaginário, percebemos que, com o movimento da escova, a cada instante uma nova linha de cargas radial toca a escova. Isto é equivalente a uma única linha de cargas que se desloca, promovendo uma variação de fluxo no interior do percurso fechado. Como tal, uma força eletromotriz é gerada. Observa-se que o gerador homopolar nesta situação se comporta como o analisado na situação 2.
Para analisar a situação 5, observemos que na situação 3, não há força eletromotriz gerada quando o ímã está em movimento e o disco e escova estão parados, justamente porque não há variação de fluxo. Comparando com a situação 1, observamos que é indiferente se o ímã está ou não em movimento quando disco e escovas estão parados. Logo, a situação 5 é equivalente a situação 4.
Pelo mesmo raciocínio, a situação 6 é equivalente à situação 2, pois novamente é indiferente se o ímã está ou não em movimento.
Nas situações 7 e 8, vai depender apenas da maneira como o disco e a escova estão girando, haja vista que o movimento do ímã não irá afetar a tensão gerada. Desta forma, se disco e escova girarem de forma que haja movimento relativo entre eles, haverá força eletromotriz gerada. Caso contrário, a força eletromotriz será nula.
Conclusão
Do exposto no trabalho acima, conclui-se que a Lei de Faraday também se aplica ao caso do gerador homopolar e que a polaridade da tensão gerada pode ser determinada pelo método da variação de fluxo em um circuito fechado imaginário.
* * * * *
Belmiro Wolski é professor do Departamento Acadêmico de Eletrotécnica da Universidade Tecnológica Federal do Paraná, UTFPR.
Leia, do mesmo autor:
Análise Alternativa de Interações Magnéticas