Alberto Mesquita Filho
Integração II(4):26-30,1996
Quando
dizemos que a filosofia não nos
interessa, o que provavelmente fazemos é substituir uma filosofia
explícita por outra implícita, isto é, imatura e incontrolada. [...]
Esta filosofia caseira [...] supõe que um símbolo, tal como uma equação,
possui significado físico somente à medida que diga respeito a alguma
possível operação humana. Isto equivale a se considerar a totalidade da
física como se referindo a operações, principalmente medições e
cálculos, e não à natureza, o que implica num retorno ao
antropocentrismo prevalecente antes do nascimento da ciência.
Mario Bunge [1]
Sumário: Sabe-se, desde as primeiras décadas do século XX, que o elétron, ao contrário de uma carga elétrica clássica, assume, com grande freqüência, um comportamento anômalo quando de sua exploração experimental, chegando mesmo a dar-nos a impressão de tratar-se de uma partícula paranormal. Por vezes parece estar dotado de propriedades que o situam numa outra dimensão ou num universo paralelo ao nosso. Não obstante, aceita-se, tal e qual um dogma travestido de paradigma "kuhniano" [2], sua natureza "maxwelliana". Em outras palavras, excetuando-se tais fenômenos mirabolantes, somente decifrados através da matemática quântica, admite-se, sem qualquer apelo a uma comprovação experimental rigorosamente lógica, que o elétron apresenta um comportamento idêntico ao de uma carga elétrica "coulombiana". Recentemente publiquei uma teoria a respeito do elétron [3] que se apoia na negação do paradigma citado. Neste artigo pretendo resumir, ou até mesmo evoluir, alguns tópicos essenciais da teoria, remetendo, a sua fonte, o leitor interessado nos detalhes axiomáticos ou heurísticos.
1. Introdução
São inúmeras as experiências realizadas no século XX a sugerir, por um lado, a natureza discreta dos agentes reponsáveis pelos fenômenos eletromagnéticos e, por outro, a natureza não coulombiana destas partículas. Contrapõe-se a estas evidências experimentais, a beleza das equações de Maxwell, frutos de uma teoria que sintetizou e coroou os esforços dos cientistas do século passado ao caracterizarem o que julgavam tratar-se de um fluido: o fluido elétrico. Hoje não há mais porque se pensar em fluidos elétricos; e ao supor que o elétron é a fração elementar da carga elétrica, posto que uma carga elétrica é composta por eletrons, incorre o físico no mesmo erro que um filósofo ingênuo incorreria se admitisse que o átomo tem o formato de um avião, posto que um avião é formado por átomos.
Mas se os eletrons não são cargas coulombianas, como os mesmos conseguem se agrupar a ponto de originar uma carga elétrica que gera um campo elétrico E coulombiano? De que forma eletrons e protons se dispõem, num condutor submetido a uma diferença de potencial, de forma a gerar um campo B dado pela lei de Ampère-Laplace? Qual é o campo de um elétron, e como e porque tais campos se associam assumindo disposições maxwellianas? Dentre os campos maxwellianos: Quais são os lorentzianos? Ou seja, aqueles nos quais um elétron obedece à equação de Lorentz, como se possuísse uma carga elétrica?
A física moderna não responde a estas perguntas; e nem poderia, posto que tanto a teoria da relatividade quanto a física quântica se apóiam no absurdo apontado no parágrafo primeiro desta introdução. Resta-nos então seguir a lógica clássica, e desta forma, nos itens que seguem, procurarei desenvolver o arcabouço matemático necessário para que se possa chegar a um eletromagnetismo fundamentado no conceito de partículas, e não no de fluidos elétricos.
2. Modelo matemático do campo de um elétron
Vamos admitir inicialmente que
o elétron possa ser representado matematicamente por sua posição
P = P(x,y,z) associada a um versor
![]() que retrata aspectos qualitativos de sua estrutura interna, e por
um escalar K responsável pela quantificação dos fenômenos
eletromagnéticos relacionados ao mesmo. Seja ainda
φ = φ(x,y,z) um campo definido, em um ponto
Q = Q(x,y,z) exterior ao elétron, através da expressão:
que retrata aspectos qualitativos de sua estrutura interna, e por
um escalar K responsável pela quantificação dos fenômenos
eletromagnéticos relacionados ao mesmo. Seja ainda
φ = φ(x,y,z) um campo definido, em um ponto
Q = Q(x,y,z) exterior ao elétron, através da expressão:
|
(1) |
sendo r a distância de P a Q. Definirei ainda os campos xi e bi, de um elétron i, relacionados ao que chamarei efeitos elétrico (x) e magnético (b), por:
xi
= Ñφi
Ä
|
e |
bi
= Ñφi ×
|
(2) |
sendo que Ä opera entre dois vetores originando um terceiro quantificado pelo produto escalar ou interno entre os mesmos, e cuja direção é a do segundo vetor, ou seja, aquele que, na expressão considerada, aparece à direita de Ä. Direi então que xi é o produto vetorial interno entre os vetores Ñφi e wi e, afim de evitar confusões, direi que bi é o produto vetorial externo entre os mesmos vetores, conquanto seja, nada mais, nada menos, que o produto vetorial clássico.
É interessante observar que a função φ, dada por (1), goza das seguintes propriedades:
|
ÑφÄ Ñφ´ |
(3) |
ou seja, é possível definir um vetor
Ai =
φi![]() tal que
tal que
xi = ÑÄAi |
e |
bi = Ñ´Ai |
(4) |
Desenvolvendo as expressões (2) relativas aos produtos vetoriais xi e bi obtém-se:
|
(5) |
Existem, em teoria, dois agrupamentos infinitesimais de elétrons extremamente interessantes:
- o elemento de superfície da povoado por dn = σda elétrons cujos
são paralelos entre si e perpendiculares à superfície;
- o elemento de volume dV povoado por dn = ρ dV elétrons também paralelos entre si.
Decorre de (5), e admitindo-se a validade do princípio de superposição, que os campos de efeitos elétricos dx e magnéticos db das populações infinitesimais assim definidas, são:
a) Elemento de Superfície
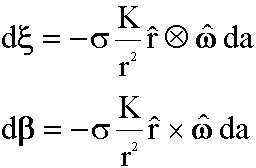 |
(6a) |
b) Elemento de Volume
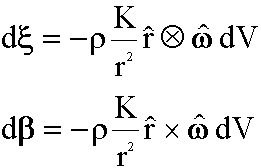 |
(6b) |
Os
elementos da e dV,
da maneira como foram definidos, representam uma ponte entre o
microcosmo, ou o mundo das partículas elementares, e o universo no qual
as equações de Maxwell adquirem importância prática. Desta forma, se
pensarmos numa superfície esférica fechada, composta por elementos
da, obtemos, pela integração das expressões
(6a) um campo b = 0 e um
campo x matematicamente
idêntico ao campo E de uma carga coulombiana, quando no
exterior da esfera [4]. Por outro lado, se
efetuarmos a integração de dV dado por (6b) para um fio retilíneo e de
espessura infinitesimal, e tal que os ![]() se orientem segundo seu eixo, chegaremos a um campo
x = 0 e a um campo
b matematicamente idêntico
ao campo B da lei de Ampère-Laplace. Apesar deste parentesco
matemático deve-se notar que os campos
x e
b de quaisquer
agrupamentos de eletrons são conceitualmente, e portanto
físico-matematicamente, distintos dos campos E e B da
teoria de Maxwell.
se orientem segundo seu eixo, chegaremos a um campo
x = 0 e a um campo
b matematicamente idêntico
ao campo B da lei de Ampère-Laplace. Apesar deste parentesco
matemático deve-se notar que os campos
x e
b de quaisquer
agrupamentos de eletrons são conceitualmente, e portanto
físico-matematicamente, distintos dos campos E e B da
teoria de Maxwell.
Conforme visto no parágrafo
anterior, é possível se pensar numa carga elétrica coulombiana,
em particular aquela localizada num condutor esférico, como sendo
redutível a elementos infinitesimais da
cujo campo dx é dado por
(6a). Isto, por si só, sugere a existência real do campo
x, bem como nos estimula
a evoluir um pouco mais no sentido da matemática à física. Com efeito,
e até o momento, assumimos a validade de uma série de equações sem nos
preocuparmos com os referenciais nos quais as mesmas são descritas.
Pode-se no entanto perceber que tais equações se mostram consistentes
apenas no referencial do laboratório de Coulomb, ou seja, naquele em
que vivemos. Mas não é esse o mesmo referencial em relação ao qual
Newton deduziu suas leis da mecânica? Ou, se quisermos ser mais
rigorosos, as leis de Newton não são válidas num referencial muito
próximo daquele em que vivemos, e ao qual se convencionou chamar
referencial inercial? Mas o que é um referencial inercial? Direi que
um referencial inercial é aquele no qual um elétron, que
mantenha constantes suas características P e
![]() ,
gera campos x e
b [5]
dados pelas equações (5).
,
gera campos x e
b [5]
dados pelas equações (5).
A título de brevidade,
chamarei por referencial próprio àquele no qual o elétron em
estudo mantém P e ![]() constantes. Este é o referencial apropriado para a análise matemática
do campo eletromagnético do elétron posto que o mesmo é função de K,
constantes. Este é o referencial apropriado para a análise matemática
do campo eletromagnético do elétron posto que o mesmo é função de K,
![]() e
e ![]() . Em particular, se
o referencial próprio for um referencial inercial, o campo
eletromagnético do elétron é função apenas destas três variáveis,
conforme se pode avaliar pelo estudo das equações (5). Pode-se também
dizer, com restrições, que o referencial próprio é aquele no qual o
elétron está em repouso; as restrições justificam-se, tendo
em vista que não foram explicitadas hipóteses sobre a estrutura
interna do elétron. Consequentemente, este repouso não leva em
consideração uma possível estrutura dinâmica para o
elétron.
. Em particular, se
o referencial próprio for um referencial inercial, o campo
eletromagnético do elétron é função apenas destas três variáveis,
conforme se pode avaliar pelo estudo das equações (5). Pode-se também
dizer, com restrições, que o referencial próprio é aquele no qual o
elétron está em repouso; as restrições justificam-se, tendo
em vista que não foram explicitadas hipóteses sobre a estrutura
interna do elétron. Consequentemente, este repouso não leva em
consideração uma possível estrutura dinâmica para o
elétron.
Os referenciais próprios não inerciais [6] subdividem-se em duas categorias:
- aqueles nos quais o campo eletromagnético é função periódico-estacionária do tempo; constituem exemplos importantes os campos produzidos por elétrons ou prótons constituintes de átomos e moléculas em suas configurações estáveis.
- aqueles nos quais o campo eletromagnético é uma função não periódico-estacionária do tempo; dizemos, nestas condições, que o elétron emite radiação eletromagnética.
É de se notar que a teoria de Maxwell não comporta este tipo de classificação para os referenciais.
No restante deste artigo, salvo disposição em contrário, admitirei que os referenciais próprios considerados são inerciais. Convém, então, distinguir duas condições particulares:
3.1 Observador situado no referencial próprio (inercial)
Neste caso os campos x e b estão bem definidos. Destaca-se, em oposição ao eletromagnetismo clássico, a existência de um campo de efeitos magnéticos originado por agentes causais em repouso. Observa-se ainda que o parentesco matemático entre o campo dB de um elemento de corrente (lei de Biot-Savart) e o campo db do elemento de volume dV dado por (6b) não é fortuito. Ao que tudo indica, e ao contrário do que afirma a teoria dos elétrons livres de Drude e Lorentz [7], o campo dB de um elemento de corrente, a exemplo de db, depende da densidade de carga eletrolítica do circuito, ou seja, do número de partículas efetivamente transportadas por unidade de volume, e não da velocidade dos agentes causais. Os possíveis efeitos relativísticos, no sentido clássico do termo, são desprezíveis no que tange à gênese destes campos.
O escalar K, da expressão (1), parece conter segredos relacionados aos referenciais inerciais, que somente a física experimental pode decifrar. Seria extremamente interessante verificar se o seu valor absoluto, uma vez definido, permanece ou não idêntico, qualquer que seja o referencial inercial considerado. A variabilidade de K seria um indício fortemente sugestivo a corroborar a intuição de Newton quanto à existência de um referencial absoluto.
3.2 Observador situado em referenciais impróprios:
De acordo com a teoria de
Maxwell, e seguindo a nomenclatura adotada neste artigo, o campo
magnético B é uma exclusividade dos referenciais impróprios.
Como vimos, isto não ocorre com
b e, portanto, não há
porque nos preocuparmos com justificativas sobre sua suposta origem
relativista. O importante é notar que
x e
b estão interligados
através de φ e ![]() ¾ equações
(2),¾ e, consequentemente,
caso ocorra a modificação de um destes campos, quando da mudança de
referencial, é de se esperar que o efeito tenha repercussão sobre o
outro.
¾ equações
(2),¾ e, consequentemente,
caso ocorra a modificação de um destes campos, quando da mudança de
referencial, é de se esperar que o efeito tenha repercussão sobre o
outro.
Os campos
x e
b, quando observados de
referenciais impróprios, manifestam um efeito que se relaciona a um
fenômeno descrito por Liénard (1898) e Wiechert (1900) para os
potenciais da teoria de Maxwell. Este efeito deve ser analisado com
extrema cautela posto que x
e b são funções de duas
variáveis: φ e ![]() . Ambas contribuições são interessantes, porém aquela
devida a
. Ambas contribuições são interessantes, porém aquela
devida a ![]() assume extrema importância epistemológica, visto ser a que, ao não
ser levada em conta, gera conseqüências funestas para a física
clássica. A desconsideração desta parcela, a meu ver, colocou em
evidência a pedra fundamental sobre a qual se apoiou a teoria da
relatividade de Einstein. Vamos então, e por etapas, evoluir o modelo
matemático apresentado, em busca da justificação do efeito
Liénard-Wiechert.
assume extrema importância epistemológica, visto ser a que, ao não
ser levada em conta, gera conseqüências funestas para a física
clássica. A desconsideração desta parcela, a meu ver, colocou em
evidência a pedra fundamental sobre a qual se apoiou a teoria da
relatividade de Einstein. Vamos então, e por etapas, evoluir o modelo
matemático apresentado, em busca da justificação do efeito
Liénard-Wiechert.
Em virtude de o campo (x, b), do elétron, poder ser expresso em termos de gradiente de uma função de posição φ, podemos conjecturar sobre a existência real de alguma coisa emitida pelo elétron, a que chamarei informação eletromagnética (i.e.m), e que se propaga para o espaço circunvizinho. O caráter de φ, dado por (1), sugere ainda mais: que as i.e.m., uma vez emitidas, se conservam, a menos que surja um sorvedouro em seu caminho. Em outras palavras, direi que o elétron é uma fonte emissora de i.e.m. e tal que o fluxo de i.e.m. que atravessa uma superfície qualquer se identifica com o fluxo de um campo vetorial h dado por
h = - Ñφ |
(7) |
Está implícito, nestas considerações, que h é do tipo
h = ρc , |
(8) |
sendo ρ um invariante que representa a densidade local de i.e.m., e c é a velocidade com que as mesmas se propagam no referencial próprio. Consequentemente, h se transforma segundo a expressão
h' = ρc' , |
(9) |
com c' = c + v, em que v é a velocidade do elétron emissor, quando observado do referencial impróprio considerado.
Vejamos agora como
![]() se transforma. Seja então um observador,
situado em um ponto Q de um referencial inercial, e um elétron
movendo-se, em relação a este referencial, com uma velocidade v
constante. Direi, então, que o versor
se transforma. Seja então um observador,
situado em um ponto Q de um referencial inercial, e um elétron
movendo-se, em relação a este referencial, com uma velocidade v
constante. Direi, então, que o versor ![]() se manifesta ao observador em Q sob a forma de um
outro versor
se manifesta ao observador em Q sob a forma de um
outro versor ![]() ’, ou seja,
’, ou seja, ![]() sofre uma aberração, conservando o seu módulo
unitário. Para o cálculo desta aberração, observados os pontos chaves
definidos na figura 1, deve-se proceder da seguinte forma:
sofre uma aberração, conservando o seu módulo
unitário. Para o cálculo desta aberração, observados os pontos chaves
definidos na figura 1, deve-se proceder da seguinte forma:
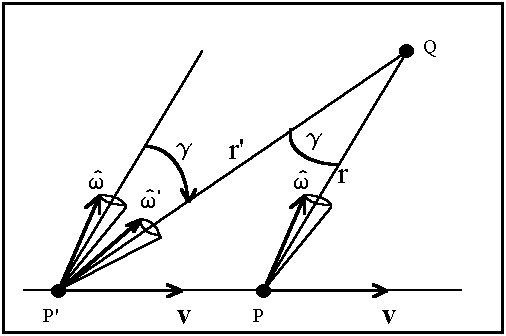 |
||
| Figura 1:Aberração de |
- determinar o ponto P', admitindo-se que "o campo se propaga" radialmente a uma velocidade c, quando analisada do referencial próprio;
- unir os pontos P, P' e Q;
- traçar por P um tronco de cone com vértice em P e que contenha
em sua superfície, e com eixo na direção PQ;
- transladar o cone juntamente com
para P';
- rotacionar o cone em torno de P' e segundo um eixo perpendicular ao plano da figura ¾ plano PP'Q ¾ até que o eixo do cone se situe na direção P'Q.
- o versor obtido por esta rotação de
é o versor
’.
4 O Campo (x, b) do Elétron em Movimento:
Conhecidas as transformações
conformes para h e ![]() ,
podemos desprezar os apóstrofos e assumir que os campos
x e
b de um elétron se
expressam matematicamente por
,
podemos desprezar os apóstrofos e assumir que os campos
x e
b de um elétron se
expressam matematicamente por
x
= -hÄ |
(10) |
seja nos referenciais próprios, seja nos referenciais impróprios. Decorre então de (10) que, qualquer que seja o referencial inercial considerado, a soma x² + b² é uma função relativística clássica de posição:
h² = x² + b² |
(11) |
De posse das transformações conformes, vamos agora analisar em que consistiria, para um elétron, o efeito observado por Liénard e Wiechert para cargas elétricas. O campo (x,b), para o elétron da figura 1, de acordo com (8), (9) e (10), pode ser expresso por:
| a) Referencial Próprio: | b) Referencial Impróprio: | |
| x = -
ρcÄ b = - ρc´ |
x'
= -
ρ(c +
v)Ä b' = - ρ(c + v)´ |
(12) |
Com o auxílio destas
expressões e da figura 2, verifica-se que, se não houvesse a aberração
de ![]() , o campo
(x',
b') seria, no ponto Q,
idêntico ao campo próprio que aí seria observado caso o elétron
ocupasse o ponto A; ou então, como se o elétron estivesse em P'
emitindo i.e.m. a uma taxa aparentemente mais elevada que a
real (ou aquela observada no referencial próprio). O efeito seria
análogo ao efeito Doppler da física ondulatória.
, o campo
(x',
b') seria, no ponto Q,
idêntico ao campo próprio que aí seria observado caso o elétron
ocupasse o ponto A; ou então, como se o elétron estivesse em P'
emitindo i.e.m. a uma taxa aparentemente mais elevada que a
real (ou aquela observada no referencial próprio). O efeito seria
análogo ao efeito Doppler da física ondulatória.
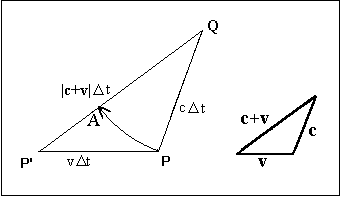 |
||
| Figura 2: Observam-se aqui os mesmos pontos da figura 1, enfatizando-se suas distâncias em função de c, v e Δt = t - t'. |
A idéia de um elétron em A não deve ser levada muito a sério. Com efeito, se recuarmos alguns parágrafos e analisarmos a maneira como o triângulo PP'Q foi construído, constataremos que, para qualquer outro ponto da vizinhança de Q, o ponto A da figura 2 não tem o mesmo significado, e, consequentemente, conquanto a analogia Doppler seja válida, a imagem em A tem apenas caráter especulativo, carecendo de significado físico-matemático.
O fenômeno complica-se um
pouco mais graças à aberração de ![]() .
Existem dois casos interessantes e particularíssimos:
.
Existem dois casos interessantes e particularíssimos:
- Aquele em que
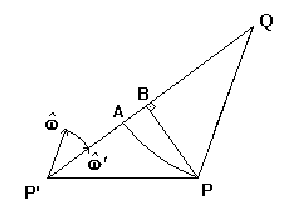
, no referencial próprio, ocupa a direção PQ: Neste caso, no que diz respeito a x, o ponto de identidade, acima descrito como A, desloca-se para B, ponto este mostrado na figura 3; além disso, o elétron imagem gira de um ângulo g, ou seja,
' ocupa a direção P'Q. Esta imagem também não resiste à crítica apontada anteriormente. Não obstante, se quisermos raciocinar em termos de efeito Doppler, devemos efetuar uma correção relativística devida à aberração de
. No que diz respeito a b, estamos frente a um limite impróprio: A sofre um deslocamento infinito, e a correção relativística é tal que a analogia Doppler se singulariza. Com efeito, b' = 0 (não apenas em Q, mas também em qualquer ponto de seu domínio que intercepte a reta que contém P e Q), tendo em vista que h' e
' são perpendiculares.
 |
||
Figura 3: Para a sua compreensão, vide o texto. |
- Aquele em que
', no referencial próprio, é perpendicular a PQ: Neste caso x e b trocam os seus papéis em relação ao comentado no caso anterior..
* * * * *
- BUNGE, M. (1982), Filosofia de la Fisica, Editorial Ariel, Barcelona, p.11. Voltar
- KUHN, T. S., A Função do Dogma na Investigação Científica, em A Crítica da Ciência, Jorge Dias (org.), Texto n.° 2, Zahar Editores, Rio, 1974, pp.53-80. Voltar
- MESQUITA F°., A. (1993), A Equação do Elétron e o Eletromagnetismo, Editora Ateniense, São Paulo. Voltar
- MESQUITA F°., A. (1993), op.cit. , pp. 99-102. Voltar
- idéia de definir referenciais inerciais a partir das equações de campo, é antiga. Não obstante, esta prática, conquanto essencial, não é muito enfatizada em livros de texto, posto que as teorias clássicas de campo têm-se mostrado, a esse respeito, incompatíveis entre si (o leitor poderá encontrar algo a respeito em BUNGE, M., Controversias en fisica, Editorial Tecnos S.A., Madri, pp. 88-92, ou então nos vários trabalhos que procuram justificar o nascimento da física relativista). Voltar
- Dizer que um elétron está em repouso em relação a um referencial não inercial é o mesmo que dizer que ele está sob a ação de forças newtonianas quando observado de um referencial inercial newtoniano. Voltar
- Este assunto é discutido em detalhes no livro citado na referência 3, pp. 27-31. Voltar
