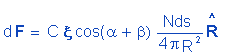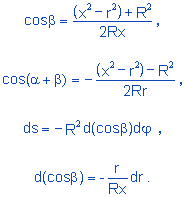4.1 Considerações sobre o método:

       Uma região do espaço é sede de um campo quando aí é possível caracterizar uma propriedade física dada por uma função da posição e do tempo [32]. Nesta definição está implícito um processo de medição que, para campos de interação, subentende um efeito sobre um objeto de prova. É importante notar que, para um mesmo campo, a propriedade observada pode ser diferente se os objetos de prova considerados forem diferentes. Feita esta ressalva e voltando à definição acima podemos concluir que o campo é caracterizado por seus efeitos e não por sua causa.

       O que dizer sobre o método? Ao se referir às dificuldades inerentes à elaboração de teorias eletromagnéticas de campo, Einstein comentou: A ausência de um método sistemático impediu-nos que chegássemos a uma solução.[33]

       Em minha opinião, qualquer método científico deve ter, como normas absolutas:

1) não desprezar dados experimentais confirmados;
2) não preencher lacunas teóricas com conceitos experimentalmente controvertidos;
3) não proteger teorias obsoletas, ainda que dotadas de elegância e beleza matemática;
4) não salvar equações que se mostraram incompatíveis com a experimentação, por mais que nos sejam simpáticas e/ou abrangentes;
5) tornar explícitas as metas a serem alcançadas em cada etapa da teorização;
6) propiciar revisões de resultados obtidos em etapas anteriores;
7) propiciar o desenvolvimento de teorias gerais (não ser limitante);
8) propiciar condições para que as teorias sejam passíveis a críticas;
9) dotar as teorias desenvolvidas de coerência interna;
10) abominar todo e qualquer tipo de preconceito.

       Os cientistas em geral concordam, defendem e enfatizam estas regras. Por motivos ignorados, raramente as seguem, como vimos no capítulo anterior.

       Em teorias de campo, o grande passo foi dado por Newton. Trezentos anos após, o derradeiro passo ainda está por ser dado; e a grande maioria dos físicos do nosso século não acredita nessa possibilidade. Constituem exceções importantes Schrödinger, De Broglie e Einstein, para os quais, citando Popper, "o cientista não deve abandonar a busca de leis universais, nem as tentativas de explicar causalmente qualquer tipo de evento". [op. cit. 22]

       Na verdade, sabemos muito sobre campos: em que age, como age e as conseqüências destas ações; e sabemos como produzí-los. Se deixarmos de lado o paradigma da ignorância, guiarmo-nos rigorosamente pelas normas apresentadas e focalizarmos a atenção para o agente causal elementar do campo, que é exatamente o que nos falta, chegaremos, sem dúvida alguma, nos alicerces de uma teoria de campo consistente. Vencida esta etapa, conhecidos os fundamentos, poderemos evoluir para o que seria, a rigor, a primeira fase da teoria, ou a fase dedutiva. A partir daí, e conhecendo-se a causa, ainda que por hipótese, poderemos estimar seus efeitos, chegando assim às equações de campo: esta é a segunda fase, ou a fase analítica da teoria, e que será o tema principal deste capítulo. Se a teoria for consistente, suas equações deverão nos revelar uma surpresa: além do conceito de campo não haverá qualquer conceito referente a partículas posto que, e por opção nossa, excluímos a causa ao definirmos o campo.

       Analisemos agora a ressalva feita no início do item: a propriedade que caracteriza um campo pode diferir se os objetos de prova considerados forem diferentes. Este inconveniente, em geral, pode e deve ser evitado. A força, por exemplo, nem sempre é uma boa propriedade para caracterizar um campo de forças pois seu valor somente é função da posição quando referido a um mesmo objeto de prova. No caso do campo elétrico o artefato adotado pela teoria clássica é simples: define-se a propriedade E como sendo a força por unidade de carga,

       em que esta última (q) é dada pela lei de Coulomb.

       O artefato será eficiente se, e somente se, todo elemento sensível ao campo puder ser imaginado como uma das esferas carregadas utilizadas na experiência de Coulomb. Uma partícula que não tenha essa propriedade, ou seja, que não possa ser pensada como uma carga elétrica puntiforme, apresentará, no campo considerado, um comportamento anômalo. Esta anomalia deve-se muito mais à má caracterização do campo do que a uma propriedade inerente à partícula (variáveis escondidas).

       Inúmeras foram as experiências efetuadas no século XX que mostraram um comportamento anômalo de elétrons quando submetidos a campos caracterizados pela expressão 4.1; e uma coletânea destas anomalias pode ser encontrada em qualquer livro de texto de física moderna.

       Existem, no entanto, algumas condições muito particulares nas quais o elétron simula um comportamento clássico, como se realmente possuísse uma carga q; e esta será a brecha que utilizaremos, no próximo item, para, com as hipóteses 1 a 4, penetrarmos no misterioso mundo das partículas elementares. Procuraremos interpretar estas raras situações experimentais no sentido de estabelecer o vínculo natural a nos levar à equação do elétron prevista na hipótese 3.

4.2 O campo de efeitos elétricos:

       Thomson (1897) e Millikan (1910), por métodos diferentes, verificaram que em um campo elétrico uniforme o elétron comporta-se de maneira similar a uma carga elétrica. Esta similaridade persuadiu-nos a considerar um campo elétrico uniforme como o local ideal para iniciarmos nossa análise.

       Pensemos então numa esfera condutora, com um raio muito grande, e eletricamente carregada. Esta carga elétrica produz um campo coulombiano E praticamente uniforme: é suficiente restringirmos o domínio do campo a pequenos volumes cujo eixo maior seja desprezível em relação ao raio da esfera. O raciocínio adotado é análogo ao efetuado quando dizemos que o campo gravitacional, nas proximidades da Terra, é praticamente uniforme.

       Os elétrons, nesta esfera, distribuem-se conforme estabelecido no Corolário 4: com seus eixos polares (aqueles definidos pelos vetores w's) perpendiculares à superfície esférica S. Sendo o raio da esfera muito grande, podemos representar os elétrons como mostrado na figura 6.

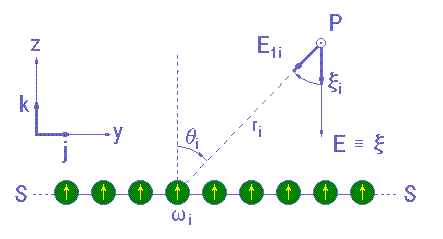
Figura 6: Comentários no texto.

       Em um ponto genérico P = (x,y,z) do domínio de E, e observando o Princípio da Superposição, podemos equacionar E da seguinte forma:

(4.2)

em que E_i é a contribuição do elétron i ao campo E no ponto P.

       Uma das possíveis soluções da equação 4.2 para o E_i do elétron i é dada pela equação de Coulomb:

Solução 1 (E i1):

(4.3)

onde K é uma constante de proporcionalidade intrinsecamente relacionada à definição de campo elétrico [O índice 1 está a indicar que esta é uma das possíveis soluções, no caso a solução 1, e poderia ser omitido sem prejuízos]. Esta solução, como vimos, mostrou-se incompatível com as experiências efetuadas no século XX.

       Outra solução, também compatível com a lei de Coulomb (em termos de carga elétrica) é:

Solução 2 (Ei2 ou x i):

(4.4)

com θ_i mostrado na figura 6. O campo x será aqui chamado "campo de efeitos elétricos" com a finalidade de distinguí-lo do clássico E que continuaremos chamando por campo elétrico. Para o caso atual, representado na figura 6, temos x = S x_i = E ou x = E, identidade esta que nem sempre será observada.

       Demonstraremos a seguir (ítens 4.2.1 a 4.3.1) que a solução 2 da equação 4.4 é realmente compatível com a lei de Coulomb.

4.2.1 O campo x de uma esfera condutora carregada:

       Do corolário 4 e da equação 4.4 concluímos: o campo de efeitos elétricos x_i de um elétron pertencente a uma superfície infinitesimal ds, de um condutor esférico eletricamente carregado, será:

(4.5)

       O significado das variáveis a, β e R) encontradas na equação 4.5 pode ser obtido do exame da figura 7:

Figura 7: Comentários no texto

       Seja dn o número de elétrons contidos em ds. Nestas condições, o campo de efeitos elétricos em P devido a ds será:

(4.6)

em que N = 4pR² dn/ds é o número total de elétrons componentes da carga elétrica considerada.

       Decorre da simetria do problema:

(4.7)

e da equação 4.6:

(4.8)

       Com a ajuda da figura 7 e sendo φ o ângulo azimutal, podemos observar as seguintes relações:

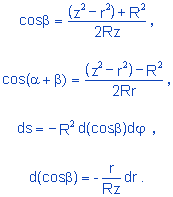(4.9)

       Substituindo 4.9 em 4.8 e simplificando, temos:

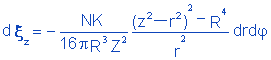(4.10)

Integrando 4.10 para z > r e z < R e observando 4.7, temos:

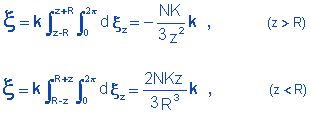
       Usando agora a notação convencional (r = distância de P ao centro da esfera = z) chegamos, finalmente, a:

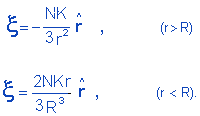(4.11)

4.3 A força eletrostática agindo sobre um elétron

       Quando pensamos no campo de efeitos elétricos x como um campo de forças, é necessário ter em mente que a sua ação, calculada pelos métodos rotineiros, leva-nos à força que age sobre um elétron e não sobre uma carga elétrica. É importante também observar que o campo x de um elétron (equação 4.4) é não coulombiano e não gaussiano (as linhas de campo não começam nem terminam no elétron). Apesar disso, e como vimos no item anterior, o campo x de uma carga elétrica esférica (equação 4.11) é do tipo coulombiano em seu exterior.

       Uma carga de prova q negativa, colocada num campo x uniforme, e equilibrada por seu peso, estará sujeita a uma força elétrica F tal que F = S F_iq. Neste caso F_iq é a força exercida por um elétron genérico i sobre a carga q, como mostrado na figura 8.

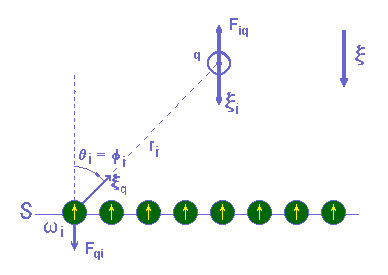
Figura 8: Comentários no texto

       O módulo de F é proporcional ao módulo do campo x, ou

F = C₁x

e graças ao Princípio da Superposição, válido para cargas coulombianas, podemos também escrever

       O campo x_q da carga q é gaussiano e dado pela lei de Coulomb para r > R (equação 4.11). Se x_q não for muito intenso relativamente a x, podemos desprezar os efeitos indutivos. Reunindo as relações de proporcionalidade, temos:

onde C₁, C₂ e C₃ são constantes. Resolvendo o sistema de equações 4.13 para F_iq, temos:

F_iq = C₄ x_qcosθ_i

ou, em notação vetorial:

F_iq = C₄ x_qcosθ_i k .

       A superfície S estará sujeita à reação - F = S F_iq. Parece razoável esperar que F_qi = - F_iq (ação e reação individualizada [34]). Aceitando-se esta igualdade, chegamos à expressão:

F_qi = - C₄x_qcosθ_ik .

       Será conveniente referir ao ângulo entre o vetor w de um elétron específico e a direção do campo a que este elétron está submetido pela letra grega f. No caso específico, sob consideração (figura 8), e tendo em vista que o campo x_q é coulombiano, este ângulo é igual a θ, definido pela equação 4.4 (f_i = θ_i). Nestas condições, a equação anterior pode ser escrita como:

F_qi = - C₄x_qcosf_ik .

       Generalizando, diremos que a força eletrostática que age sobre um elétron colocado num campo x, pode ser expressa por:

sendo f o ângulo entrex e v. (Lembrar que v é o versor de w.)

4.3.1 Força elétrica entre esferas condutoras carregadas:

       Seja um campo x, produzido por uma esfera condutora carregada, com centro em P = (0,0,0), e um elétron situado na superfície infinitesimal ds de outra esfera condutora com o centro localizado no ponto Q = (x,0,0).

Figure 9: Comentários no texto

       Este elétron estará sujeito a uma força elétrica F, dada pela expressão 4.14, a qual, adaptada às variáveis apresentadas na figura 9, será:

       Os efeitos indutivos foram desprezados, a exemplo do que se faz no estudo analítico da lei de Coulomb. Isto implica em se considerar os elétrons fixos e restritos a uma direção centrífuga. A força sobre ds será, então:

       As componentes dF_y and dF_z cancelam-se aos pares e, portanto,

       Com a ajuda da figura 9 chegamos às seguintes relações:

       Substituindo 4.18 em 4.16 e integrando conforme 4.17, e observando o valor de x dado por 4.11 para r > R, obtém-se:

       A expressão 4.19 nada mais é que a lei de Coulomb expressa em termos dos números de elétrons N e N' contidos nas cargas Q e Q'.

	Indice deste Artigo
Retornar		Avançar

DHTML Menu By Milonic JavaScript