5.1 Equações fundamentais:

       Duas equações, dentre as apresentadas no item 4, são fundamentais para que possamos prosseguir com nossa análise. A primeira fornece-nos o campo de efeitos elétricos produzido por um elétron (relação causa-campo):

enquanto que a segunda traduz, em termos de força, o comportamento eletrostático de um elétron colocado em um campo de efeitos elétricos causado por outro ou mais do que um elétron (relação campo-efeito):

       É importante entender e saber distinguir o significado de ambos os xs (ou vs) das equações 5.1 e 5.2. Na primeira das equações, x evidencia o campo gerado por um elétron; na segunda, x significa o campo que age sobre o elétron em consideração. Deve-se notar também que estamos seguindo a convenção adotada na hipótese 1: v é um vetor unitário tal que w = Kv

5.2 Os ângulos q e f:

       Seja w um vetor que define um elétron e x o campo de efeitos elétricos produzido pelo mesmo em um ponto P de uma reta r que contém o elétron. Nestas condições θ será o ângulo medido no sentido horário, iniciando em w e terminando em r.

       Seja agora w o vetor que define um outro elétron situado num campo x. Nestas condições, f será o ângulo medido no sentido horário, iniciando em w e terminando em x

       Finalmente, sejam w₁ e w₂ dois vetores que definem os elétrons 1 e 2. A figura 10 ilustra, através de θ₁ e f₂ o que foi comentado nos dois parágrafos precedentes. Na figura estão também representados os ângulos conjugados de θ₂ e f₁, identificados por um traço superior (ângulos conjugados são aqueles cuja soma é igual a 2p). Ao se trabalhar com as equações 5.1 e 5.2 é indiferente utilizar um determinado ângulo ou o seu conjugado pois os cosenos de ângulos conjugados são iguais.

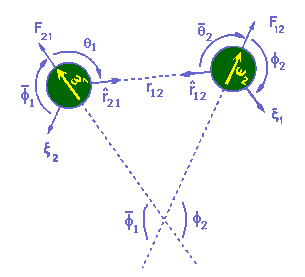
Figura 10: Comentários no texto

5.3 O produto vetorial interno:

       Definiremos o produto vetorial interno de dois vetores u e v, a ser denotado por uÄv, ao vetor cujo módulo é o mesmo do produto interno (ou escalar) entre os dois vetores e cuja direção é a do segundo vetor (no caso, v). Temos então:

devendo-se notar que uÄv ¹ vÄu.

       Comparando 5.2 e 5.3 e observando a definição para f apresentada no item anterior, concluímos que

5.4 O translacional de um vetor A:

       O estudo matemático de campos é facilitado pelo uso de um grupo de operadores diferenciais de vetores tais como o gradiente, a divergência e o rotacional.

       O conceito de rotacional está intimamente relacionado ao de produto vetorial:

u × A Û Ñ × A .

       Neste relacionamento, destacam-se algumas características elementares comuns a ambos produtos; por exemplo, o vetor resultante é perpendicular a A em todos os pontos do domínio de A. No entanto, no primeiro caso (produto vetorial) o vetor resultante u×A tem uma direção que depende exclusivamente das direções de u e A no ponto considerado e independe do valor de A em qualquer outro ponto de seu domínio; e esta direção é, por conveniências físico-matemáticas (por definição) perpendicular tanto à direção  de u quanto à de A. Já no segundo caso (rotacional) realçam as seguintes propriedades importantes:

1. Ñ é um operador diferencial que, conquanto tenha algumas características matemáticas que o identifiquem algebricamente a um vetor, não é um vetor e, portanto, não tem uma direção definida.
2. Definido Ñ e conhecido o campo A, não nos resta nenhum grau de liberdade que nos permita escolher uma direção para Ñ´A.
3. A direção de Ñ´A depende do comportamento de A nas vizinhanças do ponto considerado;
4. A existência de Ñ´A como campo vetorial não é intuitiva mas apóia-se na obediência a normas físico-matemáticas rígidas [35] [36].
5. Por ser um operador diferencial, Ñ´ opera satisfazendo as regras de diferenciação parcial, incluindo a diferenciação de um produto.

       De um modo geral, o rotacional de um campo vetorial está relacionado com as propriedades de rotação do campo [37], podendo-se estimar grosseiramente o seu valor em um campo mapeado pela observação da circuitação no contorno de um pequeno elemento de área. Trata-se de uma espécie de derivação colateral e envolve a taxa de variação de A_x segundo y ou z [38].

       Iremos agora expandir estas idéias para o conceito de produto vetorial interno definido em 5.3.

       Em primeiro lugar deve ser observado que, por conveniência, escolhemos uma direção para o produto vetorial interno, uÄA, que coincide com a direção de A:

uÄA = (u.A) Â

       Neste caso, ao contrário do conceito clássico de produto vetorial, a direção do vetor resultante é independente da direção do vetor u. Se quisermos encontrar um operador que promova, num campo A, uma diferenciação vetorial interna, tal que possamos encontrar um relacionamento do tipo

uÄA Û ÑÄA,

o vetor resultante deverá ter uma direção independente da diferenciação Ñ, e ser do tipo

       O produto vetorial interno de Ñ por A, conforme expresso em 5.5, será aqui chamado por translacional de A. Esta denominação justifica-se haja vista que o translacional de um campo vetorial, em alguns casos importantes, lembra a derivada direcional deste campo segundo as linhas de campo.

	Indice deste Artigo
Retornar		Avançar

DHTML Menu By Milonic JavaScript