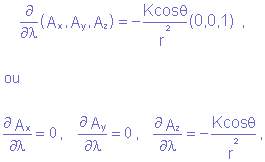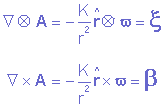6.1 O campo A:

       Como uma partícula elementar lê um campo a ponto de reagir a seu conteúdo. Pensemos em um campo de forças elétrico, magnético ou gravitacional. Estes nada mais são do que campos de efeitos, ou regiões do espaço dotadas de particularidades tais que produzem efeitos mensuráveis sobre determinados objetos. Existe, portanto, um potencial local e específico, o qual deve-se a uma propriedade física variável, continuamente, de ponto a ponto. Qualquer partícula de dimensões finitas, desde que sensível a esta propriedade local, reage ao campo, como um objeto macroscópico frente a uma ventania.

       Um campo elétrico x pode sempre ser pensado como uma derivada específica de outro campo vetorial A, desde que A comporte matematicamente esta função. Suponhamos então que exista um campo A que possua, em cada ponto de seu domínio, todas as derivadas direcionais e, portanto, seja dotado de linhas de campo regulares. Numa primeira tentativa de satisfazer a hipótese 4 (H-4) podemos imaginar como deveria ser o campo A de um elétron tal que

em que representa a derivada de linha de A com relação ao comprimento de arco l ou, simplesmente, a derivada curvilínea segundo as linhas de campo l de A no ponto considerado. Decorre então de 5.1 que

equação esta que, para um referencial cartesiano convenientemente escolhido (v // k), transforma-se em

       Conseqüentemente, A_x = C₁ e A_y = C₂, com C₁ e C₂ constantes. Mas sendo A um vetor que retrata, de alguma forma, o conteúdo local de informações eletromagnéticas em trânsito e emitidas pelo elétron (vide H-2 e H-3), devemos ter

e, portanto, C₁ = C₂ = 0. Nestas condições, l coincide com o eixo z e a expressão para A_z tem por solução A_z = K/r + C₃ a qual, por motivos análogos aos discutidos acima para C₁ e C₂, tem C₃ = 0. A solução de 6.2 será então, com w definido em H-1:

equação esta que concorda com H-3 e, como será visto a seguir, com H-4, sendo portanto a procurada equação do elétron em repouso.

       Calculando, agora, o translacional e o rotacional de A, dado por 6.3, chegamos facilmente às expressões:

em que b satisfaz a lei de Biot-Savart e nada mais é do que o campo de efeitos magnéticos de um elétron em repouso. Consequentemente, A, definido por 6.3, satisfaz integralmente as hipóteses básicas.

       É interessante notar que partimos da lei de Coulomb, para uma esfera de raio infinito, e chegamos na lei de Biot-Savart; mais interessante ainda é verificar a reversibilidade matemática desta via teórica de raciocínio: é possível partir da lei de Biot-Savart e chegar na lei de Coulomb. Com efeito, estas leis são matematicamente equivalentes e as equações 6.3 e 6.4 operam a transformação de uma em outra.

6.2 As equações fundamentais da eletromagnetostática:

       O campo de efeitos eletromagnéticos de um elétron em repouso resume-se no sistema de equações

com A dado por 6.3. Tendo em vista que os campos x e b são aditivos (princípio da superposição) e o translacional, ao contrário do rotacional, não obedece à propriedade distributiva, o sistema 6.5 não é generalizável para quaisquer campos eletromagnéticos. Em outras palavras, o campo eletromagnético (x,b) de uma população de elétrons não pode, via de regra, ser expresso em função de um único vetor A. Neste caso, temos então:

       A equação de efeitos correspondente é

com x e b calculados por 6.6. F_j é a força eletromagnética que age sobre um elétron j situado em um campo A estacionário. K₁ e K₂ são constantes determináveis. As equações 6.5 e 6.7 praticamente encerram, em seus conteúdos, toda a eletromagnetostática, com a exceção de um fator importante relacionado ao campo de indução t mencionado no item 3.3.

6.3 O escalar do campo eletromagnético:

       É possível [39] considerar o campo eletromagnético de um eletron através de uma função escalar φ dada por

Para tanto é suficiente definir x e b através das expressões

e observar que a função φ, definida em 6.8, apresenta as seguintes propriedades

       Demonstra-se assim facilmente que

e, consequentemente, a compatibilidade entre 6.8 e 6.3.

6.4 As informações eletromagnéticas (i.e.m.):

       As equações 6.9 mostram-nos que o campo eletromagnético (x,b) do elétron pode ser descrito em termos do gradiente de uma função de posição φ. Podemos então conjecturar sobre a existência real de alguma coisa emitida pelo elétron e chamá-la informação eletromagnética (i.e.m.). A equação 6.8 sugere mais: uma vez emitidas, as i.e.m são conservadas. Em outras palavras, o elétron é uma fonte emissora de i.e.m. e o fluxo de i.e.m. ao cruzar uma superfície identifica-se com o fluxo de um campo vetorial h expresso por

       Está implícito nestas considerações que h é do tipo h = ρc, sendo ρ um invariante que representa a densidade local de i.e.m. e c é a velocidade de propagação das i.e.m. em um sistema referencial apropriado.

	Indice deste Artigo
Retornar		Avançar

DHTML Menu By Milonic JavaScript