3.1. Evolução Histórica:

       Conquanto existam inúmeras experiências realizadas no século XX e capazes de justificar as hipóteses apresentadas, convém, a bem da clareza, seguir a evolução histórica do eletromagnetismo, apoiando-as em conceitos fundamentais. Com isso virão à tona as bases em que se sustentam alguns paradigmas e o leitor julgará, por si próprio, se deve ou não continuar aceitando-os como verdades absolutas.

       Sthephen Gray, em 1729, foi o primeiro a constatar que a virtude elétrica podia ser transferida de um corpo a outro; Charles François Du Fay (1678-1739) mostrou que, sem um isolamento adequado, tal virtude fugia dos corpos; e Priestley (1733-1804) verificou que a eletricidade se distribuía do lado externo de um vaso metálico, ou seja, fugindo de seu interior [12]. Entre 1784 e 1789, Coulomb publicou sua teoria. Entre as hipóteses (vide as demais logo a seguir), uma relacionava-se a este efeito fuga:

a) Num corpo condutor eletrizado o fluido elétrico espalha-se à superfície mas não penetra no interior do corpo [13].

      Este fato foi definitivamente comprovado pelas experiências de Faraday e, desde então, sempre corroborado, cada vez com melhor precisão. Paralelamente a essas descobertas, outras propriedades foram confirmadas para os fluidos coulombianos:

      b) Os corpos eletrizados por um mesmo fluido repelem-se, os eletrizados por fluidos diferentes, atraem-se;
     c) Essas atrações ou repulsões produzem-se na razão direta das densidades ou forças dos fluidos elétricos e na razão inversa do quadrado das distâncias [13].

      Hoje não há mais porque se pensar em fluidos elétricos. Inúmeros autores, a começar por Faraday em 1833, com a lei da eletrólise, constataram, por métodos vários, a natureza atômica da eletricidade. Podemos então dizer que os elétrons em excesso em um meio condutor caminham "até o limite de suas possibilidades", ou seja, até a periferia do condutor, aí permanecendo. Inicialmente, num estágio quase instantâneo, temos um amontoado de "elétrons em fuga"; após o equilíbrio temos uma carga elétrica.

      A lei de Coulomb (hipótese c acima) relaciona-se a cargas elétricas retratando uma polarização espacial radial. Se o elétron, como visto em H-1, é uma partícula vetorial e se, conforme implícito em H-2, o espaço, na ausência de elétrons, é isotrópico, segue-se de C-2 e C-3 que

      O estudo quantitativo dos fenômenos elétricos, até 1800, restringiu-se praticamente a estados de equilíbrio, dada a quase instantaneidade de seu estabelecimento. Com o advento da célula voltáica, um novo horizonte se abriu possibilitando a obtenção de leis de estado estacionário. Em 1820 Hans Christian Oersted verificou que uma bússola sofria uma deflexão quando colocada nas vizinhanças de um fio condutor [14] e esta foi talvez a maior descoberta da história do eletromagnetismo. Em menos de um mês Biot e Savart mediram a força exercida por uma corrente elétrica sobre o polo de uma agulha magnetizada [15] e de tais medições Laplace deduz a lei de Biot-Savart para um elemento de corrente percorrido por uma corrente i,

sendo dF o elemento de força agindo sobre um polo norte de um imã igual à unidade e j o ângulo entre os vetores r e ds. A lei de Biot-Savart, em sua forma diferencial (equação 3.1) tem aspectos que a tornam análoga à lei de Coulomb, apenas que refletindo o comportamento de elétrons em fuga permanente, ou seja, elementos de corrente com intensidade i constante (estado estacionário). Na forma integral é conhecida como lei de Ampère-Laplace [16].

      Não é fácil entender o que seja um elemento de corrente ids. Por um lado, sintetiza o eletromagnetismo em sua expressão mais simples; por outro, não existe, a não ser como produto da genialidade humana. É algo hipotético e puramente matemático em suas origens: é uma corrente que flui do nada para o nada e que, ao passar pelo mundo real, através de nada mais do que um ponto material, deixa-nos uma equação a qual, integrada aos infinitos ids semelhantes, resulta numa lei circuital, relacionada a um circuito real. Trata-se da mais sutil e engenhosa aplicação do cálculo diferencial efetuada após Newton.

      Qualquer semelhança entre um elemento de corrente ids e um elétron em movimento é mera coincidência posto que no decorrer do tempo o elétron vai embora e o elemento abstrato permanece. De qualquer forma, é possível, como veremos, caracterizar o elemento de corrente de forma não tão abstrata e, assim sendo, concluir:

      É de se notar o contraste entre C-1 e C-5.

      O Corolário 5 não é impositivo mas, sim, abre-nos um caminho. Caminho este que, respeitadas as restrições que comporta, mostrar-se-á de grande valia.

      Seja então um ponto P do espaço, arbitrário porém constante, e um elemento ids fixo, ou seja, constante em s e ds, de um circuito de corrente elétrica. Aceitando como válida a lei de Biot-Savart, 3.1, podemos escrever:

em que Y = senj/r² = constante. Portando, dado i, dF estará definido. Lembrando ainda que, por definição,

e substituindo 3.3 em 3.2, temos

(3.4)

ou

      Duas questões emergem: 1) O que significam v e dq? 2) A segunda igualdade, em 3.4, está correta? Esta transformação é permitida?

      Utilizando as palavras de Spiegel [17], "dado dt determinamos dq mediante 3.3,isto é, dq é uma variável dependente determinada a partir da variável independente dt para um dado t". Ou seja, dq pode assumir qualquer valor que queiramos, desde que se escolha convenientemente dt. E, assim sendo, a transformação em discussão é permitida desde que as diferenciais estejam "amarradas" ou desde que v = ds/dt seja tal que a dependência entre dq e dt seja respeitada. Convém então escolher para dq um valor dq_e relacionado ao número de elétrons contidos em ds e responsáveis pelo campo dF; dq_e é então a carga eletrolítica do circuito medida num tempo dt' em que a mesma atravessa ds (notar que trata-se de um valor de natureza teórica e, por si só, indeterminado). Com isso é fácil verificar que v adquire a característica de velocidade de arraste v_a (v_a = ds/dt') de dq_e na direção ds (v tem a dimensão de velocidade). Nestas condições a expressão 3.5 torna-se

3.2. Teorias Microscópicas:

      O relacionamento causa(dq_e)-campo(dF) da expressão 3.6, aliado à indeterminação operacional de dq_e, fomenta a teorização. Admitamos, então, que o elemento de corrente ids pertença a um condutor öhmico e que possamos variar a corrente i, conservando ds constante. As conseqüências imediatas são dadas pela equação 3.2: dF é proporcional a i. Ora, se dF varia com i, então v_a e/ou dq_e, pela equação 3.6, devem também variar. Três são as possibilidades teóricas:

a) dq_e é constante e dF depende apenas de v_a.
b) v_a é constante e dF depende apenas de dq_e.
c) dq_e e v_a variam com i.

      Discutiremos apenas a primeira possibilidade pois esta é a base da teoria de Drude (1900) e Lorentz (1909) da condução elétrica apoiada no modelo dos elétrons livres ou dos "fluidos elétricos incompressíveis". [18].

      Segundo o modelo dos fluidos elétricos incompressíveis existe, num condutor, um gás de elétrons que, por si só, não tem nenhum efeito sobre a intensidade do campo eletromagnético, posto que as cargas negativas são compensadas pelas positivas. Estando o condutor imerso num campo elétrico, existiria um arraste das cargas móveis (elétrons do gás) sendo a velocidade deste arraste, v_a, a única responsável pela origem do campo magnético. O fator dq_e da expressão 3.6 teria, como único efeito, modular dF, ou seja, quanto mais elétrons com velocidade v_a, maior seria o campo magnético que originaria; e dq_e depende exclusivamente da estrutura do material condutor. Segundo Tipler [19]:

Este modelo prevê, com sucesso, a lei de Ohm e relaciona a condutividade e a resistividade ao movimento dos elétrons livres em um condutor. Esta teoria clássica é útil no entendimento da condução, embora tenha sido substituída por uma teoria mais moderna, baseada na mecânica quântica.

      Em outras palavras: a teoria fracassou, necessitando algumas correções, efetuadas ad hoc, que a tornassem compatível com os achados experimentais; e qualquer que seja a interpretação dada pela mecânica quântica ao fenômeno em si, a verdade é que a possibilidade (a) ficou descartada pela experiência.

      Podemos então deixar este tópico com uma certeza garantida pela experimentação: o campo magnético de um elemento de corrente depende da carga eletrolítica dq_e contida nesse elemento e, consequentemente, do número de elétrons que a determinam. Este fato, aliado à simetria cilíndrica do campo, leva-nos, por raciocínio idêntico ao utilizado para a obtenção de C-4, ao seguinte corolário:

3.3 Propriedades Eletromagnéticas do Elétron:

      À luz das hipóteses 1 a 4 e dos corolários 1 a 6 podemos fazer uma primeira idéia do que seja uma carga elétrica ou uma corrente elétrica. A figura 2 é uma imagem dessa idéia, sobressaindo, na mesma, que os efeitos elétricos de um elétron estão relacionados à sua região polar e os efeitos magnéticos à região equatorial.

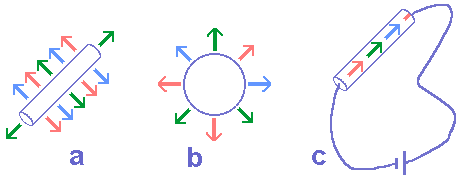
Figura 2: a) Elétrons estacionários em um condutor cilíndrico;
             b) elétrons estacionários em um condutor esférico;
       c) elétrons em movimento em um fio condutor.

      A existência de dois tipos distintos de carga (positiva e negativa) dotadas de partículas elementares diferentes (respectivamente próton e elétron) e mais, cada uma gerando um campo diverso do outro (respectivamente centrífugo e centrípeto), nos permite ir além e concluir: os elétrons (prótons) são dotados de polos distintos ¾digamos, frente F e dorso D¾ e quando entram na constituição de uma carga elétrica direcionam apenas um destes polos ¾digamos, o polo F ¾ para o exterior. A razão desta preferência direcional será discutida oportunamente.

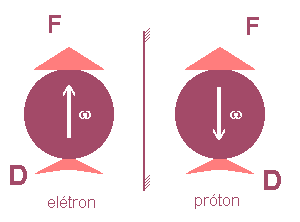
Figura 3: Simetria quiral elétron-próton.
(consideradas apenas as propriedades eletromagnéticas).
O polo F é aquele que, numa carga elétrica, dirige-se para fora.

      Os polos direcionalmente afins, de prótons e elétrons, são funcionalmente opostos. Em outras palavras: as partículas elementares do eletromagnetismo têm uma simetria quiral clássica (figura 3). A figura 4 fornece um primeiro esboço do que poderíamos chamar um elétron físico, achando-se também representado um campo de natureza mista. A rigor, não existem dois campos físicos mas apenas um, o campo eletromagnético A (corolário 2), que se manifesta por três, e não apenas dois, efeitos eletromagnéticos. A cada um destes efeitos é possível associar-se um campo secundário: o campo de efeitos elétricos x, o campo de efeitos magnéticos b e o campo de indução t, ou de efeitos indutivos. O termo campo de efeitos, adotado a estes campos secundários, realça a susceptibilidade à observação através de elementos de prova e, consequentemente, à mensuração. Nos ítens anteriores já se fez menção aos campos x e b, ainda que de passagem e sem a preocupação de definí-los. Vejamos, por ora, o que seja, em linhas bem gerais, o campo de indução t.

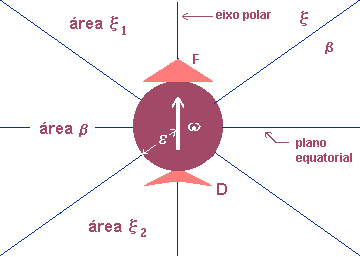
Figura 4: Um primeiro esboço do elétron físico.
x₁ e x ₂: regiões predominantemente elétricas.
b: região predominantemente magnética.
ε: raio do elétron (hipotético).

      Um corpo neutro imerso em um campo eletromagnético A, dependendo de sua estrutura e do campo considerado, pode eventualmente comportar-se ora como carga elétrica, ora como carga magnética, fenômeno este conhecido desde a antiguidade. O corpo eletriza-se ou magnetiza-se, dependendo das características do campo original. Obviamente, a indução retrata uma acomodação de partículas elementares, fenômeno este muito parecido com o que descrevemos no item 3.1 como elétrons em fuga. Aqui, as partículas movem-se em obediência ao campo externo; lá os elétrons fugiam em obediência ao campo provocado pelos seus semelhantes. Esta fuga, sem sombra de dúvida, é direcionada. Como então um campo de força, seja ele elétrico, seja magnético, pode direcionar uma partícula polar? Seria necessário, acoplado a esse campo, um campo de torques! E é este o campo que mantém os elétrons direcionados em uma carga elétrica ou corrente elétrica, conforme exposto na figura 2.

3.4 Pontos Críticos nas Teorias Clássicas

      Existe, na teoria de Maxwell, inúmeras lacunas conceituais responsáveis pela crença em teorias outras que, conquanto clássicas em origem, acabam colocando o eletromagnetismo clássico em xeque. Aparentemente inocentes e independentes, concebidas em uma fase de muitas dúvidas sobre a estrutura íntima da matéria (entre 1895 e 1915), têm em comum um ponto de convergência: todas elas desafiam a experimentação. Por inúmeras vezes mostraram-se incompatíveis com a lógica clássica e sobreviveram unicamente porque preenchiam as lacunas apontadas. Em conjunto, tecem o terreno propício sobre o qual viria a se apoiar a física moderna. Ainda que, por ora, nos falte condições para explorá-las em profundidade, vale a pena citar já três destas teorias, visto estarem em flagrante discordância com a idéia de elétron aqui concebida: a) a teoria dos elétrons livres, para condutores, já comentada; b) a teoria dos dipolos elétricos, para dielétricos; e c) a idéia teórica de que um elétron acelerado sempre emite energia radiante, esteio da concepção das órbitas permitidas de Bohr, ou seja, das regiões onde o elétron "está autorizado" a desrespeitar a regra imposta. Começaremos por esta última.

3.4.1 As Órbitas Permitidas

      Após a experiência de Geiger e Marsden's (1909) sobre o espalhamento de partículas alfa por uma fina folha de ouro, Rutherford propôs um modelo de átomo nucleado, deixando pouco espaço para dúvidas em relação a sua validade [20]. De posse do modelo de Rutherford e de medidas espectroscópicas relativas a radiações eletromagnéticas emitidas por átomos e decifradas a partir de 1885, Bohr (1913) desenvolveu a teoria Sobre a constituição de átomos e moléculas [21]. As hipóteses assumidas por Bohr foram posteriormente sintetizadas em quatro postulados básicos. Dois destes, extraídos de Eisberg e Resnick [20], dizem:

      O P3B sempre foi o mais questionado, ainda que menos contestável que o P1B, posto que traduz em palavras o que é observado no laboratório. O mesno não se pode dizer do P1B: nenhuma experiência até hoje demonstrou, de forma incontestável, que as interações elétron-núcleo são coulombianas. Pelo contrário, são incontáveis as experiências efetuadas no século XX que retratam uma única verdade: o elétron desconhece a lei de Coulomb.

      Em 1911, dois anos antes da publicação da teoria de Bohr, Kamerlingh Onnes descobriu um fenômeno assaz interessante: a supercondutividade do mercúrio. Em um supercondutor, como foi demonstrado mais tarde, circulam correntes que persistem durante anos sem que se possa detectar seus decaimentos [20]. Portanto, num supercondutor o elétron também percorre trajetórias onde lhe é permitido desrespeitar a teoria eletromagnética clássica. Até 1957 este fenômeno permaneceu quase sem explicação alguma. A coletividade científica assimilou bem a permissividade absurda, porém o maior empecilho para a teorização era a incompatibilidade entre o fenômeno e a teoria da condução elétrica de Drude e Lorentz, já comentada. Em 1957 Bardeen, Cooper e Schrieffer (BCS) decidiram ignorar a teoria dos elétrons livres, propondo um modelo concordante com os resultados experimentais. A teoria BCS ganhou grande repercussão e, devido a seu sucesso, passou-se a admitir concomitantemente: o P3B é verdadeiro, a teoria BCS é verdadeira, as equações de Maxwell são verdadeiras e a teoria dos elétrons livres é verdadeira. Em meio a tantas verdades incompatíveis, quem sofreu foi a metodologia científica. Enfim, algo é falso: a lógica de Popper [22].

      A discordância sobre o tema não se restringe ao domínio da física. Os híbridos de ressonância, da química, constituem um exemplo no qual destaca-se a estrutura do benzeno. Aí, seis elétrons deslocalizados circulam, indiferentes às previsões teóricas, tal e qual os elétrons de um supercondutor excitado, conferindo ao benzeno "uma estabilidade de difícil explicação" [23]. As reações de oxidação e redução também são problemáticas: ocorrem em duas versões termodinâmicas e, ao que parece, as previsões da teoria de Maxwell, tal e qual nos condutores, funcionam bem apenas na versão irreversível. Neste terreno semi-obscuro da química realça o "Modelo de Intersecção de Estados" (MIE) desenvolvido por Formosinho e Varandas [24]; se bem o entendi, o MIE parece sugerir, no caso das reações de oxidação e redução, um estado intermediário em que os elétrons transitariam por macro-órbitas efêmeras e "permitidas", ou seja, sem irradiar energia.

      Há em biofísica dois processos metabólicos de importância vital: a respiração celular e a fotossíntese. Cadeias de transporte de elétrons, indiferentes aos postulados da física clássica, acoplam-se a sistemas que armazenam a energia que deveria ser irradiada pelos elétrons aí desacelarados. Este fenômeno foi expresso por Szent Györgi, quando passou por Princeton (New Jersey, EUA), com as seguintes palavras:

      O que há de notável no caso é que o elétron sabe exatamente o que tem de fazer. Assim, esse pequeno elétron conhece uma coisa que todos os sábios de Princeton ignoram, e que só pode ser uma coisa muito simples [25].

      A energia armazenada durante esta desaceleração é convertida em energia química através da fosforilação oxidativa. A fosforilação oxidativa, segundo Peter Dennins Mitchell, processa-se graças à mediação de um sistema enzimático polarizado, localizado na membrana interna das mitocôndrias e que permite o transporte de prótons através da membrana, em obediência a um gradiente protonmotriz [26]; e os prótons, aí acelerados, deixam a sua energia não irradiada com o ATP. Existe, portanto, uma trajetória enzimática onde os prótons, a exemplo dos elétrons de Bohr, estão autorizados a desrespeitar a regra clássica. É de se notar que, em todos os exemplos acima mencionados, as trajetórias permitidas são regiões de confinamento adiabático, o que se traduz no caráter reversível dos processos que os utilizam.

      A concepção de átomo como sistema planetário, baseada no modelo de Rutherford, ao mesmo tempo em que se tornou a única hipótese plausível, transformou-se numa assombração para os físicos da época. A saída para o dilema foi encontrada por Bohr através de seus outros postulados (P2B e P4B de acordo com a numeração de Eisberg). Estes postulados são estratégicos no sentido de que estão em acordo com a experimentação e, ao mesmo tempo, mascaram a coexistência absurda entre os outros dois postulados (P1B e P3B acima enunciados). Com efeito, no P2B Bohr refere-se à infinidade de órbitas possíveis para um elétron num átomo, segundo a mecânica clássica. Ora, a mecânica clássica somente entra em ação a partir do momento em que as forças de interação elétron-próton forem definidas; e, como vimos, se estas interações forem coulombianas, o P3B é falso, ou vice-versa. Consequentemente, e até o momento, a mecânica clássica nada nos garante sobre o possível número de órbitas.

      Resumindo, qualquer que seja o relacionamento próton-elétron ou núcleo-elétrons, a verdade é que o conjunto resultante deve ser bem mais complexo do que um par de estrelas binárias, ou ainda um sistema planetário mantido em estado estacionário pela inércia e pelas interações gravitacionais.

3.4.2. A Teoria dos Dipolos Elétricos

      Vejamos agora alguma coisa sobre a teoria dos dipolos elétricos. Sabemos que os condutores, quando submetidos a uma força eletromotriz, tornam-se sede de uma corrente elétrica; mas, se estiverem isolados da fonte do campo, como na figura 5a, a corrente extingue-se tão logo a separação de cargas atinja determinado limiar. Faraday, em seus estudos com capacitores, verificou que os dielétricos, conquanto não conduzam correntes elétricas, manifestam um comportamento qualitativamente semelhante. Estes materiais resistem parcialmente à penetração do campo elétrico em seu interior, fenômeno este que lembra, em alguns aspectos, o empuxo de Arquimedes que opõe-se ao campo gravitacional.

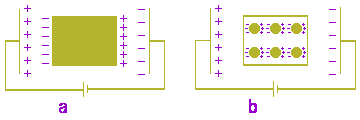
Figura 5: Comentários no texto

      No final da era dos fluidos elétricos surgiu uma teoria promissora que admitia o dielétrico constituído por pequenas esferas condutoras imersas num meio isolante [27]; o fenômeno complexo pôde, assim, ser reduzido a uma somatória de efeitos simples, conforme mostrado na figura 5b. A teoria, dentro dos limites a que se propõe, é perfeita e, embora seja uma teoria representacional, podemos, utilizando a linguagem de Mario Bunge [28], considerá-la de baixo risco pois explica o observável (caráter fenomenológico ou behaviorista) através de um mecanismo interno (caráter representacional) de importância secundária. Em outras palavras, o modelo microscópico (figura 5b) em nada modifica o modelo que lhe deu origem (figura 5a).

      Nos primórdios da era atômica a situação não era mais esta: as esferas condutoras foram identificadas aos átomos de Thomson e o meio isolante ao éter que os entremeava. O caráter representacional da teoria ganhou em importância, o que a transformou em uma teoria de alto risco.

      Após a identificação do caráter corpuscular dos raios catódicos, corpúsculos estes que posteriormente receberam da denominação de elétrons, Thomson sugeriu que a carga positiva de um átomo pudesse estar distribuída uniformemente em uma esfera, com os corpúsculos negativos situados no interior da carga positiva [27]. Ou, como citado por Tipler [29], Thomson considerou o átomo como um fluido carregado positivamente e com elétrons mergulhados em uma configuração estável e de maneira a tornar o conjunto neutro. Devido à repulsão mútua, segundo Eisberg e al. [op.cit. in 20], os elétrons estariam uniformemente distribuídos na esfera de carga positiva, de onde a denominação "modelo em pudim de passas"; e quando da excitação do átomo, os elétrons vibrariam em torno de suas posições de equilíbrio, o que explicava qualitativamente a emissão de radiação eletromagnética.

      A teoria dos elétrons livres desenvolveu-se sob este clima (1900 a 1909) e não é difícil recuperar sua lógica: se os fluidos positivos dos átomos de Thomson, de alguma forma, intercomunicam-se ou constituem uma massa amorfa única, os elétrons aí localizados estão praticamente livres, ainda que presos à massa como um todo. Um material onde tal ocorre seria um condutor; caso contrário, um dielétrico. A idéia de fluido persistia mas já se pensava em partículas negativas. E os físicos estavam a um passo de imaginar os modelos apresentados nas figuras 5a e 5b como dipolos elétricos posto que em muito assemelhavam-se ao conjunto macroscópico de duas cargas coulombianas de mesma intensidade e sinais contrários.

      A noção de dipolo elétrico estático surgiu, germinando também, em tão fértil terreno, um conceito aparentado: o dipolo elétrico dinâmico. As experiências de Hertz e o modelo de Thomson favoreceram esta concepção. Com efeito, o radio-transmissor e o radio-receptor utilizados por Hertz são chamados antenas dipolos; e o modelo em pudim de passas, com elétrons vibrando em torno de uma posição de equilíbrio, em muito assemelha-se a estas antenas. Tanto assim é que Planck (1900), em sua teoria de emissão de radiação térmica, afirma: a superfície emissora contém elétrons ligados a pontos fixos através de forças que obedecem à lei de Hooke [30].

      Enquanto o modelo de Thomson se autojustificou, a teoria dos elétrons livres representou um ramo desta árvore e a idéia de dipolos microscópicos, em outro de seus ramos, floresceu. Não obstante, as restrições experimentais a que o modelo devia acoplar-se eram, sem dúvida alguma, excessivas e Thomson, apesar de ter realizado cálculos matemáticos elaborados, foi incapaz de obter concordância com a experimentação [op. cit in 29]. A partir da análise conclusiva de Rutherford sobre a natureza nucleada do átomo, a árvore foi derrubada; mas seus ramos já haviam frutificado. A polarização elétrica em dielétricos, bem como a emissão de radiação, passaram então a ser explicadas por uma teoria agora puramente fenomenológica; de baixo risco, é verdade, porém embebida num abstracionismo muito intenso: os dipolos atômicos conservaram pouco das características físicas e muito das características matemáticas.

      Um átomo de hidrogênio clássico (modelo de Rutherford) possui um vetor momento de dipolo p que varia com o tempo. Segundo Goldenberg [31] ele deveria gerar um campo elétrico variável no tempo e, portanto, emitir radiação eletromagnética. Esta conclusão, conquanto classicamente legítima, pressupõe a inexistência de campos elétricos estacionários variáveis no tempo, suposição esta não apoiada na experimentação.

      A ausência desta radiação no átomo normal de hidrogênio foi um dos grandes paradoxos da física quântica primitiva [31]; paradoxo este que somente foi "resolvido" através da aceitação de um elétron ondulatório: a estrutura eletrönica de átomos e moléculas pode ser representada por uma única nuvem de cargas negativas de densidade variando continuamente [31]. Imagem esta que lembra o modelo de Thomson às avessas: uma nuvem (fluido) carregada negativamente, com um núcleo puntiforme e positivo situado no interior da carga negativa. Em outras palavras, o dipolo elétrico, como atualmente concebido, é incompatível com o eletromagnetismo clássico; ou melhor dizendo, os princípios em que se apóia o eletromagnetismo clássico são inadequados para explicar o paradoxo que gerou.

	Indice deste Artigo
Retornar		Avançar

DHTML Menu By Milonic JavaScript