7.1 O sistema inercial:

       Quando uma carga elétrica coulombiana passa de um estado de repouso para outro em movimento retilíneo e uniforme, ela emite, durante a fase de aceleração, uma aura que delimita dois universos:

Figura 11: Campo elétrico de uma
carga em movimento

1. Um universo interior, que contém o campo da carga já adaptado ao seu movimento inercial ¾ neste universo tudo se passa como se a carga estivesse em repouso no referencial em movimento uniforme.
2. Outro universo, exterior, que contém o campo da carga em repouso no referencial inercial inicial.

       A aura consiste de uma membrana móvel de espessura finita, sede de um campo mutante ou do que nos acostumamos a chamar por radiação eletromagnética. Esta aura, ao atravessar uma região do espaço, a uma determinada velocidade, promove a transformação de um campo inercial (aquele da carga em repouso) em outro (aquele da carga em movimento retilíneo e uniforme).

       Este fenômeno ocorre também com elétrons, desde que acelerados em direções específicas como, por exemplo, numa corrente elétrica ou entre as placas de um condensador ou, ainda, ao cair em direção ao núcleo de um átomo, quando da mudança de órbita.

       Como seria o campo de um elétron em um sistema de referencia não inercial? Como seria a equação do elétron nestas circunstâncias?

       A equação 6.3 é válida para um elétron em repouso no sistema de referência no qual vivemos. Esta equação não apresenta qualquer dependência temporal. Se o elétron estiver em repouso num referencial acelerado, sua equação deverá apresentar alguma dependência temporal; e a equação do elétron aprisionado em uma "órbita permitida" deve também assumir uma dependência temporal, neste caso periódica e com caráter estacionário.

       As equações apresentadas nos ítens anteriores foram deduzidas em um sistema de referência muito especial: aquele onde situava-se o laboratório de Coulomb ou, então, no sistema de referência no qual Newton deduziu as leis da mecânica. Como generalizá-las? O que é um referencial inercial?

       O sucesso da mecânica clássica é mais do que suficiente para nos garantir a existência de um referencial inercial. Apesar disso, a mecânica clássica ainda não obteve sucesso em definir um referencial inercial. Utilizando as palavras de Einstein e Infeld, a mecânica clássica flutua no ar, posto que não conhecemos regra alguma para determinar um sistema inercial [40].

       Em fins do século passado os físicos procuraram definir o sistema inercial não pela mecânica mas de forma a comportar a mecânica e a saída lógica foi a tentativa de conceituá-lo através de teorias de campo, das quais a mais profícua era a teoria de Maxwell. Assim sendo, pensou-se em caracterizar um referencial maxwelliano, o qual, no entanto, mostrou-se incompatível com os referenciais inerciais newtonianos [41]. Desta incompatibilidade, surgiu a física relativista de Einstein.

       Tendo em vista que estamos tentando interpretar o eletromagnetismo de um modo diferente daquele comumente adotado, é chegada a hora de desmistificarmos esta incompatibilidade. Direi então que:

7.2 Referenciais próprios e impróprios:

       A título de brevidade chamarei por referencial próprio aquele no qual o elétron em estudo mantém P e w constantes. Este é o referencial apropriado para a análise matemática do campo eletromagnético do elétron posto que o mesmo é função de w e r. Em particular, se o referencial próprio for um referencial inercial, o campo eletromagnético do elétron é função apenas destas duas variáveis vetoriais, conforme pode-se avaliar pelo estudo das equações 6.4 e 6.5. No restante deste artigo estudaremos somente campos produzidos por elétrons situados em referenciais inerciais próprios.

7.2.1 Observador situado no referencial próprio (inercial)

       Os campos x e b, quando observados através de referenciais impróprios, manifestam um efeito relacionado a um fenômeno descrito por Liénard (1898) e Wiechert (1900) para os potenciais da teoria de Maxwell. Este efeito deve ser analisado com extrema cautela posto que x e b são funções de duas variáveis (φ e w). Ambas contribuições são interessantes, porém  a devida a w assume extrema importância epistemológica, visto ser aquela que, ao não ser levada em conta, gerou consequências funestas para a física clássica [42]. A desconsideração desta parcela, a meu ver, colocou em evidência a pedra fundamental sobre a qual se apoiou a teoria da relatividade de Einstein.

       Vejamos, primeiramente, como φ se transforma. Com as considerações feitas no item 6.4, expressas pela equação 6.11, podemos admitir que sendo ρ um invariante, h, e consequentemente φ, transforma-se segundo o algoritmo

h = ρc        Û      h' = ρc' ,

com c' = c + v, em que v é a velocidade do elétron emissor de i.e.m. e observado do referencial impróprio considerado.

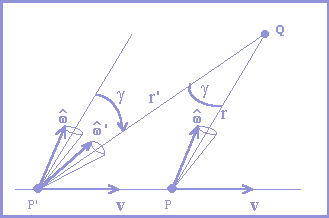
       Vejamos agora como w se transforma. Seja então um observador, situado em um ponto Q de um referencial inercial, e um elétron, situado em P e movendo-se, em relação a este referencial, com uma velocidade v constante. Direi, então, que o versor v manifesta-se ao observador em Q sob a forma de um outro versor v’, ou seja, v sofre uma aberração, conservando o seu módulo unitário. Para o cálculo desta aberração, observadas as convenções adotadas na figura 12, deve-se proceder da seguinte forma:

	Figura 12: Aberração de v (v Þ v'). P = posição do elétron num instante t em relação a um referencial inercial impróprio onde o elétron viaja a uma velocidade v constante emantendo v constante, e no qual o observador está em repouso em Q. P' = posição do elétron num instante retardado t' no qual o campo que chega a Q em t foi gerado.

1. Determinar o ponto P', admitindo-se que "o campo se propaga" radialmente a uma velocidade c, quando analisada do referencial próprio;
2. unir os pontos P, P' e Q;
3. traçar por P um tronco de cone com vértice em P e que contenha v em sua superfície, e com eixo na direção PQ;
4. transladar o cone juntamente com v para P';
5. rotacionar o cone em torno de P' e segundo um eixo perpendicular ao plano da figura (plano PP'Q) até que o eixo do cone se situe na direção P'Q;
6. o versor obtido por esta rotação de v é o versor v’.

       Como já afirmei em artigo anterior [40, op cit.], o escalar K, da hipótese 1 (e, portanto, o valor absoluto do vetor w), parece conter segredos relacionados aos referenciais inerciais, que somente a física experimental pode decifrar. Seria extremamente interessante verificar se o seu valor absoluto, uma vez definido, permanece ou não idêntico, qualquer que seja o referencial inercial considerado. A variabilidade de K seria um indício fortemente sugestivo a corroborar a intuição de Newton quanto à existência de um referencial absoluto. É de se esperar, no entanto, a observação de K aproximadamente constante para v << c.

7.3 O campo (x,b) do elétron em movimento:

       Conhecidas as transformações conformes para h e v, podemos desprezar os apóstrofos e assumir que os campos x e b de um elétron se expressam por

seja nos referenciais próprios, seja nos referenciais impróprios. Decorre então de 7.1 que, qualquer que seja o referencial inercial considerado, a soma x² + b² é uma função relativística clássica de posição:

h² = x² + b²

	Indice deste Artigo
Retornar		Avançar

DHTML Menu By Milonic JavaScript