3.1. Historical evolution:

In spite of the countless experiments produced by the current century, which can justify the presented hypotheses, it will be interesting to survey the historical evolution of electromagnetism on basis of its fundamental concepts. So we shall show the bases on which some paradigms are sustained, and the reader himself will judge whether he will keep on accepting them as absolute truths.

In 1729 Stephen Gray was the first to ascertain that electric virtue could transferred from a body to another one. Charles François Du Fay (1678-1739) showed that such virtue escaped from bodies without suitable isolation; and Pristley (1733-1804) noticed that electricity was distributed on the outer side of a metallic bottle, or in other, escaping from its interior [12]. From 1784 to 1789 Coulomb had his theory published: among his hypotheses there is one connected with this escape effect (the others will soon be introduced):

a) In an electrified conductive body the electric fluid spreads up to the surface but does not get into the body [13].

This fact was definitely confirmed by Faraday’s experiments and since then it has been corroborated with increasing precision. In the same way other properties were confirmed:

b) Bodies electrified by the same fluid repel one another; the bodies electrified by different fluids attract one another.
     c) The attractions or repulsings are produced in the direct reason of the densities or forces of the electric fluids, and in the inverse reason of the square of the distances [13].

Nowadays it is unreasonable to thing of electric fluid. Countless author, starting with Faraday in 1833, with the electrolysis law, ascertained through different methods the atomic nature of electricity. So we can state that too many electrons in a conductive medium go as far as the limits of their possibilities, that is, as far as the edges of the conductive medium and remain there. At first, in an almost instantaneous stage, we have a great amount of escaping electrons; after the balance is reached, we have an electric charge.

Coulomb’s law (hypothesis c above) is related to electric charges, with an implicit radial space polarization. If the electron, as seen in H-1, is a vectorial particle and if, as assumed in H-2, the space — in the absence of electrons — is isotropic, we might conclude from C-2 and C-3 that:

Up to 1800 the quantitative study of electric phenomena was practically restricted to the study of balance states, given the nearly instantaneous establishment of these states. With the invention of the voltaic cell new horizons were disclosed making the laws of stationary state easier to be achieved. In 1820 Hans Christian Oersted noticed that a compass suffered a deflection when placed next to a wire conducting a current [14], and this was possibly the greatest discovery in the history of electromagnetism. In less than a month, Biot and Savart measured the exercised force exerted by an electric current upon the pole of a magnetized needle [15] and from such mensurations Laplace deduced the Biot-Savart’s law for a current element traversed by an electric current i,

dF being the element of force acting on the north pole of a unitary magnet, and j the angle between r and ds vectors. Biot-Savart’s law — in its differential form (equation 3.1) — has some aspects which similar to Coulomb’s law, but reflecting the behavior of electrons in permanent escape, that is, elements of electric current with constant intensity i (stationary state). In its integral form it is knows as Ampere-Laplace’s law [16].

It is not easy to understand what an electric current element is. On the one hand it synthesizes electromagnetism under its simplest expression; on the other hand it does not exist except as a product of a brilliant human idea. It is something hypothetical e purely mathematical in its origins; it is a current that flows from nothing to nowhere and — when flowing through this real world — it is just a material point leaving us an equation which — if integrated into the infinite similar ids — produces a circuital law related to a real circuit. It is the subtlest and ingenious application of the differential calculation established from Newton’s age on.

Any similarity between an ids current element and an electron in movement is just coincidental for as time goes by the electron follows its course, while the abstract element remains in its position. Anyway, as we shall see it is possible to characterize the current element in a way which is not so abstract, and conclude:

Notice the contrast between C-1 and C-5.

Corollary 5 has no imposing character but can open a new path to us. This path, so long as we respect its inherent restrictions, can be quite useful.

Let us suppose a P point in space, arbitrary but fixed, and ids element — constant in s and in ds — in the circuit of an electric current. If we take Biot-Savart’s law (3.1) for granted we might state:

in which Y = senj/r² = constant. Therefore, if i is given, dF will be defined. Keeping in mind that

and substituting 3.3 in 3.2, we shall have

(3.4)

or

Two questions then arise: 1) What is the meaning of v and dq? 2) Is the second equality in 3.4 correct? Is this transformation allowed?

Quoting Spiegel [17], if dt is given, we can determine dq by means of 3.3, that is, dq is a dependent variable determined through the independent variable dt for a given t. This means that dq can assume any value we want, so long as we choose a convenient dt. So the aforementioned transformation will be allowed, so long as the differentials are tied or v = ds/dt may respect the dependence between dq e dt. Then it is convenient to choose a dq_e value for dq -- related to the number of electrons contained in ds and responsible for the dF field. Thus dq_e will be the electrolytic charge of the circuit measured in a dt’ time in which this charge crosses ds (it is a value of a theoretical nature and unsettled in itself). In this way it is easy to verify that v acquires the drag velocity characteristic v_a (v_a = ds/dt') of dq_e towards ds (v has the dimension of speed). Under these conditions, the expression 3.5 becomes

3.2. Microscopic theories:

The relationship cause(dq_e)-effect(dF) in the expression 3.6 — together with the operational indetermination of dq_e, increases theorization. So let us admit that the ids current element belongs to an ohmic conductive current i and that we can vary the current but keeping the ds element constant. The immediate consequences are given by 3.2: dF is proportional to i. If dF varies with i, then v_a and/or dq_e — according to equation 3.6 — should also vary. There are three theoretical possibilities:

a) dq_e is constant and dF depends exclusively on v_a;
b) v_a is constant and dF depends exclusively on dq_e;
c) dq_e and v_a vary with i.

We will discuss just the first possibility since it represents the basis of Drude’s (1900) and Lorentz’s (1909) theory concerning electric conduction, based on the free electrons model, or incompressible electric fluids model [18].

According to the incompressible electric fluids model in a conductor there exists a gas of electrons that does not by itself affect the intensity of the electromagnetic field for the negative charges are compensated by the positive ones. The mobile charges would be should be dragged by the electric field, and the speed of this movement v_a would be the only one to play some part in the genesis of the magnetic field. The dq_e factor in the expression 3.6. affect the modulation of dF exclusively in terms of the characterization of the structure of the conductive material. According to Tipler [19]:

This model successfully foretells Ohm’s law and it relates conductivity and resistance to the movement of the free electrons in a conductor. This classic theory is useful to the understanding of conduction, although it has been substituted for a more modern theory based on Quantum Mechanics.

In other words, the theory failed because it needed some ad hoc corrections that could make it compatible with the experimental discoveries; and whatever interpretation Quantum Mechanics might offer to the physical phenomenon, the truth is that the (a) possibility has not been experimentally confirmed.

So we leave this topic with a certainty which is backed by experiments: the magnetic field of a current element depends on the dq_e electrolytic charge contained in this element and consequently on the number of electrons that determine it. This fact — together with the cylindrical symmetry of the field — takes us to the following corollary:

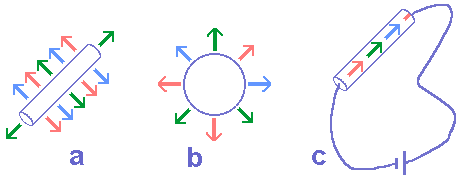
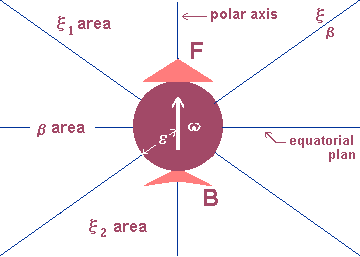
3.3 Electromagnetic properties of the electron:

Starting from hypotheses 1 to 4 and C-1 to C-6 corollaries, we may have a first idea of what an electric charge or an electric current is. Figure 2 is an image of this idea in which we may realize that the electric effects of an electron are related to its polar direction and the magnetic effects are related to the equatorial region.

Figure 2: a) Stationary electrons in a cylindrical conductor;
b) stationary electrons in a spherical conductor;
c) electrons in movement in a conductive wire.

The existence of two different kinds of electric charges (positive and negative), both associated to a different elementary particle (proton and electron respectively) and generating two different fields (centrifugal and centripetal respectively), allows us to conclude that the electrons (protons) posses two poles — F (for front) and B (for back) — and when they join the constitution of an electric charge they outwardly aim at only one of such poles — say, F. The reason for this direction preference will be understood later in this article.

Figure 3: Chiral symmetry electron-proton
(considered so only the electromagnetic properties).
The pole F is the pole that, in an electric charge, points outside.

The poles of similar protons and electrons in terms of direction are functionally opposed. In other words, the elementary particles of electromagnetism have a classic chiral symmetry (figure 3). Figure 4 supplies a first sketch of what we could call a physical electron, and in it we can also find the representation of a field of a mixed nature. Strictly speaking there is only one physical field: the A electromagnetic field (corollary 2); and this carried out three functions —and not just two— corresponding to three types of electromagnetic effect. It is possible to associate a secondary field to each of these effects: the x electric effect field, the b magnetic effect field and the t induction field or inductive effects. The term effect field associated to these secondary fields emphasizes the possibility of being noticed through test elements and —as a consequence— of mensuration. In the previous items we have already mentioned x and b fields, although in an incomplete way and with no intention of defining these fields. Now let us examine —in a very general way— what the t induction field is.

Figure 4: A first sketch of the physical electron
x₁ and x ₂: predominantly electric areas.
b: predominantly magnetic area.
ε: hypothetical electron radius.

A neutral body immersed in an A electromagnetic field occasionally plays the role of an electric or magnetic charge, depending of its structure and the field in question; this phenomenon is known since ancient times. The body is electrified or magnetized according to the characteristics of the original field. The induction reveals an accommodation of elementary particles, a phenomenon which is quite similar to what we described as escaping electrons in item 3.1. Here the particles move in obedience to the outer field; in it the electrons fled in obedience to the field other electrons provoked. This escape undoubtedly follows a given direction. How can a polar particle be directed? In order to it would be necessary more than a simple force field. Together with this field there should be necessary a torsion field! And this is the field that keeps the electrons in an electric charge or in an electric current, as shown in figure 2.

3.4 Critical points in the classical theories

In Maxwell’s theory there are countless conceptual blanks which gave birth to new theories; these theory although originally classic put classic electromagnetism at stake. Seemingly innocuous and conceived in a period of innumerable doubts concerning the inner structure of matter (between 1895 and 1915), they have a convergence point in common: all of them challenge experimentation. Countless times they showed incompatible with the classic logic but they only survived because they filled the above mentioned blanks. Acting together they prepared the favorable ground which was to support modern Physics. Here it is worth mentioning three of these theories, since they disagree with the electron image presented in the previous item: the theory of free electrons for conductors we have already mentioned; the theory of electric dipoles for dielectrics; and the theoretical idea that an accelerated electron always emits radiant energy, the great support of Bohr’s allowed orbits, that is, the areas where the electron is "authorized" to disrespect the imposed rule.

After Geiger and Marsden’s experiment (1909) concerning the scattering of alpha particles through a thin sheet of gold, Rutherford proposed a quite convincing [20]. nucleated atom model. Supported by Rutherford’s model and spectroscopic measurements related to the electromagnetic radiation emitted by atoms and deciphered from 1885 on, Bohr (1913) developed the "On the constitution of atoms and molecules" theory [21]. The hypotheses proposed by Bohr were later synthesized in four basic postulates; two of them, extracted from Eisberg and Resnick [20], reads:

BP3 is more questionable, although less disputable than BP1, since it translates into words what is observed in the laboratory. We cannot state the same thing concerning BP1: no experiments have been reported demonstrating in an unrefutable way that the interactions electron-nucleus are mediated by Coulomb’s forces. On the contrary, most experiments undertaken in the 20th century confirm a single truth: electrons ignore Coulomb’s law.

In 1911 Kamerlingh Onnes discovered a quite interesting phenomenon: the superconductivity of mercury. In a superconductor, as it was later observed, there circulate electric currents that go on doing so for several years without decreasing at all. Therefor, in a superconductor electrons travel in trajectories in which they "are allowed" to disrespect the classic electromagnetic theory. Up to 1957, there was practically no explanation for this phenomenon. The greatest difficulty for theorization was the incompatibility between the superconductivity and Drude and Lorentz’s electric conduction theory mentioned above. In 1957 Bardeen, Cooper and Schrieffer (BCS) decided to ignore the theory concerning free electrons, and proposed a model which was compatible with experimental results. The BCS theory met with a great acceptance, and — due to its success — the following truths were then taken for granted: BP3 is true, the BCS theory is true, Maxwell’s equations are true, and the theory concerning free electrons is true. So many incompatible truths eventually made scientific methodology to be rejected. And something proved false: Popper’s logic [22].

The disagreement about the theme is not restricted to Physics. In Chemistry the hybrid of resonance are a good example, such as the benzene structure. In it, six electrons circulate — regardless of all theoretical predictions — just like the electrons of an excited superconductor, giving benzene an extra stability which is hard to be explained [23]. The oxidation-reduction reactions are also problematic: they present themselves in two thermodynamic versions and it seems that all previsions in accordance to Maxwell’s theory — as in the case of conductors — do work well exclusively in the irreversible version. In this obscure section of Chemistry we also have the "intersection of states model" (ISM) developed by Formosinho and Varandas [24]; This model seems to suggest — in the case of the oxidation-reduction reactions — the existent of an intermediate state in which the electrons would transit according to ephemeral and allowed macro-orbits, i.e., without irradiating energy.

In biophysics there are two metabolic processes of vital importance: the cellular respiration and photosynthesis. Chains transporting electrons, indifferent to the classic Physics postulates, are coupled to systems storing the energy that should be irradiated in it by the decelerated electrons. This phenomenon was presented by Szent Györgyi, when he was in New Jersey (Princeton, USA), as follows:

What is notable in this case is that the electrons exactly know what they should do. Thus, this small electron knows something that all the wise people in Princeton ignore, something that only be a very simple thing [25].

The energy stored during this deceleration is turned into chemical energy through oxidative phosphorylation. According to Peter Dennins Mitchell this is processed thanks to the mediation of a polarized enzymatic system located in the inner membrane of the mitochondrion allowing the transport of protons through the membrane, in obedience to a protomotive gradient [26]; and the protons there accelerated leave their non-irradiated energy with the ATP. Therefore, it exists an enzymatic trajectory where the protons, in a similar way to Bohr’s electrons, are authorized to disrespect the classic rule. In all the above-mentioned examples the allowed trajectories are areas of adiabatic confinement, i.e. the processes that use them present a reversible character.

The atom conception as a planetary system, based on Rutherford’s model, although it became the only plausible hypothesis, also puzzled the physicists of his time. The solution of the dilemma was found by Bohr through other postulates (BP2 and BP4 according to Eisberg’s numeration). These postulates are strategic in the sense that they are in agreement with experimentation; at the same time they disguise the absurd coexistence among the other postulates (BP1 and BP3). In fact, in BP2 Bohr refers to the infinite possible orbits, according to classic mechanics. Classic mechanics only starts acting when the forces of interaction electron-proton are defined; and as we have seen, if these interactions are Coulomb forces, BP3 is false, or vice-versa. So up till now classic mechanics cannot give any guarantee concerning the possible number of orbits.

Whatever the proton-electron or nucleus-electrons relationship might be, the truth is that the resulting grouping should be much more complex than a pair of binary stars, or a planetary system kept in a stationary state by inertia and gravitational interactions.

Now let us see something about the theory of electric dipoles. We know that conductors, when submitted to an electromotive force, become headquarters of an electric current; but if the conductor has been isolated from the field source —as in Figure 5a— the current will soon cease, and this will happen when a certain threshold is established for the separation of charges in the conductor. In his studies on capacitors, Faraday noticed that dielectrics, although they do not conduct electric currents, manifest a qualitatively similar behavior. These materials resist in part to the penetration of the electric field in its interior, a phenomenon that in some aspects reminds Archimedes’s buoyant force, as opposed to the gravitational field.

Figure 5: Comments in the text

By the end of the era of electric fluids, there appeared a promising theory in order to explain this phenomenon (electric polarization of dielectrics). This theory admitted the dielectric constituted by small conductive spheres immersed in an insulating environment [27]; the complex phenomenon was reduced to a summational of simple effects, as shown in Figure 5b. The theory is perfect within the proposed limits although, in spite of its representativeness —and to use Mario Bunge’s words [28]— it can be considered of low risk since it explains what is observed (phenomenological or behaviorist character) through an internal mechanism (representative character) of secondary importance. In other words, the microscopic model (Figure 5b) does not modify at all the model from which it originated (Figure 5a).

In the beginning of the atomic era the situation was no longer the same —the conductive spheres were identified with Thomson’s atoms and the insulating environment to the ether between them. The representative character of the theory increased in importance and transformed it into a high risk theory.

After the identification of the corpuscular character of the cathodic rays (1897) —such corpuscles were later called electrons— Thomson suggested that the positive charge of an atom could be uniformly distributed in a sphere with negative corpuscles inside the positive charge [27]. On the other hand, as Tipler says [29], Thomson saw the atom as a positively load fluid, with the electrons plunged in a stable configuration in order to make the group neuter. Due to mutual repulse, as described by Eisberg et al. [op. cit. in 20], the electrons would be uniformly distributed in the positive load sphere whence the so called plum pudding model; and when the vibrates the electrons would vibrate around their equilibrium positions which would explain —in terms of quality— the emission of electromagnetic radiation.

The free electrons theory was soon after developed (1900-1909) and it is not hard to recover its logic: if the positive fluids of Thomson’s atoms intercommunicate somehow or constitute a single amorphous mass whose electrons are practically free although attached to the mass as a whole. If such thing happens, the material is a conductor; otherwise it is a dielectric. Although the idea of negative particles still existed, the idea of fluid persisted, and physicists of the time were about to imagine the models presented in Figures 5a and 5b as electric dipoles, since they were very similar to the macroscopic group represented by both Coulomb’s charges with the same intensity and opposite signs.

The notion of static electric dipole also appeared and germinated an akin concept: the dynamic electric dipole. Hertz’s experiments and Thomson’s model favored this conception. In fact, the radio transmitter and radio receiver used by Hertz are called dipole antennae; and the plum pudding model —with electrons vibrating around an equilibrium position— reminds these antennae. With this model in mind, in his theory of thermal radiation emission Planck states that the emitting surface contains electrons which are tied to fixed points through forces obeying Hooke’s law [30].

While Thomson’s model was still accepted, the free electrons theory represented a branch of this tree and the idea of microscopic dipoles stemmed from another of its branches. Nevertheless there were too many experimental restrictions to the model, and Thomson —in spite of his elaborated mathematical calculations— was unable to achieve general agreement concerning experimentation [op. cit in 29]. Due to Rutherford’s conclusive analysis of the atom nucleus, the tree was cut down, but its branches had already blossomed. Electric polarization in dielectris and radiation emission were again explained by phenomenological theories; although of low risk such theories were endowed with a very intensive abstractionism. The atomic dipoles kept few physical characteristics, but a lot of mathematical ones.

An atom of hydrogen (Rutheford’s model) possesses a dipole momentum vectors that varies according to time, and according to Goldenberg, it should generate a variable electric field in time and, therefore, should emit electromagnetic radiation. Although classically correct, this conclusion presupposes the non-existence of stationary electric fields, a supposition which is not backed by experimentation.

The absence of this radiation in the normal atom of hydrogen was one of the great paradoxes found in the primitive quantum physics [31], and it was solved only through the acceptance of an undulatory electron: the electronic structure of atoms and molecules can be represented by a single cloud of negative charges [31], an image that reminds an inverse Thomson model: a (fluid) cloud negatively loaded with a punctiform and positive nucleus located inside the negative charge. In other words, the electric dipole —as it is conceived today— is incompatible with classic electromagnetism; the principles of classic electromagnetism are imperfect to explain the paradox it generated.

	Contents
Return		Advance