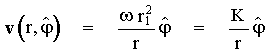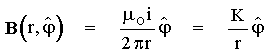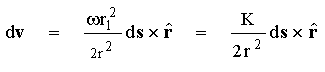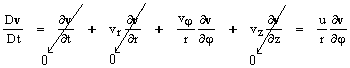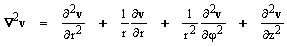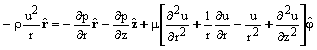Similaridades entre Campos de Velocidade e o Campo Eletromagnético

Alberto Mesquita Filho
Integração I(1):15-9,1995

Introdução

Cilindros Girantes

Plataformas Girantes

Discussão

Apêndices

I — Introdução

O rotor de Flettner, princípio ativo do barco de Flettner, foi provavelmente a primeira aplicação prática de um efeito descrito por Magnus em 1850. Este efeito explicava desvios laterais importantes sofridos por balas de canhão. Posteriormente, Lord Rayleigh constatou o mesmo fenômeno em bolas de tênis.

A idealização do rotor de Flettner apoia-se totalmente nas experiências de Prandtl, e sua lógica em leis descobertas duzentos anos antes por Euler e Bernoulli. O barco de Flettner é dotado de cilindros verticais mantidos em rotação por pequenos motores. Sua força motriz depende exclusivamente do vento, e a seção transversal, oposta ao vento, é cerca de dez vezes menor do que a aparelhagem de um barco a vela de mesma potência [1]. O curioso, e o que pasma o leigo, é a direção da força em relação à direção do vento (figura 1).

Figura 1 - O barco de Flettner

E o que diria um físico se questionado a respeito? Shames (1962), ao fazer uma abordagem introdutória no estudo de campos de velocidade, classifica as forças em dois tipos: forças de campo e forças de contato. Visto sob este prisma, um campo de velocidades não se constitui num campo de forças, conquanto esteja associado a forças. E com efeito, via de regra não é possível caracterizar, num campo de velocidades, uma propriedade física relacionada apenas às forças de contato e dada por uma função da posição e do tempo, o que seria de se esperar se tal região fosse sede de um campo de forças, como definido por Alonso et al.(1970). Por outro lado, campo de forças implica numa ação à distância, o que à primeira vista se opõe à idéia de força de contato.

Visto sob um prisma puramente matemático, não há distinção entre campo de forças e campo de velocidades. Suas equações são, em geral, similares. Este fato é bem explorado por Feynman et al. (1972) em quase toda sua obra: equações iguais têm soluções iguais. E, com efeito, não são raras as situações em que equações hidrodinâmicas se confundem com as equações de Maxwell.

Se, por um lado, campo de velocidades não é um campo de forças; o efeito Magnus, por outro, parece nos afirmar o contrário. Questionemo-nos: Qual seria o campo de velocidades de um cilindro, girando verticalmente num meio viscoso newtoniano? E qual seria o efeito deste campo sobre um pequeno objeto de prova girante, digamos um pião, colocado neste campo sobre uma superfície lisa? A figura 2, apoiada em nossos conhecimentos de simetria, viscosidade e efeito observado ao analisarmos o exposto na figura 1, responde qualitativamente a estas perguntas.

Este campo de forças não difere conceitualmente de um campo gravitacional ou elétrico. No caso gravitacional, corpos dotados de massa se atraem; no caso elétrico, corpos dotados de carga se atraem ou se repelem; aqui, corpos dotados de giro se atraem ou se repelem, conforme o giro seja no mesmo sentido ou em sentidos opostos. E conquanto a força, encarada sob um prisma hidrodinâmico, seja uma força local, trata-se, sem sombra de dúvidas, de uma ação à distância. Que dizer de uma análise quantitativa?

II — Cilindros Girantes

O campo de velocidades de um cilindro girante de extensão infinita, imerso num fluido newtoniano, é dado pela equação de Navier-Stokes com as condições de contorno impostas. Sua solução estacionária para fluidos incompressíveis e de viscosidade constante (equação simplificada) está demonstrada no Apêndice B. Pode-se obtê-la também de dados da literatura como um caso particular da solução para o viscosímetro de Couette, ou seja, com o raio do cilindro exterior do mesmo tendendo a infinito. Obtém-se então:

(1)

sendo K constante, ω a velocidade angular do cilindro, r₁ seu raio e r a distância do ponto considerado ao eixo do cilindro (corresponde ao ρ do sistema de coordenadas cilíndricas). O campo é idêntico do ponto de vista geométrico, bem como analítico, ao campo magnético B produzido por um fio de corrente retilínea de extensão infinita:

(2)

A expressão (2), obtida pela primeira vez por Biot e Savart em 1820, foi desintegrada por Laplace que chegou à expressão do campo produzido por um elemento de corrente ids (Locqueneux, 1989), expressão esta conhecida como lei de Biot-Savart, ou ainda, lei de Ampère-Laplace, e expressa atualmente por

(3)

Adotando-se a postura de Feynman, citada na introdução, podemos então escrever:

(4)

em que dv(r) seria o campo de velocidades de um elemento de cilindro (Notar que r, agora, representa uma medida em coordenadas esféricas). Mas o que seria tal elemento de cilindro? Obviamente, trata-se de uma entidade matemática, e não física, tal e qual o elemento ids da lei de Biot-Savart. É importante perceber que dv(r), dado por (4), não é o campo de um cilindro infinitesimal de raio r₁, posto que a equação não leva em conta os efeitos de suas superfícies não laterais. E, com efeito, estas superfícies não contribuem para a expressão original (1). Tampouco é o campo de um anel, posto que não há também nenhuma contribuição da superfície interna. dv(r) é portanto uma idealização matemática do mesmo tipo que dB(r) dado por (3).

Se em eletromagnetismo é extremamente difícil, se não impossível, evoluir de um elemento ideal para o real (que no caso seria um elétron ou um conjunto de elétrons em movimento), em mecânica dos fluidos tal não se dá. É perfeitamente possível estimar-se os efeitos de um elemento real de cilindro de altura ds que gere um campo em consonância com a equação de Navier-Stokes. A tarefa pode não ser fácil, mas é possível. E não é fácil posto que a equação citada é não-linear, ou seja, o princípio da superposição, como regra, não é obedecido. De qualquer forma, vamos verificar no item a seguir o campo de um disco de raio r₁ em rotação, qual seja, o campo produzido isoladamente pela superfície circular de um elemento de cilindro real.

III — Plataformas Girantes

A solução estacionária da equação de Navier-Stokes simplificada, e para uma plataforma girante de dimensões infinitas (giro em torno de um eixo na origem), conforme demonstrado no apêndice C, é dada pela seguinte expressão:

v(r) = wr = w´ r

(5)

Nestas condições temos um campo de vorticidades constante, pois

Ñ´v = w = constante

(6)

Chama a atenção a semelhança geométrica e analítica entre o campo de vorticidades de uma plataforma infinita e o campo elétrico de uma superfície plana infinita e carregada uniformemente. É de se notar que em nenhum momento, na obtenção de (5), pesou significativamente o fato de o raio da plataforma tender a infinito. Resultado análogo seria obtido restringindo-se o domínio da função v(r) a 0 £ r £ R. A solução, com este domínio, é:

v(r) = w´r = (Ñ´v)´r,

[0 £ r £ R]

(7)

A solução (7) é uma solução estacionária e, portanto, obtida num tempo infinito. Nestas condições, e fora do domínio considerado, o campo de um disco de raio R seria idêntico ao produzido por um cilindro infinito de raio R e mesma velocidade angular. Em outras palavras, vê-se por (7) que o fluido gira em 0 £ r £ R como um corpo rígido de diâmetro 2R, ou seja, neste domínio o fluido comporta-se tal e qual um cilindro sólido.

Fisicamente podemos pensar no disco como que transferindo energia e momento angular ao fluido contido no domínio considerado; e este fluido em rotação, por sua vez, como que transferindo energia e momento linear ao fluido fora do mesmo. Esta solução é a única, para a condição idealizada [6], que compatibiliza as leis de conservação de energia, momento linear e momento angular. Estas leis, de uma forma até certo ponto fantástica, estão contidas na expressão matemática da equação de Navier-Stokes. A solução concorda também com os teoremas de Helmholtz que traduzem a lei de conservação de momento linear aplicada a um fluido (Feynman et al, op. cit) e que nos afirmam que, tal e qual as linhas de um campo elétrico, as linhas de campo de vorticidades jamais começam ou terminam num espaço sem agentes causais.

IV — Discussão

Conforme visto, as similaridades entre campos de velocidade e eletromagnético ultrapassam os limites do que poderíamos chamar uma coincidência fantástica. Não por outro motivo Maxwell, durante grande parte de sua vida, tentou explicar os fenômenos eletromagnéticos através de analogias hidrodinâmicas. Há que se destacar três empecilhos a dificultar os que se propuserem a persistir neste caminho:

Como explicar, através de um modelo hidrodinâmico, a existência de dois tipos de cargas elétricas? Em que momento ou fase da construção do modelo ocorre a quebra de simetria, e como seria esta quebra?

Como equacionar o eletromagnetismo através de um modelo hidrodinâmico sem apelar para a existência de um éter que desde os tempos newtonianos tem-se mostrado como um meio inútil, teoricamente nefasto e muito provavelmente inexistente?

Como partir de um modelo que se apóia em uma única equação de campo e evoluir para a explicação de uma teoria que se apoia em quatro equações irredutíveis?

Como se vê, a tarefa não é fácil. Mas quem nos garante que a teoria de Maxwell está completa? Não estaríamos tentando percorrer um caminho inverso ao da razão? Ao contrário do que se afirma, as equações de Maxwell nem sempre são válidas: os precursores da mecânica quântica que o digam. A equação de Navier-Stokes, por sua vez, tem-se mostrado até o momento, absoluta. Seria mais lógico então que procurássemos por um modelo eletromagnético que explicasse fenômenos hidrodinâmicos, posto que a hidrodinâmica apóia-se em agentes macroscópicos e o eletromagnetismo, ao contrário, foi concebido com a finalidade de explicar efeitos provocados por agentes do microcosmo interpretados, na época, como flúidos mas hoje sabidamente representados por partículas elementares. Este modelo, caso exista, certamente se mostrará incompatível com a teoria de Maxwell, pois, caso contrário, nem teoria da relatividade nem mecânica quântica justificariam sua razão de existir.

Este é um tema em aberto e que merece um destaque maior por parte da coletividade científica. Para que possamos, quem sabe, um dia, considerar o lamento de Einstein (op. cit.), expresso a seguir, uma curiosidade histórico-acadêmica:

A história das descobertas científicas e técnicas revela-nos quanto o espírito humano carece de idéias originais e de imaginação criadora. E mesmo quando as condições exteriores e científicas para o aparecimento de uma idéia já existem há muito, será preciso, na maioria dos casos, uma outra causa exterior a fim de que se chegue a se concretizar. O homem tem, no sentido literal da palavra, que se chocar contra o fato para que a solução lhe apareça. Verdade bem comum e pouco exaltante para nosso orgulho, e que se verifica perfeitamente no barco de Flettner. E atualmente este exemplo continua espantando todo mundo!

* * * * *

V — Apêndices

Apêndice A ¾ Obtenção das equações derivadas da equação de Navier-Stokes para condição estacionária e com simetria cilíndrica.

A equação de Navier-Stokes, simplificada para um fluido incompressível e com viscosidade μ constante, é dada por [7]:

(1)

B representa as forças externas, sendo em geral dado por -ρÑy (y = potencial gravitacional), ρ a massa específica do fluido e p a pressão.

Observando-se que

Þ Condição estacionária

e

v(r,φ ,z) = (0, v_φ , 0) = (0, u, 0)

Þ

Condição de Simetria

com u = v_φ e u = u(r,z),obtemos as simplificações abaixo:

a)

Como

obtemos:

(2)

b)

(3)

c)

B = 0

(4)

(efeitos gravitacionais desprezíveis - situação ideal)

d)

Portanto:

(5)

Substituindo (2), (3), (4) e (5) em (1), temos:

(6)

De (6) obtemos as seguintes equações estacionárias, validas para campos com simetria cilíndrica do tipo u = u(r,z):

(7)

(8)

(9)

Apêndice B ¾ Solução da equação 9 (obtida no Apêndice A) para um cilindro girante de raio r₁ e altura infinita.

(solução idealizada posto que desprezamos efeitos gravitacionais)

Neste caso temos e a equação (9) do Apêndice A fica:

(1)

As condições de contorno adicionais são:

u(r₁) = wr₁

(2)

u(¥) = 0

(3)

Deve-se observar que, de (1), u = u(r), e visto que

a equação (1) é equivalente a

Efetuando-se a mudança de variável y = u/r, chegamos a:

.

E, então, com , temos:

Então, segue-se a sequência de transformações:

(4)

De (3) e (4) conclui-se que C = 0 e, portanto:

(5)

De (2) e (5) obtemos:

,

Portanto:

Para dois cilindros concêntricos de raios r₁ e r₂, o raciocínio é semelhante. Chega-se a (4) e, com as novas condições de contorno [u(r₁) = w₁r₁ e u(r₂) = w₂r₂], determinam-se as constantes k e C (duas equações a duas incógnitas).

Apêndice C ¾ Solução da equação 9 (obtida no Apêndice A) para uma plataforma girante de raio R com R ® ¥, e altura h.

As condições de contorno adicionais são:

u(r,0) = wr

(1)

0 £ u(r,z) £ wr

(2)

Tentemos a seguinte separação de variáveis:

u(r,z) = R(r)Z(z).

As soluções parciais assim obtidas são de difícil análise e agrupamento. A solução em Z(z) é uma exponencial, e a solução em R(r) uma função de Bessel J₁(lr) associada a uma função de Newmann N₁(lr). É de se notar que l, tanto na exponencial quanto em R(r) tende a zero, levando-nos a condições de singularidade notáveis. Com efeito, a condição de contorno (1) é muito rígida mas, por outro lado, percebe-se que é exatamente este fato que torna a solução do problema direta, pois:

u(r,0) = R(r)Z(0) = wr

(3)

e

Z(0) = A = constante

(4)

Analisemos A sob dois aspectos:

Caso 1: A = 0.

Se A = 0, de (3) e (4) obtemos R(r) ® ¥ e, de (2), Z(z) = 0, " z. Nestas condições u = u(r) e a condição de contorno (1) é a solução:

u(r) = wr

(5)

Caso 2: A ¹ 0.

Temos então de (3) e (4): R(r) . Nestas condições:

(6)

e

ý

(7)

Substituindo (6) e (7) em (9-A):

ou

Portanto, Z(z) = Bz + C. Então, de (6):

De (1)

Portanto,

u(r,z) = wr(1 - kz)

(8)

com .

De (2), u(r,z) £ wr, "z Þ k ³ 0. E como, também de (2):

0 £ wr(1 - kz) £ wr e wr > 0,

temos:

0 £ 1 - kz £ 1, ou
1 ³ kz ³ 0, "z.

Portanto:

k = 0,

e de (8):

u(r,z) = u(r) = wr,

expressão esta idêntica à obtida em (5) para A = 0. Consequentemente,

u(r) = wr

Referências:
[1] - EINSTEIN, A., Como Vejo o Mundo, Ed. Nova Fronteira, 1981, São Paulo.
[2] - SHAMES, I.H., Mecânica dos Fluidos, vol. 1, Princípios Básicos, Ed. Edgard Blücher Ltda, 1973, São Paulo.
[3] - ALONSO, M., FINN, E.J., Física, vol.1, Mecanica, Fondo Educ. Interamer. S.A., Madrid, 1970.
[4] - FEYNMAN, R., LEIGHTON, R.B., Física, vol II, electromagnetismo y materia, Addison-Wesley Iberoamer., Mexico, 1972.
[5] - LOCQUENEUX, R., História da Física, Publ. Europa-América, Portugual, 1989.
[6] - Por condição idealizada queremos nos referir a fluido newtoniano incompressível, e estabilizado em termos de velocidade após um tempo infinito.
[7] - HUGHES, W.F., BRIGHTON, J.A., Fluid Dynamics, Mc. Graw-Hill Inc. (Shaum's Outline Series), New York, 1991, p. 54.

Outras obras consultadas e não citadas no texto:
· CATTANI, M.S.D., Elementos de Mecânica dos Fluidos, Ed. Edgard Blücher Ltda, São Paulo, 1990.
· EISBERG, R.M., LERNER, L.S., Física, vol. 3, Fundamentos e Aplicações, Ediciones URMO, Bilbao (Espanha), 1973
· MESQUITA F.°, A., A Equação do Elétron e o Eletromagnetismo, Editora Ateniense, São Paulo, 1993.
· PAY, SHIH-I, Viscous Flow Theory, I - Laminar Flow (p. 54 e 55), consultado na biblioteca do IFUSP (não possuo mais dados).
· PINSKY, M.A., Partial Differential Equations and Boundary-Value Problems with Applications, Mc.Graw-Hill Inc., New York, 1991