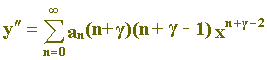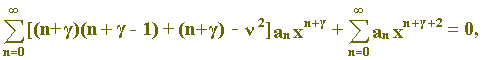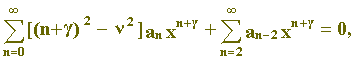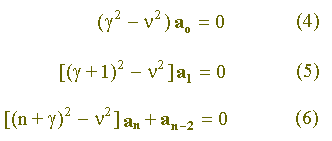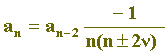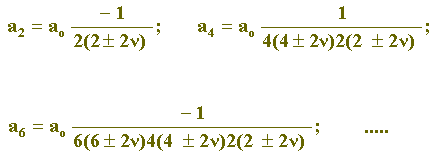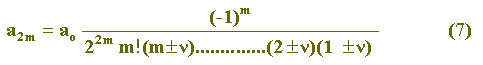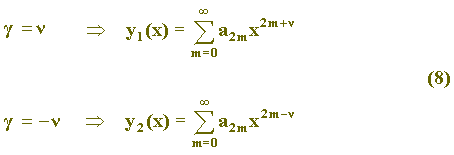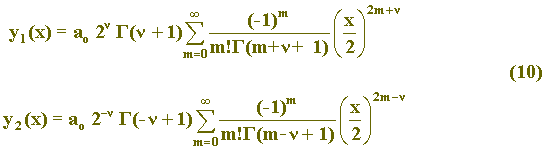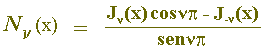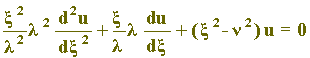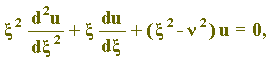A Equação de Bessel

Alberto Mesquita Filho
Integração II(5):101-6,1996

1ª. Parte

Sumário: O propósito deste artigo é resumir os tópicos essenciais relacionados a uma equação que surge com grande frequência, em engenharia e/ou física matemática, quando da resolução de equações diferenciais parciais pelo método da separação de variáveis. Embora escrito em forma didática, o artigo é dirigido a estudantes interessados no tema, e que estejam familiarizados com o cálculo avançado. Presta-se também a fornecer subsídios ao leitor que pretenda recordar rapidamente este interessante capítulo da física matemática, bem como a auxiliá-lo na caracterização e/ou memorização de alguns dos "macetes" indispensáveis para a resolução de problemas afins: fórmulas (ou relações) de recorrência, função geratriz e ortogonalidade.

1 Conceituação e ocorrência

A equação

é a chamada equação diferencial de Bessel de ordem . A restrição x > 0 é essencial, pois não existe solução GERAL para intervalos que contenham x = 0 [1]. Em alguns textos, a equação de Bessel surge sob uma forma mais completa [2],

na qual os parâmetros constantes recebem a seguinte denominação:

d dimensão;
l autovalor;
μ = ² índice angular;
ordem da equação de Bessel.

Se d = 2 e l = ±1, a equação (2) transforma-se na (1).

É comum o aparecimento da equação (2) quando da resolução de equações diferenciais parciais da física pelo método de separação de variáveis. Nestes casos, quando o problema é resolvido em coordenadas cilíndricas obtém-se d = 2, e, quando em coordenadas esféricas, d = 3. Em coordenadas cilíndricas, havendo simetria circular, obtém-se = 0; caso contrário, para soluções não simétricas, = 1, 2, 3, ...

No número 1 de Integração [3] fez-se referência ao surgimento da equação de Bessel quando da resolução de um caso particular da equação de Navier-Stokes. Na ocasião, graças às condições de contorno um tanto rígidas, pudemos chegar à solução sem nos utilizarmos das técnicas que serão aqui apresentadas.

É interessante notar que tanto a equação (1) quanto a (2) pertencem ao tipo de equações estudadas na teoria de Sturm-Liouville, podendo ser escritas na forma:

[s(x)y']' + [lr(x) - q(x)]y = 0

onde r(x) é a chamada função peso. Sob esta forma, a equação (1) fica:

com s(x) = r(x) = x, q(x) = ²/x e l = 1.

2. Solução da Equação (1) em série de potências

Seja uma possível solução de (1). Ao admitirmos esta possibilidade, na realidade o que estamos fazendo é assumir y, dado pela equação acima, como solução de (1), e propondo-nos a determinar os coeficientes an, bem como g. Nestas condições temos

e

Substituindo estes valores de y, y’ e y" em (1) obtemos:

ou

ou ainda,

A equação (3) pode ser desmembrada em três igualdades:

As igualdades (4) e (6) são chamadas, respectivamente, equação indicial e equação de recorrência.

Da equação indicial, e assumindo a_o ¹ 0, vem

g = ±

o que implica, de (5), em:

a₁ = 0.

A equação de recorrência (6) pode ser escrita na forma:

e como a₁ = 0, segue-se que todos os coeficientes a_n com índice ímpar são nulos: a₃ = a₅ = a₇ = ... = 0. Por outro lado, os coeficientes a_n com índice par são dados por:

Generalizando, temos:

Efetuando a mudança de variável n Þ m tal que n = 2m, os coeficientes a_n podem ser expressos por:

ou

ou, finalmente:

Lembrando que , n = 2m e g = ± , temos:

Substituindo (7) em (8) as soluções y₁(x) e y₂(x) ficam:

As expressões (9) podem ainda ser escritas, em termos de funções gama () [4], da seguinte maneira:

Determinadas duas soluções y₁ e y₂ para a equação (1), podemos, uma vez comprovada a existência destas soluções, bem como sua independência linear, escrever a solução geral como

y(x) = C₁y₁(x) + C₂y₂(x).                  (11)

No item a seguir veremos que (11), com y₁ e y₂ dados por (10), não é solução geral válida para = 0, 1, 2, ...

3. Funções de Bessel

A função de Bessel de primeira espécie e ordem é definida por:

                  (12)

Segue-se, então, de (10), (11) e (12):

y(x) = C₁a_o2 ( +1)J(x) + C₂a_o2^- (- +1)J_-(x);

ou, agrupando-se as constantes:

y(x) = AJ(x) + BJ-(x),      ¹ 0,1,2,...               (13)

Se = 0, temos ( +1) = +1) = (1) e, nestas condições, J(x) = J_-(x) = J_o(x). Consequentemente, y₁(x) = y₂(x) e, portanto, y(x), dado por (13), não é solução geral.

Por outro lado, se k Z⁺, temos

Nestas condições, y₂(x), dado por (11), não existe, e, portanto, não é solução de (1). É interessante notar que, neste caso, J_-(x) existe, sendo possível demonstrar que:

Z⁺ Þ J(x) = (-1)J_-(x)

ou seja, J(x) e J_-(x) são linearmente dependentes.

Demonstra-se [5] também que, para inteiro, a solução geral de (1) é dada por

y(x) = AJ(x) + BN(x)                       (14)

com

N(x) é chamado função de Bessel de segunda espécie [6], de ordem , ou função de Newmann [7].

4 Solução da equação de Bessel para l¹1

Seja a equação

               (15)

Mudando a variável x para x = lx, temos

Portanto:

ou

cuja solução, tendo em vista (1) e (14), é:

u(x) = AJ(x) + BN(x).

Então, a solução de (15) é

u(x,l) = AJ(lx) + BN(lx).

 

Para ir para o próximo capítulo clique na figura ao lado Þ

A seguir:

5. Fórmulas de recorrência das funções de Bessel
6. Função geratriz
7. Ortogonalidade das Funções de Bessel

Referências:

1. A equação x2y’’ + xy’ - y = 0 representa um caso mais simples (não é equação de Bessel) onde também se verifica tal restrição (x > 0). Sua solução geral, conforme pode ser facilmente verificado, é y = C1x + C2/x. Esta solução não está definida para x = 0.
2. Vide, por exemplo, PINSKY, M. A., (1991), Partial Differential Equations and Boundary-Value Problems with Applications, Mc. Graw-Hill Inc., New York, p. 174.
3. MESQUITA F.° , A., Similaridades entre campos de velocidade e o campo eletromagnético, Integração I(1):15-19, 1995, apêndice C (p. 18).
4. A função gama goza da seguinte propriedade: (z+1) = z(z). Portanto: (m+p+1) = (m+p)(m+p) = (m+p)(m-1+p)(m-1+p) = (m+p)(m-1+p)(m-2+p)(m-2+p) = (m+p)(m-1+p).........(1+p)(1+p). Então, (m+p)(m-1+p)......(1+p) = . Analogamente, mostra-se que (m-p)(m-1-p).......(1-p) = .
5. A demonstração está além do escopo deste artigo.
6. Existem outras funções de Bessel, não havendo concordância quanto à notação adotada para a função de segunda espécie.
7. Observação: Se for metade de um inteiro ímpar, J(x) pode ser expresso em termos de senos e cossenos.

DHTML Menu By Milonic JavaScript