Introdução à físico-química das soluções

Alberto Mesquita Filho

Página 4

C. SOLUÇÕES LÍQUIDAS (continuação)

C-5 SOLUÇÃO DE GÁS EM LÍQUIDO

Consideremos um sistema de volume constante ao qual, após ter sido criado vácuo, adicionou-se um líquido volátil 1 em quantidade Φ₁ suficiente para que se constituíssem duas fases: líquido e vapor (figura 25). Nestas condições, a pressão será a pressão de vapor da substância pura 1 na temperatura da experiência.

Mantendo-se a temperatura constante, adicionemos progressivamente Φ_2i moles de um gás 2 ao sistema e estudemo-lo em i condições (i = 1, 2, 3, ...).

À medida em que o número de moléculas do gás 2 aumenta, sua pressão parcial, medida por um manômetro seletivo M_s, também aumentará. Nestas condições, cada vez maior será a probabilidade de uma molécula de 2 se chocar com a fase líquida e/ou penetrar na mesma. Portanto, uma fração do gás 2 diluir-se-á no líquido 1.

O fenômeno inverso também começa a se processar: o escape das moléculas de gás 2 da fase líquida. Numa situação i de equilíbrio, o número de moléculas de 2 que se diluem no líquido 1 na unidade de tempo é igual ao número de moléculas de 2 que escapam da fase líquida. E a concentração do gás no líquido dependerá apenas da pressão parcial do mesmo, para uma temperatura constante.

Para as moléculas que se diluem, o significado físico do processo é bastante semelhante ao da condensação, pois embora não exista o agrupamento espontâneo, assim que elas penetram no sistema condensado (fase líquida), ficam sujeitas a forças de coesão bastante intensas. E a tendência ao escape iguala a tendência à permanência na fase líquida.

A pressão parcial do gás 2 representa uma medida da tendência ao escape das moléculas de 2 da fase líquida para a fase gasosa. Para gases com a temperatura abaixo da temperatura crítica, esta nada mais é senão a pressão de vapor da substância considerada na fase líquida. Quando T > T_c, esta pressão é chamada simplesmente pressão parcial do gás na fase líquida.

[É importante que se perceba que estamos aqui expandindo o conceito até agora apresentado como pressão de vapor. Como veremos abaixo, a pressão de vapor na fase líquida, enquanto mistura, não é a mesma pressão de vapor da substância pura, se bem que possamos pensar nesta última como um limite da primeira, para a mistura "tendendo" à substância pura.]

Se a fração molar do gás 2 na solução líquida for dosada para cada uma das i situações, teremos determinado experimentalmente a dependência de x₂ sobre p₂. Com esses dados podemos construir o gráfico da função p₂ = f(x₂) ou de sua inversa, e o primeiro é mostrado na figura 26.

À medida em que p₂ aumenta, mais moléculas se dissolvem na fase líquida. A um certo momento, o número de moléculas de 1 vai se tornando desprezível em relação ao número de moléculas de 2. Nestas condições a fração molar do gás 2 torna-se praticamente igual a 1.0 (ou 100%). Se o gás 2 for um vapor teremos, neste caso, um sistema de duas fases constituídas praticamente por uma única substância pura. A pressão do sistema será então a pressão de vapor p^o₂ da substância pura. A partir deste momento, a pressão do sistema não mais se altera até que o mesmo se transforme totalmente em fase líquida. Se T for maior do que T_c, o momento em que n₁ torna-se desprezível coincidirá com a unificação das fases.

C-6 INTERVALO MATEMÁTICO. DIFERENCIAIS

A curva que exprime a função p = f(x) no intervalo entre x=0 e x=1, admite para um ponto C qualquer uma única reta tangente à mesma (figura 27). Através de C podemos traçar uma paralela ao eixo de x, a qual forma com a tangente um ângulo α. Estas duas retas determinam infinitos segmentos de reta d_pi perpendiculares ao eixo de x.

Cada um dos d_pi é chamado diferencial de p no ponto C. Para cada d_pi exixte um d_xi, chamado diferencial de x em C (vide figura 27), de tal forma que:

= tg α                (1-43)

A relação dp/dx é chamada coeficiente angular ou inclinação da reta tangente à função p = f(x) no ponto C.

A escolha de uma das diferenciais (dp ou dx) pode ser arbitrária; a outra, no entanto, assume um valor dependente dessa escolha. O estudo das diferenciais somente faz sentido quando elas são definidas duas a duas, respeitando a equação (1-43). Ao admitirmos o valor de uma delas, estaremos implicitamente assumindo o valor da outra.

Se em algum trecho a função p = f(x) for contínua e linear, a relação entre as diferenciais será constante para qualquer de seus pontos e igual à inclinação da reta que contém o segmento considerado (figura 28).

O encontro desta linearidade pode ser ocasional, frequente ou, mesmo, sempre presente, à medida em que fixamos algumas condições experimentais; e dependendo da relevância do achado, pode se constituir em uma lei natural. Para exprimirmos esta lei em equação matemática, podemos analisar o significado físico das constantes a e b da equação da reta (no caso, p = ax + b); ou então escolher diferenciais convenientes que possam estar relacionadas às propriedades que obedecem à lei considerada.

Podemos então admitir, para um ponto C_o, as diferenciais dp = Δp = p - p_o e dx = Δx = x - x_o, em que p_o e x_o são os valores das propriedades em C_o e p e x num outro ponto C qualquer do segmento em estudo. A lei pode ser então expressa da seguinte forma:

= =

ou

Δp = () Δx                (1-44)

em que dp/dx é uma constante, em geral dependente das condições experimentais (por exemplo, das substâncias 1 e 2 consideradas no item anterior) e é igual ao coeficiente angular do segmento estudado.

C-7 LEI DE HENRY

A experiência do item C-5, se efetuada para gases diversos, revelará um fato de extrema importância para o estudo da biofísica e bioquímica: Qualquer que seja o gás ou vapor estudado, nas vizinhanças de p_g = 0 (ou x_g = 0) a função p_g = f(x_g) é praticamente linear, o que está representado na figura 29 para três hipotéticos gases. p_g é a pressão parcial do gás considerado e x_g é a sua fração molar na fase líquida.

Essa vizinhança corresponde a soluções diluídas do gás considerado. O coeficiente angular varia de um gás para outro e também com a natureza do solvente considerado.

Como o segmento de reta encontrado experimentalmente nestes casos passa pela origem, podemos escolher este ponto como o C_o visto no item anterior (figura 28) e dar o tratamento matemático aí apresentado (equação 1-44):

p_g - p_{g_o} = (x_g - x_{g_o})

Como p_{g_o} = 0 e x_{g_o} = 0, substituindo-se estes valores e atribuindo-se à constante dpg/dxg o valor K_g, a equação se simplifica em:

p_g = K_gx_g                (1-45)

a qual é a expressão matemática da lei de Henry (1803), válida para soluções diluídas, cujo enunciado diz:

A solubilidade de um gás em um líquido é diretamente proporcional a sua pressão parcial.

A lei de Henry é válida também para soluções com vários gases como solutos, deste que todos estejam em concentrações diluídas. K_g depende da natureza do gás e do solvente, bem como da temperatura.

A lei de Henry é também uma lei aproximada e com campo de aplicação restrito. Seu significado real é melhor expresso pela equação:

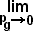
= K_g                (1-46)

A pressão parcial abaixo da qual podemos considerar, na prática, o limite satisfeito (p @ 0) e denominar a solução como diluída, utilizando então a expressão (1-45), depende das finalidades do estudo e do limite de confiabilidade das dosagens de p_g e x_g. O rigor matemático deve ser reservado para a conceituação de leis e propriedades. O bom senso e a teoria dos erros nos indicam quando ele pode ser deixado de lado.

O inverso de K_g é chamado fator ou coeficiente de solubilidade de gases em líquidos e representa a fração molar do gás para a pressão unitária:

x_g = p_g .

Quando p_g = 1 Þ x_g 1/K_g. Outros tipos de concentrações, além de x_g, podem ser utilizadas com finalidades semelhantes, fornecendo coeficientes de solubilidade dimensionalmente diferentes de 1/K_g.

C-8 GASES DISSOLVIDOS NO PLASMA SANGUÍNEO

Na bio-físico-química sanguínea, o gás carbônico e o oxigênio são convenientemente estudados em concentrações diversas da fração molar x. A lei de Henry deve então ser adaptada a essas condições.

a) Gás carbônico

A concentração plasmática de CO₂ é expressa em concentração molar. Para obter a expressão da lei de Henry devemos, então, efetuar a conversão de x_g em c_g (equação 1-8 em A-2), obtendo-se, de (1-45):

p_g = () c_g

ou

c_g = () p_g                (1-47)

ou

c_g = a_g p_g                (1-48)

em que a_g é o fator de solubilidade para a concentração expressa em concentração molar. a_g depende não apenas do gás considerado, do solvente e da temperatura,mas também do número de moles de outras substâncias presentes na solução. Tratando-se de soluções diluídas, n_t é praticamente igual ao número de moles do solvente e esta dependência torna-se desprezível

A pressão parcial do gás carbônico no plasma é expressa em mmHg, podendo-se também utilizar unidades MKS (ou SI) de pressão: 1 pascal = 1 Pa = 1 newton/m²; e a concentração molar em mol/l ou, mais frequentemente, em mmol/l (concentração milimolar).

Utilizando-se c_g em mmol/l e p_g em mmHg, o coeficiente de solubilidade para o gás carbônico no plasma sanguíneo, determinado experimentalmente, é igual a:

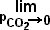
a_CO₂ = = 0.03 mmol/l.mmHg                (1-49)

à temperatura de 37°C. Esse valor pode ser utilizado para o cálculo de c_CO₂ quando a p_CO₂ é conhecida. Exemplo: Para a p_CO₂ = 40 mmHg temos:

c_CO₂ = 0.03×40 = 1.2 mmol/l

b) Oxigênio

A concentração de oxigênio é frequentemente expressa em vol/ml (v_O₂), a qual tem o significado de volume de O₂ liberado de 1 ml de solução, em condições especiais de pressão e temperatura da fase gasosa após a liberação do O₂. Em pressões próximas à atmosférica o comportamento do oxigênio aproxima-se do comportamento do gás ideal (figura 14) e podemos escrever para v_O₂:

v_O₂ =                 (1-50)

em que n_O₂ é o número de moles de O₂ dissolvidos em 1 ml de solução. Efetuando-se a conversão de n_O₂ em x_O₂ (equação 1-7 em A-2) e substituindo-se o valor encontrado em (1-50), temos:

n_O₂ = x_O₂n_t

v_O₂ =                 (1-51)

Substituindo-se o valor de x_O₂, obtido de (1-51), na expressão da lei de Henry (1-45):

p_O₂ = ()v_O₂

ou

v_O₂ = ()p_O₂ .

p e T são as condições em que o gás liberado de 1 ml da solução fornece o volume v_O₂. Se o coeficiente de solubilidade assim definido (n_tRT/K_gp) for determinado de forma que p = 1 atm e T = 273.15 K, ele recebe o nome de coeficiente de absorção de Bunsen (α_O₂) e seu valor é:

α_O₂ = ml/atm = ml/mmHg                (1-52)

Mais frequentemente v_O₂ é determinado a 37°C (310.15 K) e 1 atm, e o coeficiente de solubilidade S_O₂ nestas condições é:

S_O₂ = ml/atm = ml/mmHg                (1-53)

e a lei de Henry pode ser então expressa por:

v_O₂(37°C) = S_O₂p_O₂                (1-54)

Nota-se que v_O₂ é o volume do gás liberado em condições especiais de p e T as quais não têm nada a ver com a pressão e temperatura da solução.

A determinação experimental de S_O₂ para o plasma a 37°C é igual a:

S_O₂ = 0.00003 ml/mmHg                (1-55)

Mais frequentemente, utiliza-se para expressar a concentração de oxigênio o volume de O₂ liberado por 100 ml de plasma a 37°C e 1 atm de pressão. Este volume é representado como vol% de O₂. A equação (1-54) então fica:

vol% de O_2(37°C) = 100v_O₂(37°C) = 100S_O₂p_O₂

e substituindo-se o valor de S_O₂ dado em (1-55), temos:

vol% de O₂ = 0.003 p_O₂                (1-56)

observando-se que na falta de referência o gás foi liberado a 37°C e 1 atm de pressão e a temperatura do plasma prévia à dosagem era igual a 37°C. Desta forma, para uma p_O₂ igual a 100 mmHg teremos:

vol% de O₂ = 0.3 ml%

A relação entre S_O₂ e α_O₂ pode ser obtida dividindo-se (1-53) por (1-52):

S_O₂ / α_O₂ = 1.135

C-9 LEI DE RAOULT

A lei de Henry aplica-se a soluções diluídas, sendo útil no estudo das substâncias presentes em baixa concentração, comumente chamadas solutos. Seu caráter é mais geral que o adotado, sendo válida para qualquer solução diluída, fazendo-se a ressalva que, por ser uma lei com campo de aplicação restrito, o termo diluído não pode ser bem definido e para soluções diferentes, pode assumir conotações diferentes.

Uma solução é diluída quando todos os seus constituintes estão em concentração diluída, menos um, o solvente. Se efetuarmos o estudo da pressão de vapor p₁ de um líquido 1 volátil —ao qual chamaremos solvente— a partir de seu estado puro, adicionando-se gradativamenteΦ_2i moles de uma substância qualquer 2, verificaremos que à medida em que a fração molar do solvente vai diminuindo, sua pressão de vapor decresce até tender a zero, quando x₁ torna-se desprezível (figura 30).

Um fato que é sempre observado é que na região em que a solução é considerada diluída (x₁ ® 1, ou seja, próximo a C_o na figura 30) a função p₁ = f(x₁) é linear. Esta é exatamente a região em que a lei de Henry é válida para os solutos e seria interessante obtermos alguma relação para o solvente. Para esta região a equação (1-44) é válida na seguinte forma:

Δp₁ = () Δx₁

Escolhendo-se para C_o (conforme visto no item C-6) o ponto em que x₁ = 1 e, portanto, p₁ = p^o₁, a relação entre p₁ e x₁ para qualquer outro ponto C pertencente ao trecho linear será dada por:

p₁ - p^o₁ = () (x₁ - 1)                (1-57)

Outro dado de observação experimental é que a reta que contém o segmento linear da função (ou mais rigorosamente, a tangente à função no ponto C_o), passa pela origem do sistema. Consequentemente, se escolhermos dp_1i = p^o₁, dx_1i será igual a 1 (vide figura 30). Substituindo-se estes valores na equação (1-57) temos:

p₁ - p^o₁ = p^o₁ (x₁ - 1)                (1-58)

e simplificando a equação:

p₁ = p^o₁ x₁                (1-59)

e esta é a expressão da lei de Raoult (1886) que diz:

A pressão de vapor do solvente de uma solução diluída é igual à pressão de vapor do solvente puro, multiplicada pela fração molar do solvente na solução

Se quisermos relacionar o abaixamento da pressão de vapor com a fração molar do soluto, podemos utilizar a expressão (1-58), lembrando que (1 - x₁) = x₂. Portanto:

p^o₁ - p₁ = p^o₁ x₂

e havendo mais de um soluto:

p^o₁ - p₁ = p^o₁x_i

C-10 SOLUÇÃO IDEAL

Vimos em B-8 que o gás ideal é aquele que obedece as leis gerais dos gases, o que implica na ausência de forças de atração intermoleculares. Para um líquido esta obediência não faz sentido. Um líquido deixa de ser líquido à medida em que teorizamos tal situação, passando a se constituir num gás ideal condensado; e os dados obtidos em nada contribuiriam para o estudo de soluções reais. As soluções líquidas distanciam-se bastante deste tipo de idealidade; e as forças de coesão, além de estarem sempre presentes, representam uma característica importante das mesmas.

É possível estabelecer um critério de idealidade para soluções baseado justamente no caráter das forças de van der Waals. Num líquido puro, a igualdade entre as moléculas permite-nos admitir uma uniformidade entre as forças de coesão. Diluindo-se uma substância qualquer neste líquido, passamos a encontrar três tipos diferentes de interações moleculares:

soluto - soluto
soluto - solvente
solvente - solvente

Se as forças intermoleculares forem iguais, independentemente das substâncias químicas que interagem, chamaremos a solução de ideal.

Vimos em C-4 que para um líquido puro em contato com seu vapor, a tendência ao escape, medida pela pressão de vapor, iguala a tendência à permanência em grupo, provocada pelas forças de van der Waals. Numa solução real (vide C-5) a tendência ao escape da fase líquida de um de seus componentes diminui à medida que diminui o número de suas moléculas (figuras 26 e 30); esta dependência, no entanto, é complexa, traduzindo-se em funções p = f(x) de difícil equacionamento, exceto para os limites x ® 0 e x ® 1, em que tornam-se válidas, respectivamente, as leis de Henry e de Raoult (figura 31a).

Numa solução ideal a homogeneidade entre as moléculas faz com que o escape de uma delas para a fase gasosa seja independente da natureza das espécies químicas situadas em sua vizinhança. Aumentando-se ou diminuindo-se a concentração de uma determinada substância, a incidência de escape estará relacionada apenas a esta alteração no número de moléculas. E a tendência ao escape através de uma superfície fronteira líquido-gás, para uma dada espécie química, será diretamente proporcional à porcentagem de moléculas, desta espécie química, presentes nas vizinhanças desta superfície e em condições potenciais de escapar para a fase gasosa. Logo, a pressão de vapor será proporcional à fração molar, ou p = kx. Quando x for igual a 1 teremos o líquido puro e, portanto, p será igual à pressão de vapor p^o e igual a k. Logo, k = p^o (pois k é constante) e podemos escrever:

p = p^ox                (1-60)

a qual nada mais é senão a lei de Raoult, válida agora para qualquer valor de x (figura 31b). Como utilizamos o raciocínio para uma substância qualquer, a conclusão estende-se a todos os componentes da solução ideal. É costume definir a solução ideal como aquela que obedece a lei de Raoult para quaisquer concentrações de seus componentes.

Comparando-se os gráficos a e b da figura 31, nota-se que para a solução ideal as leis de Henry e de Raoult tornam-se coincidentes e, portanto, K_g (equação 1-45) iguala-se a p^o (equação 59 ou 60).

* * * * *

DHTML Menu By Milonic JavaScript