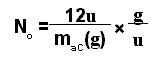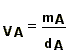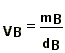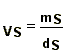Introdução à físico-química das soluções
Alberto Mesquita Filho
Página 1
Tema constante da parte introdutória da disciplina "Biofísica e
Bioquímica ministrada no curso de Biologia da USJT de 1977-83.
A. CONCEITOS GERAIS
A-1 SISTEMAS DISPERSOS
Imaginemos um sistema de duas ou mais fases, sendo uma contínua e as demais formadas por porções separadas, distribuídas uniformemente no seio da primeira. Tal sistema é chamado dispersão. Um exemplo multifásico do mesmo é o sangue, tendo como fase contínua, ou dispersante, a água plasmática, e como dispersos uma infinidade de elementos cujas unidades morfológicas apresentam dimensões que variam desde o nível de moléculas pequenas até o dos elementos figurados (figura 1). Quando as partículas dispersas têm diâmetros compreendidos entre 10-7 a 10-4 cm, a dispersão é chamada coloidal; quando os diâmetros são maiores do que o limite superior supracitado temos as dispersões grosseiras; e quando os diâmetros são menores que o limite inferior temos as soluções verdadeiras ou, simplesmente, soluções. Do exposto, podemos inferir que o sangue é uma dispersão complexa ou mista.
A classificação das dispersões, quanto ao tamanho das partículas dispersas, não é efetuada de forma arbitrária, mas está intimamente relacionada ao comportamento físico-químico das mesmas. As propriedades ópticas, a cinética das partículas, os fenômenos de superfície, tais como adsorção e/ou formação de camadas elétricas na interface dispersante-disperso, a permeabilidade através de membranas e a velocidade de sedimentação, quando sujeitas a ação de efeitos centrífugos, são exemplos de condições relacionadas ao tamanho das partículas dispersas; e a diversidade de comportamento está nitidamente relacionada aos limites apresentados acima para o diâmetro das mesmas.
O critério utilizado para caracterizar uma solução, conquanto correto do ponto de vista prático (partículas com diâmetros inferiores a 10-7 cm), não é isento de críticas, as quais residem no conceito de fase. "Fase é uma região de um sistema de composição química uniforme e propriedades físicas uniformes." Para individualizarmos uma tal região surge intrinsecamente em nossa mente a noção de superfície de contato ou fronteira entre duas fases. Num sistema em que todos os componentes têm dimensões moleculares pequenas torna-se difícil definir o que seja fronteira entre os componentes ou, até mesmo, definir qual seja o elemento dispersante. O conceito de fase contínua perde a sua razão de ser quando ao reduzirmos o nosso campo de observação, através da ampliação do objeto de estudo, nos deparamos com um imenso vazio de matéria, o único elemento realmente contínuo para um estudo destas proporções. Consequentemente, uma solução verdadeira não é verdadeiramente uma dispersão. Trata-se, na realidade, de uma "mistura unifásica ou homogênea de espécies químicas dispersas em uma escala molecular"; não existe dispersante e sim apenas dispersos. Os sistemas coloidais já se aproximam bastante de uma dispersão verdadeira, constituindo o que se chama mistura micro-heterogênea. Está claro que a distinção entre solução verdadeira e dispersão coloidal não é nítida, havendo sistemas de partículas dispersas com dimensões limítrofes (da ordem de 10-7 cm) e, portanto, de difícil caracterização. [Para uma abordagem crítica um pouco diversa daquela apresentada neste parágrafo, vide Homogeneidade e Incerteza].
É costume chamar o constituinte presente em maior quantidade numa solução, de solvente; e aos demais, de solutos. Nestas condições, o solvente não deve ser encarado como um dispersante mas sim como o disperso predominante. Este critério é totalmente arbitrário pois não há nada, além da quantidade, que os distinga. Nem sempre seguiremos esta regra.
A-2 CONCENTRAÇÃO DAS SOLUÇÕES
Um sistema homogêneo (solução) em equilíbrio fica bem definido após o conhecimento das nsq substâncias químicas que o constituem (análise química qualitativa), da pressão e temperatura (variáveis físicas quantitativas) e da quantidade de cada um de seus componentes (análise química quantitativa). Estas quantidades em geral são expressas em relação à quantidade de solução; outras vezes utiliza-se como referência a quantidade de um de seus constituintes que poderá então ser chamado solvente e em geral é o disperso predominante. Tais frações quantitativas são chamadas concentração.
Concentração é um termo genérico. Por si só não é uma entidade físico-química bem definida, faltando para tanto caracterizá-la dimensionalmente através da escolha das grandezas representativas das quantidades das substâncias químicas em questão. Por vezes é adimensional, representando, por exemplo, a relação entre a massa de soluto e a massa da solução; outras vezes é expressa em massa por volume; ou através de inúmeras outras maneiras. A escolha dimensional obedece a critérios baseados puramente na conveniência particular ao estudo que se pretenda efetuar. E esta conveniência particular em geral apóia-se no estabelecimento de equações simplificadas para expressar os princípios e leis do estudo em questão; ou então na maleabilidade operacional destas equações. Convém-nos adotar grandezas intimamente relacionadas ao número de moléculas das substâncias em estudo.
O número de moléculas de uma substância química presente num dado volume de solução, satisfaz parcialmente as necessidades de nosso estudo e poderia eventualmente ser utilizado como a concentração escolhida. Na prática sua utilidade é limitada por motivos de ordem operacional, a menos que se trabalhe com volumes de referência muito pequenos; a unidade de massa, em tal sistema, deveria ser da ordem da massa das moléculas constituintes, pois em unidades convencionais (grama por exemplo) trabalharíamos com números extremamente pequenos. Torna-se necessário então utilizarmos alguns artifícios para contornar o problema, criando-se um sistema de unidades a eliminar estes inconvenientes.
A massa molecular é expressa frequentemente em "unidade atômica de massa" (u). A unidade atômica de massa é "a massa igual a um doze avos da massa do átomo do isótopo estável do carbono com maior abundância relativa (98,9%)". A relação entre a massa maC deste átomo em unidades atômicas de massa pela mesma massa em gramas, nos fornece o fator de conversão No de gramas para unidades atômicas de massa:
maC(u) / maC(g) = 12u / maC(g) = 6.02 × 1023 u/g = No u/g (1-1)
No é o chamado número de Avogadro. Chamaremos de mol a "um conjunto qualquer que contenha o número de Avogadro em unidades elementares".
Exercício: 1) Com os dados acima apresentados, calcule a massa, em gramas, de um mol de átomos de carbono. 2) Calcule a massa, em gramas, de um mol de moléculas cuja massa molecular seja igual a 32u.Estamos vivenciando uma situação a clamar pela caracterização de uma "família de grandezas", a significar um "número de conjuntos de unidades elementares". Estas grandezas serão utilizadas com grande frequência na definição de estado de sistemas, ao lado de outras propriedades fundamentais como comprimento, massa, tempo e temperatura. Elas devem ter um valor numérico (quanto? = número puro), uma dimensão (o quê? = conjunto de moléculas, ou de átomos, ou de outras unidades elementares) e uma unidade "elementar" (a caracterizar quantos elementos compõem cada conjunto considerado unitário). Exemplos: a) 1 mol de fótons, também chamado 1 einstein, tem valor numérico igual a "1", dimensão a relacionar-se a "conjunto de fótons" e unidade igual a "mol". Portanto, um mol de fótons é igual a 1 conjunto de No fótons. b) 1 milimol de moléculas = 1 conjunto de No/1000 moléculas. c) 5 átomos = 5 conjuntos de 1 átomo.
Em nosso estudo, a grandeza que utilizaremos com maior frequência tem como unidade elementar a molécula e o conjunto mais utilizado é o mol. É costume chamá-la "número de moles", devendo-se lembrar no entanto que o mol é apenas uma de suas unidades e subentendendo-se que as partículas elementares são moléculas. Utilizaremos os seguintes símbolos:
Þ n para a grandeza;
Þ N para a dimensão; e
Þ mol (ou submúltiplos) para a unidade.Um mol de determinada substância química contém, por definição, No moléculas da mesma. A massa de um mol de uma substância química em gramas é chamada "molécula-grama" (M) e seu valor é obtido pelo produto de No pela massa da molécula (mm) em gramas:
M = Nomm(g) (1-2)
E a massa de n moles de uma substância química é, em gramas:
m = nM (1-3)
O valor de M depende apenas da massa da molécula da substância química considerada (mm), visto No ser constante. Atribuindo-se o valor 12u para maC(u), dado em (1-1), e substituindo-se No em (1-2) pelo seu valor em (1-1)
(1-4)
mostrando que M representa o número de vezes que a molécula de uma substância química qualquer pesa mais do que um doze avos do peso do átomo de 12C (a relação entre massas é numericamente igual à relação entre pesos). O valor numérico de M é frequentemente chamado peso molecular (PM), podendo-se dizer que a molécula-grama é o peso molecular expresso em gramas.
Para a concentração das soluções utilizaremos com maior frequência a concentração molar e a fração molar. A concentração molar (c) de uma substância em solução é uma relação entre o número de moles da substância (n) e o volume da solução (V):
(1-5)
Sua dimensão é NL-3. A unidade mais utilizada é o mol por litro, também conhecida por molaridade M da solução; solução 1 molar (1M) é a que contém 1mol por litro (1 mol/l). Outras unidades úteis:
1 mol/l = 103 mmol/l = 0.1 mol/100ml = 6.02×1023 moléculas/l (1-6)
A fração molar x de uma substância em solução é a relação entre o número de moles da mesma (n) e o número total de moles da solução (nt):
(1-7)
É uma grandeza adimensional e portanto sem unidades ou com unidades heterogêneas (por exemplo, moléculas/mol). Frequentemente é expressa em porcentagem. Exemplo: fração molar = 0.5 ou 50%. A conversão de x em c pode ser obtida igualando-se n de (1-5) e (1-7):
cV = xnt ou c = xnt/V (1-8)
A-3 DEFINIÇÃO DE ESTADO DE UM SISTEMA
Um sistema físico-químico é a parte do universo cujas propriedades físico-químicas estão sob investigação. Um sistema tem um estado definido quando cada uma das suas propriedades têm um valor definido. A solução constituída pelas substâncias A e B dispersas em um solvente S (figura 2) estará definida com o conhecimento do número de moles de A, B e S, da pressão e da temperatura. As demais propriedades e variáveis de estado têm um valor definido, podendo ser obtidas (vide tabela 1 abaixo) através de equações matemáticas de definição das variáveis e/ou de relações empíricas bem conhecidas entre as propriedades de estado (estudos anteriores) e/ou de tabelas especializadas fornecendo estas relações.
Dados: 1- Constituintes do sistema (figura 1): A, B e S
2- Numero de moles de A, B e S: nA, nB, nS
3- Pressão e temperatura
Calcular: cA, cB, cS e V (c = concentração molar)
V = VA + VB + VS (*)Conhecendo-se os constituintes do sistema (1), pode-se obter através de tabelas especializadas suas respectivas densidades (d) para a pressão e temperatura desejadas (3). E como d = m/V:
(*) VA e VB geralmente são desprezíveis
Tabela 1: Cálculo das demais variáveis de um sistema conhecendo-se o número de moles das substâncias constituintes do mesmo.
Ao invés do número de moles, o sistema da figura 2 poderia ser definido através das concentrações molares; neste caso, conhecendo-se a concentração molar de nSQ-1 substâncias, a concentração molar da substância restante será igual ao número de moles da mesma necessário para completar a unidade de volume da solução. A descrição completa do sistema requer no entanto a especificação do volume total do mesmo, assim como a natureza química da substância restante (tabela 2 - abaixo). Em cada caso, o número de variáveis químicas independentes é igual ao número de substâncias químicas nSQ.
Dados:
1- Constituintes do sistema (figura 1): A, B e S
2- Concentrações molares cA e cB
3- Volume do sistema: V
4- Pressão e temperatura
Calcular: nA, nB, nS e cS
nA = cAV Þ 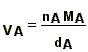
VS = V - (VA+VB) nB = cBV Þ 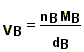
(*) VA e VB geralmente são desprezíveis
Tabela 2: Cálculo das demais variáveis de um sistema conhecendo as concentrações molares de nSQ-1 constituintes e o volume total.
É possível, em certos casos, descrever completamente a composição de uma solução através dos caracteres (natureza e concentração, por exemplo) de apenas algumas das substâncias químicas que a constituem. O número de variáveis químicas independentes é então menor do que nSQ e esta discordância deve-se a restrições impostas por fenômenos naturais regidos por leis físico-químicas ou por situações particulares, em que impõe-se a obediência a certos princípios. Torna-se necessário introduzir o conceito de "componentes independentes" ou simplesmente "componentes" de um sistema.
Componentes independentes —ou simplesmente componentes— de um sistema são os compostos químicos cujos caracteres devem ser especificados a fim de descrever qualitativa e quantitativamente a composição de um sistema homogêneo.Para o sistema da figura 2 o número de componentes é igual ao número de substâncias químicas (nC = nSQ). No estudo dos equilíbrios químicos verificaremos condições em que nC ¹ nSQ.
A-4 INTERVALO MATEMÁTICO. FUNÇÕES
"Domínio" de uma variável é o conjunto de valores que ela pode tomar. Exemplo: o domínio de m (m = massa de um sistema) pode ser pensado como igual ao conjunto do produto dos números naturais pela unidade elementar de massa.
Diz-se que uma variável y é função de x se a cada valor do domínio de x corresponder pelo menos um valor do domínio de y. Neste caso, e para explicitar a dependência, escrevemos y = f(x), ou y = g(x), ou y = F(x), ou y = G(x)... simbolizando a função. Exemplos:
- A massa de uma substância química A é função do número de moléculas (ou conjuntos de moléculas da mesma). Logo, mA = f(nA). Uma função pode ser expressa analiticamente, graficamente, ou através de tabelas e nomogramas. A relação entre massa e número de moles para uma dada substância química (mA = MAnA) é uma expressão analítica. A cada valor de nA corresponde um único valor de mA e, portanto, a função é unívoca.
- O peso molecular (PM) de uma substância química qualquer é função da massa molecular (mm), ou seja, PM = f(mm). Podemos escrever esta função sob a forma PM = kmm, em que k é uma constante igual a 12/maC (vide eq. 1-4 e definição de PM).
- A massa molecular (mm) de uma substância química natural é função de sua fórmula química (FQ) ou mm = g(FQ). O domínio de FQ está limitado pelo universo químico e o valor de mm, ou seja, g(FQ), poderia ser obtido, por exemplo, através de uma tabela especializada que fizesse a correspondência biunívoca entre mm e FQ.
- Se PM = f(mm) e mm = g(FQ), segue-se que PM = f[g(FQ)] ou PM = F(FQ). O peso molecular de uma substância química natural é função de sua fórmula química.
- A massa m de uma substância química qualquer é função do número de moles e também da molécula-grama (ou peso molecular): m = f(n, M). A equação (1-3) nos fornece a função m = nM. A cada par (n, M) corresponde um único valor de m e portanto a função é unívoca. O exemplo 1 é um caso particular em que fixamos M através da escolha da substância química A. A massa mA é função de uma variável, enquanto m é função de duas variáveis.
Clique na figura ao lado para continuar a ler o artigo Þ