Introdução à físico-química das soluções
Alberto Mesquita Filho
Página 3
B. SOLUÇÕES GASOSAS (continuação)
B-8 GASES REAIS
As leis gerais dos gases, embora traduzam com relativa precisão o comportamento dos mesmos em transformações que ocorrem entre estados não muito afastados das condições ambientais, não têm o caráter rigoroso que se pretendeu outorgá-las há alguns séculos atrás. Na realidade, são "leis aproximadas", verificadas apenas em certas circunstâncias; ou melhor dizendo, são leis com campo de aplicação restrito.
O comportamento dos gases reais não é tão simples quanto possa parecer pela análise dos itens precedentes; e os fatores responsáveis por esta complexidade são fundamentalmente três:
- As moléculas ocupam lugar no espaço;
- As moléculas apresentam forças de atração entre si (interação);
- As forças intermoleculares dependem da distância de separação entre as moléculas.
A primeira destas afirmações já implica numa limitação à lei de Charles: no zero absoluto de temperatura, o volume não pode ser igual a zero; logo, as retas da figura 6 não podem passar pela origem, e o gás real não obedece a lei de Charles (V = CT). À medida em que o volume molecular passa a ser desprezível em relação ao volume total do gás, este fator torna-se de pouca importância.
As forças de atração entre as moléculas têm resultante próxima a zero para moléculas situadas no interior do gás, porém esta deixa de ser nula para moléculas próximas às paredes do recipiente (figura 13). O efeito resultante se traduz na medida da pressão do gás. À medida que diminui o número de moléculas por unidade de volume, este efeito passa a ser pouco pronunciado, não só pela diminuição do número de moléculas que interagem mas também pela diminuição da própria força de atração entre as mesmas, a qual é dependente da distância de separação.
Os desvios entre o comportamento dos gases reais e aquele que seria de se esperar pela observância da lei dos gases, têm sido exaustivamente estudados à partir dos trabalhos de Amagat e Regnault, levados a efeito durante o século XIX. Um meio de se efetuar esta comparação pode ser obtido pela definição de um fator Z igual a:
(1-42)
Para um gás que obedeça as leis gerais dos gases, Z = 1, pois pV = nRT.
Observando-se experimentalmente o comportamento de um gás real através da medição de p, V e T, para um n conhecido, obtém-se, para a função Z = f(p), gráficos como aqueles apresentados na figura 14 para o hélio e o oxigênio, em que T e n são constantes. Nota-se, por este gráfico, uma tendência para Z aproximar-se de 1, à medida que a pressão diminui. O prolongamento do gráfico corta o eixo das ordenadas no ponto em que Z = 1. Ou seja, o comportamento dos gases reais aproxima-se da condição de obediência às leis dos gases à medida em que a pressão tende a zero. É importante perceber que nestas condições os três fatores limitantes, acima enunciados, tornam-se desprezíveis.
Esta tendência do gás real obedecer as leis gerais dos gases em determinadas condições, como por exemplo, para a pressão tendendo a zero, representa o sustentáculo mais consistente para que ainda hoje se consagrem as leis de Boyle, de Charles e de Avogadro. Com efeito, elas não são apenas leis aproximadas, nem tão somente leis com campo de aplicação restrito. Sua importância ultrapassa os limites de um laboratório, ganha um conteúdo teórico intuitivo sem precedentes e retorna às condições experimentais trazendo imenso auxílio ao estudo dos gases reais.
Em virtude desta importância, é costume definir como gás ideal ao gás hipotético que obedece as leis gerais dos gases.
B-9 INTERVALO MATEMÁTICO. LIMITES
a) Conceito intuitivo de limite
Em virtude do que foi exposto no item precedente podemos dizer que à medida em que a pressão de um gás tende a zero, o seu comportamento, frente a alterações em suas propriedades de estado, tende ao do gás ideal. Outras condições particulares a cada gás existem em que o comportamento dos mesmos aproxima-se ao do gás ideal. Em todos esses casos verifica-se que essa aproximação coincide com a obtenção de valores para Z cada vez mais próximos de 1. E o inverso é verdadeiro: sempre que Z tende a 1, o comportamento do gás tende ao ideal. É possível então definir o gás ideal como o limite para o qual tende o gás real, quando Z tende para 1. Simbolicamente podemos escrever:
Gás ideal =
(gás real)
Raciocínio análogo pode ser efetuado para expressões matemáticas. Desta forma, através da definição de Z (equação 1-42) podemos escrever:
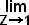
= R
Esta expressão encerra o comportamento dos gases reais e é, em síntese, o verdadeiro enunciado para a Lei Geral dos Gases. A lei de Boyle seria um caso particular em que n e T, sendo constantes, não afetariam intrinsecamente o resultado do limite, podendo serem colocados em evidência:
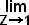
=
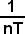
pV = R
ou
pV = nRT = B
Analogamente teríamos, para a lei de Charles:
= C
e para a lei de Avogadro:
= A
A figura 15 mostra o comportamento do oxigênio, num gráfico p versus pV [ou pV = f(p)], em condições de T e n constantes (T = 300K e n = 1 mol).
Existem duas regiões do gráfico, vizinhanças de Ao (p = 0) e de Ai (p = i), para as quais o comportamento do oxigênio a 300K aproxima-se do comportamento do gás ideal e, portanto, da obediência à lei de Boyle.
b) Conceito formal de limite
Analisemos com mais detalhes o gráfico da figura 15. Chamemos por Br (r de gás real) o valor assumido por pV = f(p). Nestas condições podemos dizer que o gráfico representa Br em função de p.
A figura 16 reproduz a figura 15 conservando apenas os detalhes que irão, por ora, nos interessar.
Dada uma vizinhança qualquer de um ponto qualquer A (a, b) do gráfico, corresponderá à mesma uma vizinhança Va de a no eixo de p e uma vizinhança Vb de b no eixo de Br. "Se para qualquer vizinhança Vb de b, por menor que ela seja, existir sempre em correspondência uma vizinhança Va de a, de tal forma que para todo p pertencente a Va e p ¹ a, o valor correspondente de Br pertencer a Vb, podemos dizer que:
b =
f(p)
ou seja, o limite da função de p [no caso Br = f(p)] para p tendendo a a é igual a b. No caso particular do ponto Ai da figura 15 temos:
Br = B
e como p ® i é equivalente a Z ® 1, e Br = pV, podemos escrever:
pV = B
O mesmo raciocínio pode ser efetuado para o ponto Ao da figura 15, levando a:
pV = B
em que p ® 0+ exprime o fato de p ser sempre positivo, ou seja, fisicamente p somente tende a zero pela direita do gráfico.
c) Aplicações práticas
Tomemos os valores das propriedades de estado obtidas experimentalmente para um gás qualquer, fixando-se duas variáveis (por exemplo T e n), e coloquemos os mesmos num gráfico pV/nT = f(p), como mostrado na figura 17, tanto para o hidrogênio quanto para o oxigênio. O prolongamento destes gráficos para a esquerda (p ® 0+) fornece, no ponto em que p = 0, o valor de R o qual, para todos os gases reais é:
R =
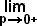
= 0.08206
A partir do valor de R pode-se obter uma expressão para o volume do gás ideal:
Vid = 0.08206
válida para T em K, p em atm e fornecendo Vid em litros. Tratando-se de uma expressão para o gás ideal, é válida para qualquer pressão e temperatura. Para o volume molar do gás ideal teremos:
Vid =
=
e nas condições normais de pressão (1 atm) e temperatura (273.15 K) seu valor será:
Vid = (0.08206 × 273.15) / 1 = 22.414 litro/mol.
Outra aplicação prática do comportamento limite dos gases reais reside na determinação do peso molecular de gases e substâncias voláteis. Com efeito, sendo M constante (ausência de reações químicas), podemos escrever:
R =
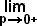
=
= M
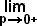
ou
M = R
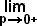
=
A figura 18 mostra o gráfico do tipo
= f(p) para uma massa fixa de oxigênio a temperatura constante e igual a 300K. O prolongamento deste gráfico para a condição em que p = 0 fornece o valor de MO2 e, portanto, o peso molecular do oxigênio.
C. SOLUÇÕES LÍQUIDAS
C-1 GENERALIDADES
Soluções líquidas são aquelas em que o disperso presente em maior quantidade é um líquido. Os outros dispersos podem ser sólidos, gases, vapores ou mesmo outros líquidos. As quantidades relativas dos dispersos podem, em teoria, assumir proporções as mais diversas. Na prática isto nem sempre é possível, pois dependendo das substâncias consideradas, a miscibilidade em certas condições não é total. Consequentemente, uma ou mais substâncias em maior ou menor grau se separa da solução, constituindo outras fases.
Consideraremos inicialmente apenas soluções binárias, constituídas por duas substâncias totalmente miscíveis (miscíveis em todas as proporções) e das quais uma seja líquida. A partir desse estudo, e sempre que possível, estenderemos as considerações para soluções mais complexas.
C-2 LIQUEFAÇÃO E VAPORIZAÇÃO
Antes de entrarmos propriamente no estudo das soluções líquidas, vejamos alguns conceitos fundamentais, de grande importância para o estabelecimento de relações úteis, e que situam-se exatamente na fronteira entre o estudo que ora iniciamos e o que terminamos de apresentar.
Numa transformação isotérmica tipo Boyle, verificamos nos itens precedentes que os gases reais comportam-se de forma diferente do gás ideal. Estudamos diferenças intrínsecas ao estado gasoso. Outras diferenças existem as quais estão relacionadas a transformações de estado. O gás ideal somente "existe" no estado gasoso. O gás real, pelas mesmas razões que o afastam do comportamento ideal, pode em determinadas condições transformar-se em líquido ou sólido.
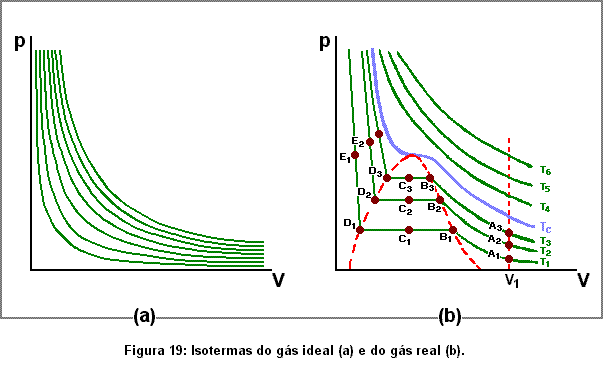
Construindo-se gráficos representativos de transformações tipo Boyle (figura 19), chama a atenção que, para o gás real, existe uma temperatura Tc abaixo da qual a contração isotérmica, a partir de um volume V1, atinge um ponto Bi (i = 1, 2, 3, ...) onde uma nova contração volumétrica, até um ponto Di, não se acompanha de variação da pressão. A partir de Di a pressão se eleva abruptamente para a mínima diminuição de volume.
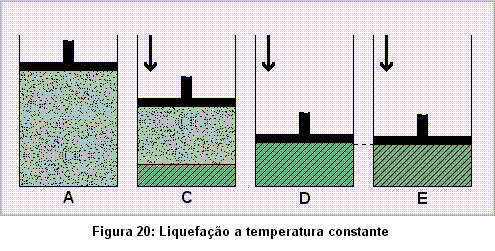
Se efetuarmos a experiência descrita, verificaremos que em Bi inicia-se a liquefação e entre este ponto e Di temos uma mistura de duas fases, líquido e gás, de uma mesma substância química. A partir de Di o gás original estará completamente liquefeito (figura 20).
Acima de Tc, a substância química considerada somente existe na forma de gás. Abaixo de Tc podemos considerar três regiões (figura 21)
conforme exista líquido, gás, ou uma mistura dos dois. Tc é a chamada temperatura crítica e seu valor depende da substância química considerada. É costume chamar vapor ao gás com temperatura abaixo da temperatura crítica.
A experiência inversa, iniciando-se num ponto Ei da figura 19 e promovendo-se a expansão isotérmica do líquido, nos leva ao conceito de vaporização. Se efetuarmos a medida da pressão do sistema através de um manômetro (figura 22), verificaremos que durante a vaporização ela não varia. Dependendo da temperatura considerada na qual a experiência é realizada (lembrar que T permanece constante) e também da natureza do líquido, a pressão na qual coexistem líquido e vapor assume valores os mais diversos, chegando mesmo em alguns casos, a atingir níveis próximos a zero. Esta pressão, dependente apenas da temperatura e da substância química, quando no estado puro, é chamada pressão de vapor do líquido considerado.
A importância da pressão de vapor ficará cada vez mais patente à medida em que formos evoluindo no estudo das soluções líquidas.
C-3 LÍQUIDOS VOLÁTEIS
Na realidade todos os líquidos são voláteis. No entanto, para líquidos que apresentam pressão de vapor muito baixa, a vaporização chega a ser praticamente nula em expansões volumétricas rotineiras, como aquela apresentada na figura 22. Nestes casos a fase gasosa não difere muito do vácuo ideal, o que está de acordo com o fato de a pressão ser próxima a zero.
O conceito de líquido volátil, como é utilizado na prática, é um conceito comparativo, ou seja, um líquido é volátil, em relação a outro, quando o grau de vaporização do segundo for desprezível em relação ao do primeiro, para condições experimentais semelhantes.
Para estudos nos quais as propriedades físicas intensivas não se distanciam muito das condições ambientais, podemos dizer que líquido volátil é aquele que tem pressão de vapor não desprezível em relação à pressão atmosférica, à temperatura ambiente.
O mercúrio é um líquido praticamente não volátil e este fato tem sido aproveitado para a medida da pressão de vapor de líquidos voláteis. O vácuo formado por uma coluna de mercúrio superior a 76 cm de altura, vaporiza um líquido volátil adicionado da forma mostrada na figura 23, até que a pressão da câmara acima do mercúrio atinja o valor da pressão de vapor do líquido considerado. A partir deste momento inicia-se a formação de uma camada líquida. Neste momento podemos efetuar a leitura da altura da coluna de mercúrio (h) e calcular a pressão de vapor através da fórmula
p = ho - h cm Hg
em que ho representa a altura inicial da coluna de mercúrio, ou a pressão atmosférica local em cm de Hg.
C-4 SIGNIFICADO FÍSICO DA PRESSÃO DE VAPOR
Se um gás real qualquer estiver em condições de pressão muito reduzida, próxima a zero, seu comportamento será praticamente igual ao do gás ideal na mesma pressão e temperatura. O volume ocupado pelas moléculas é praticamente nulo em relação ao volume ocupado por todo o gás; e a distância entre as moléculas é tão grande que podemos seguramente dizer que as forças de atração intermoleculares (forças de van der Waals) não afetam o comportamento do gás. As moléculas se movem com liberdade total e com uma energia cinética média intimamente relacionada à temperatura do gás.
À medida que reduzimos o volume do gás, mantendo a temperatura constante, as moléculas vão se tornando cada vez mais próximas. Macroscopicamente isto se reflete num aumento da pressão. Nestas condições, as forças de van der Waals vão se tornando cada vez mais intensas e as moléculas vão perdendo sua individualidade e apresentando um movimento que, embora ainda desordenado, obedece as condições impostas pelas leis das probabilidades; e para uma molécula qualquer, o mais provável é, qualquer que seja a sua trajetória, defrontar-se e interagir com outras moléculas. Modifica-se assim a sua trajetória original e a molécula parte para novos confrontos, cada vez mais frequentes à medida em que o volume total do gás diminui.
A um certo momento, a energia cinética molecular, responsável pelo movimento desordenado das moléculas, torna-se insuficiente para que estas escapem à ação de suas vizinhas; as forças de van der Waals atingem um valor elevado o bastante para que a tendência à fuga iguale a tendência à aproximação. Alguns grupos de moléculas se condensam, passando a constituir a fase líquida. A contração de volume torna-se agora isobárica, pois os grupos de moléculas que se condensam vão compensando a diminuição total de volume. Enquanto houver vapor em condições de se condensar, o número de moléculas por unidade de volume em cada uma das fases não se altera e, consequentemente, a pressão permanece constante. Deixando de existir o vapor, a pressão volta a ser novamente função do volume. Justifica-se então o termo pressão de vapor.
A pressão de vapor de um sistema constituído por uma substância pura representa, para a fase gasosa, uma medida da tendência à aproximação (energia de interação) a qual, nestas condições, iguala a tendência à fuga (energia cinética). Compreende-se então a sua dependência à temperatura mostrada na figura 24. Quanto maior for a temperatura, maior será a tendência à fuga e mais próximas deverão estar as moléculas para que o equilíbrio se processe. Consequentemente, maior será a pressão de vapor.
Para sistemas situados acima da temperatura crítica, a condensação (redução brusca de volume) não ocorre. A energia cinética molecular nestas condições é de tal ordem que o equilíbrio fuga-aproximação se estabelece quando o sistema já se encontra condensado. O limite entre gás e líquido não é nítido e a pressão em que tal fenômeno se processa não é macroscopicamente detectável. Embora o significado físico do processo permaneça, sua importância cai a um nível secundário. Um sistema próximo destas condições é chamado fluido.
Na fase líquida as moléculas também estão sujeitas a "tendências conflitantes": a tendência ao escape e retorno à fase gasosa; e a tendência à permanência em grupo, provocada pelas forças de coesão de van der Waals. Durante a vaporização a pressão de vapor representa a pressão na qual as moléculas iniciam o escape de sua estrutura condensada para constituir a fase gasosa. A pressão de vapor é, portanto, considerada, no estudo dos líquidos, como uma medida da tendência que uma determinada espécie química tem de escapar para a fase de vapor.
O equilíbrio estabelecido entre a fase de vapor e a fase líquida é a condição em que o número de moléculas que escapam para a fase de vapor é igual ao número de moléculas que se condensam no intervalo de tempo considerado.
Clique na figura ao lado para continuar a ler o artigo Þ