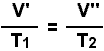Introdução à físico-química das soluções

Alberto Mesquita Filho
 
 
 Página 2

B. SOLUÇÕES GASOSAS

B-1 GENERALIDADES

As soluções gasosas são aquelas em que o disperso em maior quantidade é um gás. Estudaremos neste tópico apenas as soluções gasosas em que todos os seus constituintes são gases; e chamaremos estas soluções de misturas de gases visto que quase sempre tais misturas constituem sistemas homogêneos ou unifásicos. Como exceção a esta regra temos misturas de gases situadas num campo de força gravitacional, particularmente quando a altura é grande o bastante para que não se possa desprezar este efeito; assim, a fração molar dos gases da atmosfera é função da altitude e, portanto, a atmosfera não constitui uma solução.

As propriedades de estado mais utilizadas para descrever as misturas de gases são em número de n_C + 4 e estão representadas na tabela 3; n_C é o número de componentes independentes e neste capítulo será sempre igual ao número de substâncias químicas n_SQ.

P.E.		Quantitativas ou mensuráveis n.° = 4		Extensivas: massa e volume
				Intensivas: pressão e temperatura
		Qualitativas ou não mensuráveis n.° = nC		Componentes do sistema

Tabela 3: Propriedades de Estado (P.E.) utilizadas no estudo dos gases.

As equações empíricas que correlacionam as propriedades de estado constituem as expressões matemáticas das leis gerais dos gases ou equações de estado do sistema considerado. Iniciaremos o estudo para situações em que o número de componentes é igual a um, generalizando-o a seguir para as misturas de gases propriamente ditas.
 

B-2 LEIS GERAIS DOS GASES

a) Lei de Boyle:

A primeira destas leis foi estabelecida por Robert Boyle em 1662 e diz que "o volume de uma dada massa de gás mantida a temperatura constante é inversamente proporcional à pressão":

V = B/p                (1-9)

em que V é o volume, p é a pressão e B é uma constante.

Se V é uma função de p (lei de Boyle), o que pode ser representado por V = f(p), então p é função de V, ou seja, p = g(V). Esta função g é chamada função inversa de f e pode ser representada por p = f^-1(V). A expressão matemática para esta função inversa pode ser obtida de (1-9):

p = B/V                (1-10)

Esta expressão pode ser parcialmente entendida desde que se aceite os fundamentos da teoria cinética dos gases: "As moléculas movem-se ao acaso e em linha reta e ao atingirem a parede do recipiente que as contém, sofrem colisões perfeitamente elásticas."

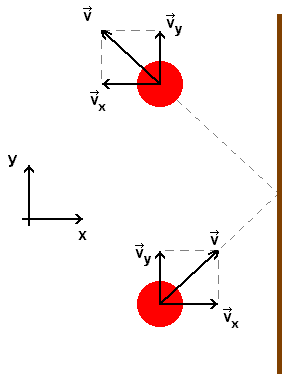
Durante o intervalo de tempo em que molécula e parede ficam em contato, a molécula sofre uma variação na velocidade, de forma que ao se desligar da parede a direção e o sentido desta velocidade acham-se alterados (figura 3a). Neste intervalo de tempo a partícula fica sujeita a uma aceleração, a qual é a responsável pela mudança na componente v_x da velocidade. Molécula e parede comportam-se como uma mola que é comprimida e a seguir volta a seu formato original. Logo, a parede do recipiente exerce uma força sobre a molécula durante o tempo de contato molécula-parede. Pelo princípio da ação e reação, esta mesma força é exercida, durante o mesmo tempo, pela molécula sobre a parede.

A figura 3b é um gif animado a ilustrar, em câmara lenta, a ação exercida por uma parede, rígida e fixa, sobre uma bola elástica em movimento inercial e a chocar-se com a parede; a flecha aí representada durante o contato bola-parede, representa a força exercida pela parede sobre a bola. Este modelo presta-se a simular o que ocorre em nível molecular e ainda que existam fatores outros, pode-se, num primeiro estudo, desprezá-los a bem da simplicidade.

a		b
Figuras 3a e 3b - Explicação no texto

A força total (ou resultante) exercida pelas moléculas do gás, num instante t, sobre a unidade de área do recipiente, é a pressão p. Ou seja, p = F/A, em que F é a força resultante agindo sobre uma área macroscópica A. Estatisticamente p independe da área A escolhida para a medida de F e do tempo considerado. Aumentando-se o volume V do sistema o percurso que cada molécula deve efetuar, até chocar-se com a parede do recipiente, aumenta, diminuindo o número de colisões na unidade de tempo e, consequentemente, diminuindo a pressão p, o que está em acordo com a equação (1-10).

b) Lei de Charles:

A lei de Charles (1781) diz que "o volume de uma massa fixa de um gás, mantido a pressão constante, é diretamente proporcional à temperatura absoluta":

V = CT                (1-11)

em que T é a temperatura absoluta e C é uma constante.

A lei de Charles, à luz da teoria cinética dos gases, permite-nos conceituar a temperatura de uma forma diferente da tradicional ou clássica. Pela lei de Charles, mantendo-se a massa, a espécie química, o estado gasoso e a pressão, e aumentando-se o volume, a temperatura deve aumentar. Ora, mantendo-se a espécie química, a massa molecular m_m permanece constante e, portanto, a molécula-grama (M) não se altera (equação 1-2). Mantendo-se a massa, o número de moléculas (ou de moles) permanece constante (equação 1-3). Aumentando-se o volume, o percurso que cada molécula deve efetuar até chocar-se com a parede do recipiente aumenta. Se a velocidade molecular permanecesse constante, o número de colisões por unidade de tempo diminuiria e seria de se esperar uma queda de pressão. Como a pressão permanece constante, admitimos que a velocidade molecular aumenta. Percebemos aí uma relação entre velocidade molecular e temperatura, o que nos induz a pensar em temperatura absoluta como uma medida da energia cinética molecular média de um conjunto de moléculas. O conceito de temperatura absoluta torna-se claro e o zero absoluto representaria o repouso molecular (translacional).

Tanto a lei de Boyle quanto a lei de Charles referem-se a transformações que ocorrem em um sistema gasoso fechado, ou seja, no qual a massa não atravessa as fronteiras do mesmo.

c) Lei de Avogadro:

A lei de Avogadro (1811) diz que "volumes iguais de gases de natureza diversa, nas mesmas condições de pressão e temperatura, contém o mesmo número de moléculas". Da forma como está exposta, a lei de Avogadro refere-se à comparação entre sistemas gasosos. Interessa-nos explorá-la de uma forma mais ampla, qual seja, adaptá-la a determinadas transformações que possam ocorrer num sistema gasoso constituído por um componente (não obrigatoriamente fixo). Para tanto, vamos antes definir volume molar.

Volume molar V é o volume ocupado por um mol de uma substância química qualquer. O volume total pode ser expresso por:

V = nV                (1-12)

Para um sistema homogêneo, V é uma propriedade intensiva e, portanto, independente do volume considerado.

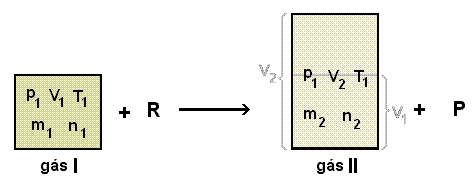
Imaginemos agora um sistema constituído por um gás I em equilíbrio. Num determinado momento adicionamos um reagente R de tal forma que a reação entre I e R resulte na extinção completa de I e na formação de um gás II mais um produto de reação P (figura 4).

Figuras 4 - Explicação no texto

A obtenção do gás II na sua forma pura (eliminando-se P e o resíduo de R), nas condições originais de pressão e temperatura (p₁ e T₁), nos fornecerá um volume V₂ não obrigatoriamente igual a V₁. Seja, por exemplo V₂ > V₁. Pode-se imaginar o sistema agora constituído pelo gás II, como sendo formado por duas frações: uma com o volume igual a V₁ e outra com o que falta para V₂ (figura 4, vide representações volumétricas em cinza). Pela lei de Avogadro, o número de moles (ou de moléculas) contido na fração de volume V₁ é igual a n₁. O volume molar do gás II (V_II) será igual nas duas frações, podendo ser determinado, com o auxílio da equação (1-12), tanto através da fração V₁ como do volume total V₂ do sistema: V_II = V₁/n₁ ou V_II = V₂/n₂. Igualando estas duas expressões chegamos a:

                (1-13)

Substituindo n₁ e n₂ por valores obtidos através da equação (1-3):

                (1-14)

As expressões (1-13) e (1-14) podem ser escritas na forma:

V = An       e       V = Am/M                  (1-15)

em que A é uma constante. Podemos então dizer que "o volume de um sistema gasoso constituído por um único componente (não obrigatoriamente fixo) e mantido a pressão e temperatura constantes, é diretamente proporcional ao número de moles". Esta nada mais é senão uma outra maneira de enunciarmos a lei de Avogadro, agora em analogia com as leis de Boyle e Charles.

A equação (1-14) subentende como variáveis de estado a massa e o componente. Diferentemente das expressões das leis anteriores vemos que: 1.°) Se a massa é variável, pelo princípio da conservação da matéria o sistema deve ser aberto (a massa atravessa as fronteiras do mesmo); 2.°) Se o componente é variável, deve ter ocorrido uma reação química, a menos que o transporte de massa tenha sido total (substituição de I por II). Vimos na tabela 3 que o componente é uma propriedade de estado qualitativa; vemos agora que a molécula-grama (M) é uma variável de estado que representa quantitativamente o componente.

Um exemplo da reação da figura 4 é a oxidação da glicose formando gás carbônico e água:

C6H12O6     +     6O2     ————>     6CO2     +     6H2O

Neste caso particular, n₁ é proporcional a n₂, pois os gases reagente e produto transformam-se na proporção de 1:1 moléculas; portanto V₁ será igual a V₂. Verifica-se pelo exame desta reação que ocorre um transporte de matéria para o sistema gasoso, o que se traduz por um ganho em carbono.
 

B-3 INTERVALO MATEMÁTICO. GRÁFICO DE UMA FUNÇÃO

A temperatura em grau Celsius é função da temperatura absoluta:

t = f(T) = T - 273.15

e a função inversa será:

T = f^-1(t) = t + 273.15.

Numa transformação tipo Charles temos:

V = g(T) = CT.

Logo:

V = g[f^-1(t)] = C( t + 273.15).

Vamos então estudar graficamente um caso particular dessa expressão, aquele em que C = 0.6. A expressão será então:

V = 0.6t + 164                (1-16)

O gráfico de uma função definida por V = F(t) é uma representação pictórica da função, o que pode ser obtido demarcando-se, num sistema de coordenadas retangulares, os pontos definidos pelos pares de números (t, V) ou [t, F(t)]. Se (1-16) for a expressão matemática para essa função, o gráfico obtido será aquele mostrado em vermelho na figura 5, ou seja, uma reta. A função é dita linear.

Uma variável é função linear de outra quando ambas estão relacionadas por uma função da forma

V = at + b                (1-17)

em que a e b são constantes. Para o exemplo da figura 5, a = 0.6 e b = 164.

A equação (1-17) e a figura (1-5) nos mostram o significado de a e b:

1. b é o valor de V quando t é igual a zero;
2. a é igual à relação (V-b)/t e verificamos que para qualquer ponto P do gráfico é possível construir um triângulo retângulo tal que (V_i-b)/t_i, em que i = 1, 2, 3, ..., seja a relação entre o cateto oposto e o cateto adjacente ao ângulo α formado entre a reta representativa da função e uma paralela ao eixo de t (vide figura 5).

Portanto:

a = tg α                (1-18)

e a é chamado coeficiente angular ou inclinação da reta V = at + b.

A função de Charles V = CT é um caso particular de função linear do tipo V = aT + b, em que b = 0 e a = C. A figura 6 mostra o gráfico de várias destas funções, que diferem entre si pelo valor de C, ou seja, pelo coeficiente angular. Como b = 0, quando T = 0 teremos V = 0 e, portanto, todas as retas passam pela origem.

Como a transformação de Charles é a pressão constante, é costume chamar tais retas de isóbaras, correspondendo cada uma delas a um valor de P.
 

B-4 EQUAÇÃO GERAL DE ESTADO

As leis gerais dos gases nos fornecem três equações de estado úteis para o estudo de transformações de estado particulares. Interessa-nos obter relações entre propriedades de estado para uma transformação qualquer. A situação mais geral é a transformação de um sistema constituído por um gás nas condições p₁, V₁, T₁, m₁ e M₁ em outro também constituído por um gás, porém nas condições p₂, V₂, T₂, m₂ e M₂. A maneira como a transformação ocorreu não nos interessa. Interessa apenas estabelecer relações entre as propriedades no estado inicial (1) e no estado final (2). Para tanto podemos utilizar um artifício supondo que a transformação global tenha ocorrido em três etapas a respeitarem, em cada uma delas, uma das três leis gerais que estudamos no item B-2. A figura 7, apresentada a seguir, fornece esse raciocínio de maneira esquemática.

	p1       V1 T1 m1       M1		?	p2       V2 T2 m2       M2
	Lei de Boyle isotérmica isomássica isoquímica p1V1 = p2V'				Lei de Avogadro isobárica isotérmica
	p2       V' T1 m1       M1		Lei de Charles isobárica isomássica isoquímica	p2       V'' T2 m1       M1
	Figura 7: À procura da equação geral de estado.

Substituindo o valor de V' dado pela lei de Boyle como apresentado na figura 7, na expressão da lei de Charles, e substituindo-se o V'' assim obtido na expressão da lei de Avogadro, chegamos a uma relação entre todas as variáveis de estado consideradas para os estados 1 e 2:

Esta é a equação de estado procurada. Lembrando que n = m/M, e generalizando a expressão para um estado qualquer, temos:

ou, como é mais conhecida:

pV = nRT                (1-19)

em que R é a chamada constante dos gases.

Lei de	Variáveis	Constantes	Equação de Estado
Boyle	p, V	T, m, M	pV = mRT/M = B
Charles	V, T	p, m, M	V/T = mR/pM = C
Avogadro	V, m, M	p, T	VM/m = RT/p = A
Tabela 4: Casos particulares da equação geral de estado.

As três leis gerais dos gases estão implícitas na equação (1-19) e os significados matemáticos das constantes B, C e A estão representados acima na tabela 4. B, C e A são constantes apenas para transformações específicas e seu valor depende do estado inicial. Já havíamos admitido esta dependência para C no item B-3, ao discutir a figura 6. Vemos agora, pela tabela 4, que C é uma função de três variáveis: C = f(m, p, M). A e B são também funções de estado dadas por: A = g(T, p) e B = F(m, T, M).
 

B-5 SIGNIFICADO E VALORES DE R

R é independente do estado e seu valor é constante para qualquer das transformações que consideramos até aqui. Em virtude da importância que assumirá em nosso estudo, convém que efetuemos a análise de seu significado físico. Para tanto consideremos um gás contido num recipiente dotado de um êmbolo móvel e em equilíbrio graças à presença de um corpo de massa m apoiado sobre o mesmo (figura 8a ao lado). O gás exerce uma força sobre o êmbolo igual a:

|F_gás| = p₁A

em que A é a área do êmbolo; e m exerce uma força sobre o êmbolo igual a:

|F_m| = mg

em que g é a aceleração da gravidade. Considerando-se a massa do êmbolo desprezível e estando o mesmo em equilíbrio,

|F_gás| = |F_m|.

Portanto:

p₁A = mg                (1-20)

Se o gás sofrer uma transformação isobárica tipo Charles (figura 8b) até um volume V₂, o corpo de massa m será deslocado para uma posição mais alta. Diremos que m ganhou energia potencial ΔEP, tal que

ΔEP = EP₂ - EP₁

Esse ganho em energia potencial é igual a

ΔEP = mgh                (1-21)

Sob o ponto de vista termodinâmico, o sistema (gás) realizou um trabalho W, pois um elemento de massa m exterior ao mesmo ganhou energia potencial. A medida do trabalho realizado pelo gás é igual à variação em energia potencial experimentada por m. Logo:

W = mgh.                (1-22)

[Se o leitor estiver tendo dificuldades em acompanhar este capítulo talvez fosse interessante consultar alguns dos tópicos listados em "Considerações sobre irreversibilidade e entropia — Um curso de introdução à termodinâmica pela internet".]

Comparando-se (1-20) com (1-22) temos:

W = p₁Ah = p₁(V₂ - V₁) = p₁ΔV.                (1-23)

Aplicando-se a equação geral de estado à transformação realizada, temos:

Estado 1:                p₁V₁ = nRT₁                (1-24)

Estado 2:                p₁V₂ = nRT₂                (1-25)

Subtraindo (1-24) de (1-25):

p₁ΔV = nRΔT

e para R teremos:

R =                 (1-26)

Substituindo p₁ΔV pelo valor dado em (1-23):

R =                 (1-27)

No caso particular em que n = 1 mol e ΔT = 1K:

R W

ou seja, R é numericamente igual ao trabalho efetuado por 1 mol de um gás, numa expansão isobárica tipo Charles, consequente ao aumento na temperatura de 1 kelvin.

O valor de R pode ser obtido através do seguinte raciocínio: O volume ocupado por um gás nas condições normais de pressão (1 atm) e temperatura (0°C = 273.15 K), pela lei de Avogadro depende apenas do número de moles. Para um gás que obedeça as leis gerais dos gases, este volume é igual a:

V = 22.414n litros

em que 22.414 litros é o volume molar nas condições normais de pressão e temperatura (CNPT) como veremos no item B-9c. Resolvendo-se a equação geral dos gases (1-19) para 1 mol, nestas condições, temos:

R = (1atm×22.414litro)/(1mol×273,15K) = 0.08206 (atm×litro)/(mol×K)

Outras unidades úteis são:

R = 8.3144×107 (g×cm2)/(seg2×mol×K)                [erg/mol×K]

R = 8.3144 (kg×m2)/(seg2×mol×K)                [joule/mol×K]

R = 1.9872 (cal)/(mol×K)

A transformação de pressão em atmosferas para unidades fundamentais pode ser efetuada através do conhecimento que a pressão de 1 atm equilibra uma coluna de mercúrio de 760 mm de altura. Logo:

1 atm = 76 cm Hg.

A pressão exercida por uma coluna de mercúrio pode ser dada por:

p_Hg = F/A = mg/A = dVg/A = dgh                (vide figura 9)

em que d é a densidade do mercúrio (d = m/V) e h é a altura da coluna (h = V/A). Portanto, a pressão exercida por uma coluna de mercúrio de 76 cm será:

1 atm = 76 cm de Hg = 13.6 g/cm3 × 980cm/seg2 × 76cm =

           = 1 012 928 g/cm×seg2                (bária)

cálculo este que é aproximado em virtude das aproximações efetuadas para d (13.6 g/cm3) e g (980 cm/seg2).

O valor de R em unidades térmicas pode ser obtido através da igualdade:

1 cal = 4.184 joule.
 

B-6 MISTURA DE GASES

Consideremos um conjunto de s gases de natureza distinta, com massas variáveis, porém à mesma temperatura T e ocupando um volume igual V (figura 10).

	p1    m1    M1 V       T 1		p2    m2    M2 V       T 2	...	ps    ms    Ms V       T s
Figura 10: Conjunto de s gases de natureza diversa, a T e V iguais.

A pressão desses gases será dada pela equação (1-19):

p₁ =             p₂ =    ...   p_s =                 (1-29)

ou, genericamente:

p_i =                 (1-30)

em que i = 1, 2, 3, ..., s.

Se os gases 1, 2, ..., s forem misturados, de tal forma que a mistura ocupe o volume V na temperatura T (figura 11), e admitindo-se a não ocorrência de reações químicas entre os mesmos, a pressão p da mistura será dada pela lei de Dalton (1820): "A pressão exercida por uma mistura de gases é a soma das pressões que cada um exerceria se ocupasse, sozinho, o volume da mistura na temperatura da mistura." Logo:

p = p₁ + p₂ + ... + p_s                (1-31)

	p      V      T m1   m2 ... ms M1   M2 ... Ms 1 + 2 +...+ s		Conservação da Matéria:           m = m1 + m2 + ... + ms =      Lei de Dalton:           p = p1 + p2 + ... + ps
Figura 11: Mistura de gases de natureza diversa.

Substituindo p₁, p₂, ..., p_s, em (1-31), pelos valores dados nas equações (1-29):

p = n₁ + n₂ + . . . + n_s

ou

p = (n₁ + n₂ + ... + n_s)                (1-32)

ou

pV = RTn_i                (1-33)

a qual é a equação geral para uma mistura de gases.

A lei de Dalton, associada a dados de ordem experimental, permite a introdução de um novo conceito em nosso estudo: o de pressão parcial. O enunciado da lei já permite a aceitação de um conceito abstrato para pressão parcial: seria a pressão p_i que o gás i exerceria "se" ocupasse isoladamente o volume da mistura na temperatura da mistura. Experimentalmente nota-se que se um manômetro for dotado de uma membrana permeável apenas a um dos gases componentes da mistura (i), e se este manômetro for colocado em contato com a mistura, a pressão registrada será igual a p_i ao invés da pressão total p; portanto, a pressão parcial é uma entidade física e não puramente matemática, podendo ser determinada por métodos físicos sem a necessidade da abstração implícita à lei de Dalton.

Para o caso de dois gases 1 e 2, nas condições p, V, T, n₁ e n₂, as equações parciais de estado são:

p₁ = n₁       e       p₂ = n₂                (1-34)

e a equação geral de estado é:

p = (n₁ + n₂)                (1-35)

Dividindo-se as equações (1-34) pela equação (1-35):

p₁/p = n₁/(n₁ + n₂)       e       p₂/p = n₂/(n₁ + n₂)

e lembrando a definição de fração molar, equação (1-7):

p₁ = x₁p       e       p₂ = x₂p

em que x_i é a fração molar do gás i. Se, por exemplo, a pressão parcial do gás 1 for igual a 3 atm e a pressão total da mistura dos gases 1 e 2 for igual a 4 atm, teremos para as frações molares:

x₁ = 3/4 = 0.75       e       x₂ = (p - p₁)/p = 1/4 = 0.25

significando que 75% das moléculas da mistura são do gás 1 e 25% são do gás 2. Decorre da própria definição de fração molar que:

x₁ + x₂ = 1

Generalizando as expressões que relacionam pressão parcial com fração molar para uma mistura de s gases como a da figura 11, temos:

p_i = x_ip                (1-36)

e para a relação entre as frações molares:

x₁ + x₂ + ... + x_s = 1

ou

x_i = 1                (1-37)

O número de variáveis independentes num sistema constituído por s gases é igual a n_C + 2 (vide equação 1-32). Conhecendo-se duas variáveis quantitativas gerais (por exemplo, p e T) e n_C (n_C = s) variáveis quantitativas específicas (m_i ou n_i ou x_i), o sistema estará definido desde que se conheça qualitativamente o mesmo (através do conhecimento dos componentes e, consequentemente, e através de tabelas especializadas, de M_i). Se a variável x_i for a escolhida, deve-se observar que apenas n-1 destas são independentes, a última sendo dada pela equação (1-37); torna-se necessário então, para a resolução da equação, a escolha de mais uma variável, a qual pode ser m ou outra qualquer. O número de variáveis quantitativas independentes num sistema em equilíbrio é chamado variância ou grau de liberdade e para um sistema homogêneo seu valor é igual a n_C + 2.

B-7 REAÇÕES QUÍMICAS ENTRE GASES

Encontramos, no item B-6 a equação geral para uma mistura de gases de composição constante (equação 1-32 ou 1-33). Os i componentes são constantes e o número de moles de cada um também é constante. Logo, a expressão

n_i = n₁ + n₂ + ... + n_s                (1-38)

é constante. Um sistema mais geral é aquele onde ocorrem reações químicas e portanto n_i e/ou i são variáveis e a expressão (1-38) é variável. Se o sistema for aberto (m variável), a generalização estará completa para o estudo dos gases.

	p1      V1      T1 m1i      M1i
			p2      V2      T2 m2i      M2i
	Estado 1		Estado 2
	Figura 12: Transformação geral de estado

A figura 12 mostra uma transformação geral deste tipo na qual um sistema passa de um estado 1 para um estado 2 através de uma ou mais reações químicas e/ou transporte da massa Φ_m do exterior para o mesmo. A equação geral para uma mistura de gases (1-33) pode ser aplicada a cada estado isoladamente:

Estado 1		Estado 2
p1 = n1i		p2 = n2j		(1-39)

em que

n_1i = n₁₁ + n₁₂ + ... + n_1s

e

n_2j = n₂₁ + n₂₂ + ... + n_2r .

Igualando as expressões (1-39) através de R:

                (1-40)

chegamos à expressão (1-40) que é a equação geral para o estudo considerado. Genericamente podemos escrever:

pV = RTn_i                (1-41)

expressão esta que é idêntica à (1-33), porém agora válida para condições em que i e/ou s são variáveis.

A tabela 5 mostra o caráter geral da equação (1-41), notando-se que as equações de estado estudadas até aqui são casos particulares da mesma.

EQUAÇÃO GERAL:		pV = RTni
CASOS PARTICULARES
SISTEMA	VARIÁVEIS	CONSTANTES	EQUAÇÃO DE ESTADO
QUALQUER nc ³ 1	p, V, T e ni	R	pV = RTni
Aberto, sem reações químicas. nc ³ 1	p, V, T e ni	R
Fechado, qualquer nc ³ 1	p, V, T e s	R   e   i
Fechado, sem reações químicas. nc ³ 1	p, V, e T	R,  i  e  s
Aberto, tipo Avogadro nc = 1	V e n e/ou i	p, R e T	ni = AV (i = 1 ou 2 e A = p/RT)
Fechado, qualquer nc = 1	p, V e T	R  e  n ni = n	pV = nRT
Tipo Boyle nc = 1	p e V	T, R e n	pV = B (B = nRT)
Tipo Charles nc = 1	V e T	p, R e n	V = CT (C = nR/p)
Em equilíbrio nc ³ 1	—	p, V, T, R e ni	—
Tabela 5: Equação Geral dos Gases — Casos Particulares

Clique na figura ao lado para continuar a ler o artigo Þ

ou então clique aqui para retornar ao índice deste artigo.
 
 

DHTML Menu By Milonic JavaScript