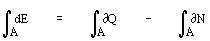Variáveis Escondidas e a Termodinâmica

frames Alberto Mesquita Filho
 Integração I(3):179-81,1995

Este artigo é uma reformulação de Considerações Sobre a Entropia, escrito em setembro de 1984 e não publicado. Trata-se de uma evolução de conceitos expressos em livros do autor (1984 e 1987).

 

Resumo. Uma teoria representacional para a entropia é apresentada, relacionando o aumento da entropia do universo à produção de entropinos (= neutrinos?), e a estabilidade dos sistemas em equilíbrio termodinâmico ao caráter elástico das colisões moleculares em tais condições.

Abstract. A representational approach to entropy: A new approach to entropy is presented, reporting their universe increase to entropin (= neutrin?) productions, and the equilibrium systems stability’s to the elastic character of molecular collisions.

 

1 — INTRODUÇÃO

Dentre as inúmeras maneiras de se enunciar o primeiro princípio da termodinâmica, destaca-se a seguinte:

Se um sistema é sujeito a uma transformação cíclica, o trabalho W produzido nas vizinhanças é igual ao calor Q extraído das vizinhanças, ou seja,

term01          (1)

A igualdade (1) nos induz a caracterizar uma propriedade de estado X cuja diferencial dX é definida por:

term02          (2)

Os tratados de termodinâmica, via de regra, identificam X com E (E de energia), chamando esta propriedade E por energia interna. Os mais precavidos chegam a afirmar que não há nada que nos garanta ser E a mesma propriedade energia definida em mecânica. Com efeito, e conforme afirma Mário Bunge (1974), a termodinâmica é o paradigma da teoria fenomenológica, não se preocupando em descrever fenômenos de calor, mas propriedades muito gerais e leis, com a ajuda de construtos de alto nível tais como energia E e entropia S. Consequentemente, e para ser coerente consigo mesma, ela não deve penetrar em terrenos representacionais. Esta é a característica que a torna uma teoria de baixo risco e um dos fatores que convenceram Einstein a declarar ser a termodinâmica clássica a única teoria física de conteúdo universal que, dentro da estrutura da aplicabilidade dos seus conceitos básicos, jamais será derrubada. O que evidentemente não significa dizer que jamais será explicada.

Ao identificarmos X com E, assumindo ser E a mesma energia estudada em mecânica, evoluímos do fenomenologismo ao representacionismo, evolução que, conforme Bunge (op. cit.), representa o fim último da teorização. A bem da verdade, esta evolução não se dá sem riscos, valendo a pena meditarmos sobre a opinião de Mário Schenberg (1984) a respeito de duas das mais discutidas teorias representacionais que tentaram substituir a termodinâmica:

Há uma coisa sobre a qual a mecânica quântica não lançou luz alguma: o segundo princípio da termodinâmica. Este continua tão misterioso quanto antes. A lei de crescimento da entropia não pode ser até agora deduzida nem pela mecânica estatística clássica, nem pela mecânica estatística quântica. Há, aí, alguma coisa de fundamental que ainda não compreendemos. Quando uma coisa começa a se complicar muito, é sinal de que é preciso simplificá-la.

Um dos temas que polemizou a física dos anos 30 foi o da existência ou não das variáveis escondidas — VE’s — da física quântica. Uma revisão que trata do assunto foi publicada recentemente por Brown (1983), em CiênciaHoje. O questionamento levantado por Einstein, e combatido veementemente por Bohr, até hoje não foi solucionado. A maioria dos físicos optou pelo instrumentalismo de Bohr, fortalecidos que estavam pela demonstração, por Von Newmann, de um teorema a provar matematicamente a inexistência das VE’s. Nem bem Von Newmann publicou seu trabalho, começaram a surgir comprovações experimentais de uma infinidade de VE’s, num número jamais sonhado por Einstein. Merecem destaque o nêutron, o neutrino e a antimatéria.

Epistemologicamente podemos dizer que a inocuidade ou inoperância do teorema de Von Newmann pouco ou nada ajudou o posicionamento de Einstein frente a Bohr. Com efeito, serviu simplesmente para fortalecer a idéia de possuirmos uma ciência aberta, em oposição aos critérios de utilidade defendidos pelos instrumentalistas adeptos de Bohr.

Poucos se deram conta do real motivo do duelo entre Einstein e Bohr. Na realidade, julgava o primeiro que os alicerces em que se apoiava a mecânica quântica estavam condenados, necessitando de reparação urgente. E Bohr, como grande teorizador que era, sabia que, com raríssimas exceções, não se mexe nos princípios de uma teoria representacional, pois que, por menor que seja o remendo, não se consegue evitar a descaracterização total da mesma. Sem dúvida alguma, tanto Einstein quanto Bohr sabiam que nenhuma das VE’s recém-descobertas e tão profusamente comentadas, enriqueciam ou abalavam seus argumentos.

Recentemente (1993 e 1995) defendi a idéia de uma VE de natureza clássica e não tão inócua a esse respeito: a informação eletromagnética. No que se segue, pretendo expor sucintamente uma segunda destas variáveis, a que chamarei por entropino.

2 — AS TRANSFORMAÇÕES NATURAIS

Vamos a princípio admitir que, numa transformação natural qualquer, seja válida a relação:

ΔE = ΔX - ΔN          (3)

em que ΔE representa a variação da energia interna real do sistema, ΔX a variação aparente da energia interna medida por

term03          (4)

e ΔN uma quantidade hipotética de energia perdida pelo sistema sob a forma de entropinos. Os entropinos seriam entidades hipotéticas, talvez partículas, talvez neutrinos, e que, a exemplo destes últimos, não seriam, via de regra, captados pelas moléculas do meio que atravessam. Tudo se passa como se os entropinos fossem absorvidos por um terceiro sistema, alheio aos métodos experimentais rotineiros.

Definidos os parâmetros, resta-nos agora compatibilizar ΔE, ΔX e ΔN com a primeira lei da termodinâmica [equação (1)]. E isto não parece ser difícil.

Consideremos, preliminarmente, um sistema num estado inicial i e tal que possamos levá-lo a um estado final f quer por uma, quer por outra de duas transformações totalmente irreversíveis. Numa delas (A) o sistema apenas recebe calor e perde entropinos, e, portanto,

ΔAE =term04

e na outra (B), ao invés de calor, o sistema recebe trabalho irreversivelmente, ou seja

ΔBE =term05

Como ΔAE = ΔBE, podemos escrever:

term06          (5)

Em se tratando de transformações equivalentes, a primeira lei da termodinâmica nos permite concluir que

term07

Consequentemente:

term08

Ou seja, se N for real, a primeira lei da termodinâmica nos garante que qualquer que seja o processo, desde que totalmente irreversível, ò¶N independe da via, e, portanto, N é uma diferencial exata e N é uma função de estado do sistema. O que é coerente com a equação 3.

Num processo reversível, a identidade n º dN não deve se verificar. Ou seja, para que o universo em estudo retorne à situação primitiva, ò¶N deve ser igual a zero. E, nestas condições, combinando as equações (2), (3) e (4), devemos ter:

ΔE = ò dE = ò (Xrev - Nrev)

            = ò Xrev = ò (Qrev - Wrev).

Ao compararmos um processo reversível e um totalmente irreversível cujo sistema de prova tenha os mesmos estados inicial e final, teremos:

ΔE = ò (Q - W - N)irrev = ò (Q - W)rev          (6)

Se as duas transformações envolverem apenas trocas de calor, como por exemplo a transformação isocórica de um gás, a expressão (6) se simplifica em:

ò (Q - N)irrev = ò Qrev

ou

ò Nirrev = ò (Qirrev - Qrev)

O que não deixa de ser uma conclusão interessante, pois, pelo menos em teoria, permite o cálculo experimental de ΔN. Resta saber se Qirrev e Qrev são significativamente diferentes, ou com diferença passível de comprovação laboratorial, o que, sem dúvida alguma, endossaria o modelo apresentado.

Uma outra comparação interessante é a expansão isotérmica de um gás ideal por vias reversível e irreversível. Neste caso temos:

ΔE = ò (-N)irrev = ò (Qrev - Wrev)

Como Qrev = TΔS e Wrev = ΔA, em que T = temperatura absoluta, S = entropia e A = energia livre de Helmholtz, podemos escrever:

ΔN = ΔA - TΔS (expansão isotérmica)

Quando um gás se expande isotermicamente, ele perde a capacidade de realizar trabalho de um valor igual a ΔA. Sendo o processo reversível, o exterior ganha trabalho, e a variação de entropia externa compensa o aumento de entropia do sistema. Se o processo for irreversível, o exterior aparentemente não se modifica; pelo menos o exterior mensurável. Dizemos, então, que a entropia do sistema, e consequentemente a do Universo, aumenta. Os entropinos, evidentemente, estão fora da conceituação clássica de entropia; isto para não dizermos que estão fora do universo experimental clássico.

3 — DISCUSSÃO E CONCLUSÕES

Acredito que todo processo irreversível, ou seja, todas as transformações naturais — tais como a expansão de um gás, o choque inelástico, as reações químicas, os processos de mistura, etc., — se acompanhem da liberação de entropinos (neutrinos?). Algo, no entanto, resta ser esclarecido: Como um mesmo estado final pode ser obtido por vias tão diferentes? Ou seja, o que um sistema termodinamicamente isolado perde no lugar dos entropinos, quando a transformação sofrida for reversível?

O que caracteriza o processo reversível é a natureza discreta das trocas de calor e/ou trabalho. Estas trocas estão relacionadas a colisões moleculares. Direi, então, que colisões intensas liberam entropinos, sendo portanto irreversíveis. E colisões discretas nada mais são que encontros amigáveis em que uma molécula transfere fótons para a outra; ou, utilizando uma linguagem clássica, a molécula de menor energia cinética capta a energia radiante emitida pela molécula com maior energia cinética.

Processos reversíveis são aqueles em que as colisões moleculares são 100% elásticas. E isto somente ocorre em sistemas em equilíbrio, ou seja, onde o desvio padrão da energia cinética molecular média não ultrapasse um determinado nível crítico.

* * * * *

Debate sobre este artigo na Ciencialist

Referências Bibliográficas:
  • BROWN, H., A. (1983), Estranha Natureza da Realidade Quântica, Ciência Hoje, vol. 2, n.° 7.
  • BUNGE, M. (1974), Teoria e Realidade, Ed. Perspectiva, São Paulo.
  • EINSTEIN, A., Notas Autobiográficas, Ed. Nova Fronteira, R.J.
  • MESQUITA F.° , A. (1984), Os Átomos Também Amam, Editora das Faculdades São Judas Tadeu, São Paulo.
  • SCHENBERG, M. (1984), Pensando a Física, Ed. Brasiliense, São Paulo.

DHTML Menu By Milonic JavaScript