5.1 Fundamental equations:

Two equations among those presented in item 4 are fundamental for the continuation of our analysis. The first is the one that supposedly supplies us the electric effects field produced by an electron (cause-field relationship):

while the other one translates —in terms of force— the electrostatic behavior of an electron place in an electric effects field caused by another or more than one electron (field-effect relationship):

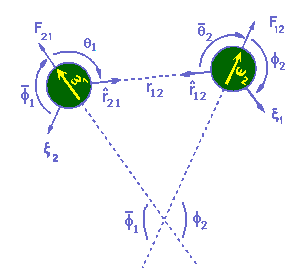
It is important to reaffirm and to point out the complementary meaning between both xs (or vs) of the equations 5.1 and 5.2. In the former, x stands for the field generated by an electron; in the latter, x stands for the field that acts on the electron under consideration. It should also be noticed that we are following the convention adopted in the hypothesis 1: v is the unitary vector, i.e., w = Kv

5.2 The q and f angles:

Let w be a vectorial electron. Moreover, let us suppose that x is the electric effects field produced by the electron under consideration in a P point of a straight r containing the electron. Under these conditions θ is the angle clockwisely measured and starting in w and finishing in r.

Let w be now another vectorial electron. Moreover, let us suppose that w is placed in a x field. Under these conditions f is the angle clockwisely measured and starting in w and finishing in x

Finally let w₁ and w₂ be two vectorial electrons. Figure 10 illustrates through θ₁ and f₂ what was commented in the last two paragraphs. In Figure 10 there we can also find the representation of some conjugated angles (identified by a superior streak). When handling the equations 5.1 or 5.2 it is indifferent to use a certain angle or its conjugated angles because the cosines of conjugated angles are coincident.

Figure 10: Comments in the text

5.3 The internal vectorial product:

We shall define the internal vectorial product of two vectors u, v —denoted by uÄv— to the vector whose module is the same as the internal product (scalar) between both, and whose direction is the one of the second vector (v in this case). We then have

in which it might be noticed that uÄv ¹ vÄu.

Comparing 5.2 and 5.3 and observing the definition for f presented in item 5.2, we conclude that

5.4 The translational of an A vector

The study of field mathematics is made easy by the use of a group of vectorial differential operators such as gradient, divergence and rotational.

The rotational concept is closely connected with the classic concept of vectorial product:

u × A Û Ñ × A .

In this relationship some characteristics stand out as being common to both products; for example, the resulting vector is perpendicular to A in all of the points of the domain of A. However, in the first case (vectorial product) the resulting vector u×A has a direction depending exclusively on the directions of u and A in the considered point and is independent from the value of A in other neighboring points; and this direction is due to physical-mathematical conveniences (by definition) perpendicular to both u and A. But in the second case (rotational) they enhance the following important properties:

1. Ñ is a differential operator which —regardless of some of its mathematical characteristics which identify it in algebraical terms to a vector— is not a vector and, therefore, does not present a defined direction;
2. after defining Ñ and knowing the A field, we are not able to choose a direction for Ñ´A;
3. the Ñ´A direction depends on the behavior of A in the vicinity of the considered point;
4. the existence of Ñ´A as a vectorial field is not intuitive: it is backed by the obedience to rigid physical-mathematical rules [35] [36];
5. because Ñ´ is a differential operator it operates in order to satisfy the partial differentiation rules including the differentiation of a product.

In general the rotational of a field is related to the rotation properties of the field [37]: its value can be grossly calculated by the observation of the circulation around a small area element. It is a kind of collateral derivation involving the variation rate of A_x according to y or z [38].

We will now try to expand these ideal to the concept of internal vectorial product.

In the first place it should be noticed that —out of convenience— we chose a direction for the internal vectorial product, uÄA, which coincides with the direction of A in such a way that

uÄA = (u.A) Â

In this case, unlike the classic concept of vectorial product, the direction of the resulting vector is independent from the direction of vector u. If we want to find a differential operator promoting an internal vectorial differentiation in an A field so that we can find a relationship such as

uÄA Û ÑÄA,

the resulting vector should have a direction independent from the Ñ differentiation such as

The internal vectorial product of Ñ for A —ÑÄA defined according to 5.5— will be called translational of A. This denomination is justified because the translational of a vectorial field in some important cases reminds the directional derivative of this field according to the field lines.

	Contents
Return		Advance