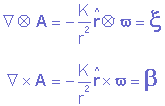6.1 The A field

How does an elementary particle read a field, thus reacting to its implicit content? Let us think of a force field that be electric, magnetic or gravitational. These are effect fields, i.e., areas of space endowed with some particularities and producing measurable effects on certain test objects. Therefore it exists a local and specific potential which is provoked by a physical property continually varying from point to point. Any particle of finite dimensions —so long as it is sensitive to this local property— reacts to this field; in a similar way to a macroscopic object when submitted to a windstorm.

An electric field x can be thought of as a specific derivative of another vectorial field A, since A mathematically comprehends this function. So let us suppose that this A field does exist and possesses —on every point of its domain— all the directional derivatives and is consequently endowed with regular field lines. For example, in order to satisfy hypothesis 4 (H-4), we had to imagine what the A field of an electron should be:

in which represents the derivative according to the field lines of A in relationship to the arch length l or —simply— the curvilinear derivative according to the l field lines of A in the considered point. It then elapses from equation 5.1 that

and this equation —according to the Cartesian reference model (v // k)— changes into

Consequently, A_x = C₁ and A_y = C₂ —with C₁ and C₂ constant. If we recall that A represents the local content of electromagnetic information in transit —emitted by the electron (H-2 and H-3)— we must have

and, therefore, C₁ = C₂ = 0. Under these conditions l coincides with the z axis and the expression for A_z has as a solution A_z = K/r + C₃ which for similar reasons to what was discussed above (for C₁ and C₂) has C₃ = 0. The solution for 6.2 will be —with w defined in H-1:

agreeing with H-3 and —as we shall see below— with H-4; therefore, it is the electron at rest equation.

Now calculating the translational and the rotational of A with its value defined by 6.3 we easily get to the expressions:

in which b (in 6.4) satisfies Biot-Savart’s law; therefore, it is the magnetic effect field of an electron at rest —and A totally satisfies the basic hypotheses.

It is interesting to notice that we began our arguments using Coulomb’s law for a sphere with an infinite radius, and we arrived at Biot-Savart’s law; it is more interesting to verify the mathematical reversibility of theoretical path: it is possible to leave from Biot-Savart’s law and arrive at Coulomb’s law. In fact, these laws are mathematically equivalent and equations 6.3 and 6.4 operate the transformation from one into another.

6.2 The fundamental equations of the electromagnetostatics

The field of electromagnetic effects of an electron at rest is summarized by the following system of equations

with A given by 6.3. Since fields x and b are addictive (Superposition Principle) but the translational, unlike the rotational, does not obey the distributive property, system 6.5 is not to be generalized to all electromagnetic fields. In other words, the electromagnetic field (x,b) of a population of electrons cannot as a rule be expressed in terms of a single A vector [This fact answers for the unyielding character of Maxwell’s equations]. In this case then have

The corresponding effect equation is

with x and b calculated by 6.6; F_j is the electromagnetic force that acts upon an electron j placed in an electromagnetic stationary field; K₁ and K₂ are constant. Equations 6.5 and 6.6 keep in their contents the totality of the electromagnetostatics (with the exception of an important factor related to the induction field t mentioned in item 3.3).

6.3 The scalar electromagnetic field

It is possible [39] to consider the electromagnetic field of an electron through a scalar function φ given for

Therefore, it is enough to define x and b through the expressions

and to observe that the function φ presents the following properties

So, we can easily demonstrate that

and consequently the compatibility between 6.8 and 6.3.

6.4 The electromagnetic information (e.m.i.)

Equations 6.9 show us that the electromagnetic field (x,b) of the electron can be described in terms of the gradient of a function position φ. So, we may conjecture about the actual existence of something emitted by the electron and call it electromagnetic information (e.m.i.). Equation 6.8 suggests something else —once emitted the e.m.i. are preserved. In other words the electron is an e.m.i. emitter source and the e.m.i. flow that crosses any surface identifies itself with the flow of an h vectorial field expressed by

It is implicit in these considerations that h belongs to the h = ρc type, when ρ is an invariant that represents the local density of e.m.i. and c is the speed spread by these e.m.i. in an appropriate reference system.

	Contents
Return		Advance