7.1 The inertial systems

When a Coulomb’s electric charge passes from a resting state to another in a rectilinear and uniform movement, it emits an aura and defines two universes during this acceleration phase:

Figure 11: Electric field of a charge in movement

1. an inner universe containing the charge field adapted to its inertial movement — here everything happens as if the charge were at rest in a reference frame that travels with the charge in a uniform movement;
2. an other external universe that contains the charge field at rest in the initial inertial reference frame.

The aura consists of a mobile membrane of finite thickness and it is the headquarters of a mutant field named electromagnetic radiation. When this aura crosses an area of the space in a considered speed it promotes the transformation of the inertial field (the one with the charge at rest) into another (the one with the charge at rectilinear and uniform movement).

This phenomenon also happens to electrons since they are accelerated into specific directions as, for example, into an electric current, or enter the plates of a capacitor, or when deviating the direction to the nucleus of an atom while moving from an orbit to another.

How could the electron field be in a non-inertial system of reference? How could the electron equation be under these circumstances?

We have seen the 6.3 equation of the electron at rest in the reference system in which we lived. The founded function does not present any dependence on time. We should suspect, however, that the equation of the electron at rest in an accelerated reference system shows some dependence on time. And we should also admit that in an allowed orbit the electron equation —obtained from a reference frame that followed it in this movement—should present a solution that is different from 6.3 in a periodic way and presents a stationary character.

The equations presented in the previous items were deduced in a very special reference system —in the reference frame of Coulomb’s laboratory— or, still, in the reference frame in which Newton deduced the laws of mechanics. What should be made to generalize them? What is an inertial reference system?

The success of classic mechanics is more than enough to guarantee the existence of the inertial system. In spite of this, classic mechanics did not succeed in defining an inertial reference frame. Quoting Einstein and Infeld: classic mechanics floats in the air because we did not find any rule to determine an inertial system [40].

By the end of the last century physicists tried to define inertial systems in such a way that they could be adjusted to classic mechanics. They adopted the logic of trying to consider them under field theories like Maxwell’s. So they tried to characterize a Maxwellian inertial frame of reference which, however, was incompatible with the Newtonian inertial reference systems [41]. Einstein’s relativistic physics raised from this incompatibility.

In this article, we are trying to interpret electromagnetism in a different way from the commonly adopted one —it is time to try to abolish this incompatibility. So I shall say that

7.2 Appropriate and non-appropriate reference frames

I shall say that an appropriate reference frame is the one in which the electron being studied keeps P and w constantes. constant. It is, therefore, the reference frame adapted for the mathematical analysis of the electromagnetic field of the electron because this field is the function of w and r. Particularly if the appropriate reference frame is inertial, the electromagnetic field of the electron will simply be the functions of these two variables (equations 6.5). In the rest of this article we will only study fields produced by electrons placed in an appropriate and inertial reference frame.

7.2.1 The observer placed in a non-appropriate reference frame

The x and b fields —when observed through a non-appropriate reference frame— manifest an effect that is linked to a phenomenon described by Liénard (1898) and Wiechert (1900) for the potentials of Maxwell’s theory. This phenomenon should be carefully analyzed because x and b are functions of two variables (φ and w). Both contributions are interesting but the one that owed w acquires epistemological importance because it generates fateful consequences for the classic physics [42]. The non-consideration of this portion evidenced the foundations upon which Einstein’s relativity theory was established.

In the first place let us see how φ is transformed. With the considerations made in item 6.4, expressed by equation 6.11, we can admit that when ρ is an invariant, h (and consequently φ) is transformed according to:

h = ρc  Û      h' = ρc' ,

in which c' = c + v, when v is the speed of the e.m.i. emitter electron and observed from the non-appropriate reference frame.

Now let us see how w is transformed. Then, let us consider an observer placed in a Q point of an inertial reference frame and an electron placed in a P point and moving in relationship to this inertial system with a constant speed v. So I will say that the v unitary vector appears for the observer in Q as if it were another unitary vector, v’, which suffered an aberration preserving its unitary module. For the calculation of this aberration and observing the conventions adopted in figure 11 we should do the following:

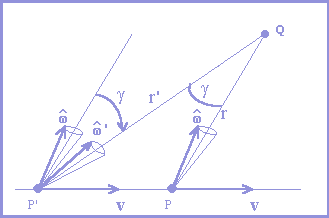	Figure 12: Aberration of v (v Þ v'). P = position of the electron in an instant t in relation to a non-appropriate inertial reference frame — where the electron travels in a v constant speed, keeping v constant and in which the observer is at rest in Q. P' = position of the electron in a t' delayed instant in which the field that arrives in Q in t instant was generated.

1. to determine the P’ point admitting that the field spreads in a radial way with a c speed when analyzed from the appropriate reference frame;
2. to join the points P, P’ and Q;
3. to trace a cone with the vertex in P and containing v in its surface, with the axis in the PQ direction;
4. to transfer the cone with v to P’;
5. to rotate the cone around P’ and according to a perpendicular axis to the plan of the figure (plane PP’Q) until the axis of the cone is located in the P’Q direction;
6. the unitary vector obtained by this rotation of v it is v’.

As I observed in a previous article [40], the K scalar of hypothesis 1 (and, therefore, the absolute value of vector w), seems to contain some secrets related to the inertial reference frame that only experimental physics can decipher. It would be extremely interesting to verify whether its absolute value, once defined, keeps or not an identical whatever reference inertial frame is considered. The K variability, as I believe, would be a strongly suggestive indication to corroborate Newton’s intuition in relationship to the existence of an absolute reference system. It can be expected, however, that K keeps constant for v < < c.

7.3 The (x,b) field of the electron in movement

When the transformations for h and v are known, we can despise the apostrophes and assume that the x and b fields are expressed by

both in the appropriate reference system and in the non-appropriate reference system. It elapses then from 7.1. —regardless of the considered inertial frame of reference —the sum x² + b² is a classic relativistic function of position:

h² = x² + b²

	Contents
Return		Advance

DHTML Menu By Milonic JavaScript