O fenômeno luz e as falácias relativas às relatividades

logoAlberto Mesquita Filho
01/06/2000
 
 
 Página 1


  1. Colocação do Problema
  2. Interpretações Clássicas e Relativistas
  3. Relatividade e Senso Comum
  4. A Experiência de Michelson-Morley
  5. A Transformação Massa-Energia
  6. A Dilatação do Tempo
  7. Eletromagnetismo e Sistemas Inerciais
  8. Outras Aparentes Inconsistências Clássicas
     

Obs.: As expressões relativista e relativístico(a) serão utilizadas neste artigo a caracterizarem significados relacionados a fenômenos ou efeitos que, na visão dos físicos modernos, seriam explicados somente pela teoria da relatividade de Einstein.

1 Colocação do Problema

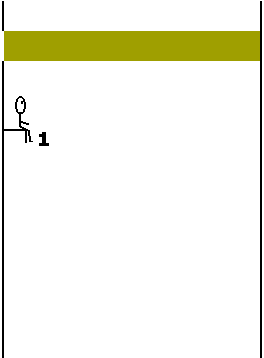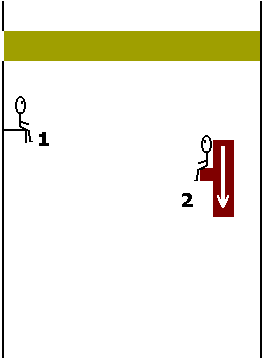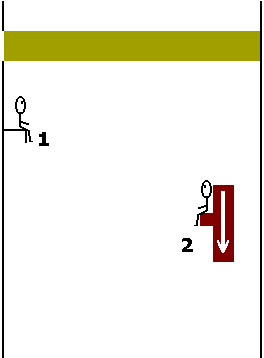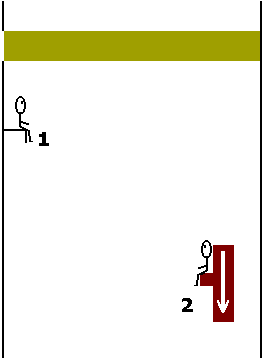
Imagine um trem em movimento na velocidade v, da ordem de c (a velocidade da luz no vácuo), ou seja, numa velocidade na qual não podemos desprezar os chamados "efeitos relativísticos". No interior desse trem temos dois observadores: um observador (1) fixo ao trem e o outro (2) fixo a uma plataforma que se move em direção à traseira do trem com o mesmo módulo da velocidade v do trem. Nestas condições podemos dizer que (2) está em repouso em relação à terra firme, ainda que situado no interior do trem.

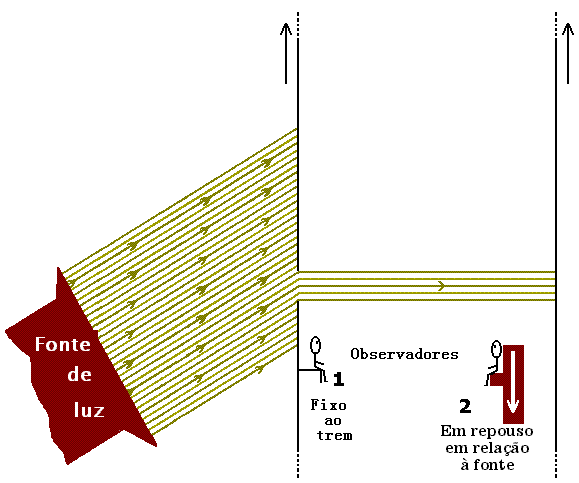
O trem está dotado de um orifício e a luz, vinda de uma fonte em repouso, penetra por este orifício sem sofrer difração apreciável (o orifício é grande o suficiente para que a difração não ocorra). A fonte emite feixes paralelos de luz numa direção tal que os feixes de luz atravessam o vagão transversalmente, de um lado a outro e, portanto, na direção perpendicular à da velocidade v. A figura 1 ilustra o comentado.

trem01

Figura 1: Explicação no texto. Clique na figura para ampliar.

Vamos ainda supor que os observadores (1) e (2) apenas observam o feixe de luz, sem saber o que está acontecendo no meio exterior ao trem. Para o observador (1) tudo se passa como se o trem estivesse em repouso; e para o observador (2) todo o interior do trem está em movimento, exceto a plataforma que sustenta sua poltrona. Para ambos, a fonte de luz pode ser encarada como sendo o orifício por onde a luz penetra no trem. Esta suposta fonte estaria em repouso para o observador (1) e em movimento para o observador (2). Eles não tem conhecimento sobre o que se passa com a verdadeira fonte emissora de luz, aquela apresentada na figura 1.

Seria possível a luz viajar na direção assinalada na figura 1? A figura 2 é um gif-animado construído com a pretensão de explicar como isso seria possível. Os feixes originais são praticamente "cortados" pelo orifício e a somatória das frações que realmente atravessam o orifício mostra-se, para os observadores situados do lado interno do trem, como um novo feixe, dirigido na direção transversal. Um dos "raios" de luz está colorido em vermelho para realçar esse efeito. Não há como, pela análise macroscópica deste "feixe", avaliar o efeito desses "cortes" sobre a natureza da luz. Tudo se passa, do ponto de vista macroscópico, como se a fonte estivesse realmente acompanhando o trem em seu movimento.

anitrem02
Figura 2: Explicação no texto.
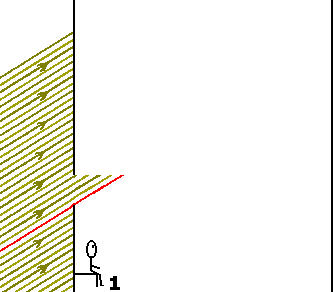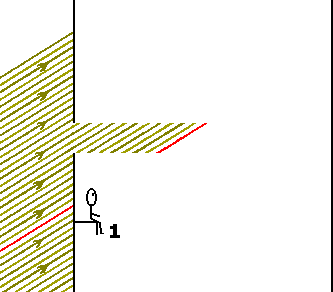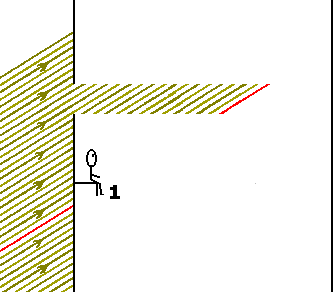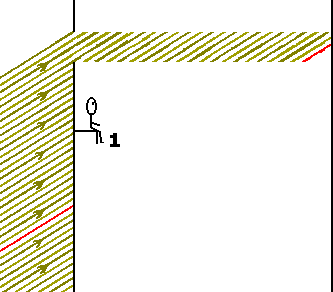
Clique em "Parar" em seu browser para obter imagens congeladas. A seguir clique em "Atualizar"

Os observadores poderiam estimar a trajetória do feixe de luz sob duas condições: 1) admitindo uma propagação retilínea entre o orifício de entrada e a imagem observada no anteparo, ou seja, na face lateral oposta do trem; 2) através de uma cortina de fumaça. As figuras 3 e 4 (gifs animados) mostram como seriam observados os feixes de luz segundo admitia-se, classicamente, ao final do século XIX, antes do advento da teoria relatividade especial.

anitrem03   anitrem04
Figura 3: Visão do Observador 1 segundo a física aceita ao final do século XIX.   Figura 4: Visão do Observador 2 segundo a física aceita ao final do século XIX.

A interpretação clássica, como aceita ao final do século XIX, aparentemente não chegou a ser muito alterada com a teoria da relatividade especial de Einstein. Segundo esta, objetos que se movem em velocidades relativísticas apresentariam, para um observador em repouso, modificações longitudinais no sentido do movimento. Desta forma, o observador (1) veria o feixe exatamente como apresentado e o observador (2) notaria apenas uma diminuição na espessura do feixe (contração no sentido do movimento do orifício e do feixe como um todo).
 

2 Interpretações Clássicas e Relativistas

2. 1 Uma visão clássica ingênua

O observador [1] (figura 3) ao supor que a fonte de luz está em repouso, e sem saber que o trem move-se em velocidade relativista, poderia concluir, com base nos conhecimentos da física clássica vigentes no final do século XIX, que a velocidade da luz observada é x1 = c (velocidade da luz no vácuo). O observador [2], por outro lado, admitindo-se que realmente enxergue a luz como mostrado na figura 4, concordará que a fonte de luz está em repouso em relação ao trem e, portanto, que a velocidade observada por [1] é realmente c. Acreditará, no entanto, que, em seu referencial, qualquer "elemento infinitesimal de volume" do feixe estará viajando na diagonal em uma velocidade x2 maior em módulo do que c (figura 5). E o feixe, qual um bloco maciço, estará viajando na velocidade v, na direção da frente do trem.

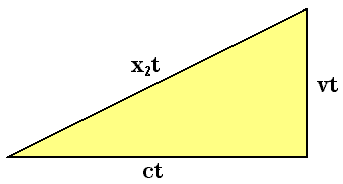
trem05            eq01

Figura 5: Cálculo da velocidade x2

2.2 Uma visão clássica não ingênua

Se o observador [1] se der conta de que não sabe realmente se a fonte de luz está ou não em repouso em relação ao orifício, por onde a luz penetra no trem, perceberá que, com seus conhecimentos de física clássica, e sem equipamentos adequados, não poderá concluir nada a respeito da velocidade da luz que observa, a menos que saiba qual é a real velocidade da fonte, quando observada de seu referencial. Se dissermos a ele que o trem viaja a uma velocidade v em relação à fonte de luz, poderá então estimar graficamente a velocidade da luz em seu referencial, chegando a um valor x1 menor em módulo do que c (figura 6). O observador [2], também cientificado deste fato, perceberá agora que a fonte de luz está em repouso no seu referencial. Logo calculará diretamente x2 = c sem precisar apelar para gráficos, pois a luz, em seu referencial, não viaja na direção transversal ao trem (direção do feixe), o que ele estava admitindo anteriormente.

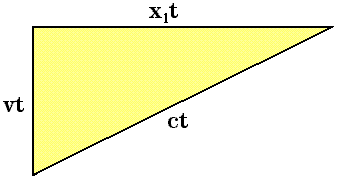
trem06            eq02

Figura 6: Cálculo da velocidade x1

2.3 Uma visão clássica um pouco mais sofisticada

Sem contrariar o assumido no item 2.2, poderíamos fazer algumas correções a respeito de qual seria realmente a visão do observador [2] com respeito ao feixe de luz. A imagem que ele tem do feixe relaciona-se a objetos em repouso no referencial do trem, tais como o orifício, a imagem no anteparo e as partículas de poeira ou fumaça, a propiciarem a visão integral do feixe. Ainda que a fonte de luz esteja em repouso no seu referencial, o feixe em si mostra-se a ele como um cilindro maciço a mover-se com o trem. Se assumirmos uma visão estritamente newtoniana, e não meramente "clássica", concluiremos que, pelo fato de [2] estar em movimento em velocidades relativistas em relação a esse cilindro, ele NÃO enxergará um feixe retilíneo mas ligeiramente curvo, num formato a lembrar uma hipérbole; e tanto mais distante da reta quanto maior for o valor de v (este detalhe é discutido com mais detalhes em "O Espaço Curvo Euclidiano e a Relatividade Galileana)". Isto não deverá afetar seus cálculos pois trata-se de uma ilusão de óptica provocada por uma aberração de natureza relativista. O efeito poderá, no entanto, orientá-lo no sentido de mostrar-lhe que o "feixe curvo" que efetivamente enxerga, não existe como tal no espaço, a menos que considerado como uma imagem a retratar agrupamento de pontos que jamais existiram como eventos simultâneos.

2.4 Os postulados da relatividade especial

De acordo com a teoria da relatividade especial (1, 2), a velocidade da luz é a mesma em todos os sistemas coordenados que se movem uniformemente uns em relação aos outros (postulado 1); e as leis da natureza são as mesmas nestes referenciais (postulado 2). A teoria da relatividade geral (3) engloba esses dois enunciados como casos particulares de um enunciado mais geral (princípio da relatividade geral) a contemplar também referenciais acelerados. Digna de nota, é a independência da velocidade da luz em relação à fonte e, consequentemente, em relação ao referencial no qual a fonte de luz está em repouso. A relatividade especial justifica-se na teoria eletromagnética de Maxwell-Lorentz e na incompatibilidade desta última com a mecânica clássica conforme era aceita no final do século passado, e não propriamente e/ou diretamente, no fenômeno luz em si; tanto é que o primeiro artigo a respeito chama-se "Sobre a eletrodinâmica dos corpos em movimento" (1). O argumento a convencer Einstein a caminhar da relatividade especial para a geral, relaciona-se a experiências de pensamento, destacando-se aquelas relativas ao que foi chamado "Elevador de Einstein", importantes para que chegasse a formular o seu princípio da equivalência (4).

Consoante o postulado 1 de Einstein devemos ter então x1 = x2 = c. As aberrações comumente descritas nos casos mais simples, em que procura-se aplicar a relatividade especial, e a contrariarem o senso comum, ganham novas proporções ao analisarmos casos como este apresentado em que as mudanças de referencial processam-se em direções diferentes à da propagação da luz considerada. Para que se tenha uma idéia veremos, a seguir, como o observador [1] poderia ingenuamente imaginar a mudança de referencial.

2.5 Uma visão relativista ingênua

Para o observador [1], um "elemento de volume" do feixe de luz que acabou de passar pelo orifício (poderia ser um fóton), atravessará toda a largura do trem, ou o segmento AB mostrado na figura 7, no intervalo de tempo t1. Sabendo que para o observador [2] o trem move-se numa velocidade v, ele concluirá que, na visão deste observador [2], quando o "elemento de volume" passou pelo orifício, o orifício ocupava uma posição A', diversa daquela que deverá estar ocupando após t1, qual seja, A. Sendo v a velocidade do trem, calculará o segmento A'A = vt1. E sendo c a velocidade da luz, assumirá como válida a expressão AB = ct1. Perceberá então que no intervalo de tempo t1 não seria possível, pela relatividade especial, o "elemento de volume" considerado percorrer o segmento A'B na velocidade c pois que para tal deveria possuir uma velocidade x2 > c (figura 7).

trem07            x2 > c

Figura 7: Explicação no texto

Estando corretos os demais pressupostos, [1] chegará à conclusão de que quando o "elemento de volume" atingiu o ponto B em seu referencial, muito provavelmente, na visão do observador [2], o "elemento" ainda estará percorrendo o segmento A'B na velocidade c, sem ter atingido B. Conclui então que os dois eventos (entrada do "elemento de volume" no trem e chegada na parede oposta) não podem ser simultâneos nos dois referenciais, o que está de acordo com o previsto pela teoria da relatividade especial. Ao tornarmos um dos eventos coincidentes (passagem do "elemento de volume" pelo orifício), o outro ocorrerá de maneira a caracterizar a não simultaneidade. Esta não simultaneidade, ao contrário daquela apontada no item 2.3, não seria um efeito ilusório mas real e a denotar a chamada "dilatação do tempo". Um dado interessante e peculiar a esse modelo é que adotando-se os postulados da relatividade especial, tanto o observador [1] quanto o [2] concluirão que a "dilatação do tempo" afetará tão somente o relógio do observador [2]. Chega-se facilmente a essa conclusão construindo-se a figura correspondente a como [2] iria interpretar a constância de c, segundo seu ponto de vista. Com efeito, esta visão "ingênua" leva-nos a uma nova versão do paradoxo dos relógios (ou dos gêmeos) a denunciar uma inconsistência: ou no raciocínio utilizado, ou na teoria da relatividade especial.

2.6 Uma visão relativista não ingênua

Sabemos, pela teoria da relatividade especial, que a luz não pode ser pensada como um objeto comum. Tanto é que a velocidade c de seus componentes, sejam eles fótons, sejam elementos de volume, "não pode" (postulado 1) ser somada à velocidade v de um hipotético observador a caminhar paralelamente ao feixe de luz. Ora, no item anterior estávamos considerando a modificação na direção da velocidade c como seria vista por um observador [2], decorrente de seu movimento numa direção perpendicular a c; ou seja, estávamos admitindo como certa uma das características implícitas à soma vetorial de velocidades (c + v). Mas se "a velocidade da luz in vacuo é a mesma em todos os sistemas coordenados que se movem uniformemente uns em relação aos outros", não deveríamos também considerar a manutenção de sua direção? Não é comum observarmos este efeito em textos de relatividade especial, onde são considerados apenas efeitos unidimensionais e com luz e observador movendo-se na mesma direção; porém não deixa de ser esta a característica "contrária ao senso comum" e a se manifestar quando c e v têm direções não coincidentes.

Mas em que este efeito contraria o senso comum? Muito simples. O observador [2] observa realmente o feixe de luz como um objeto sólido disposto transversalmente em relação ao trem e viajando no sentido longitudinal, como mostrado na figura 4; no entanto, ao pensar em um dos fótons desse feixe, o observador [2] "não pode" dizer que os fótons caminham num sentido não transversal A'B, como mostrado na figura 8 abaixo. Os fótons viajam na velocidade c no sentido longitudinal do feixe e "não existe nada concreto", e a ser aceito pela teoria da relatividade especial, a viajar na direção A'B. Percebe-se, desta maneira, como a teoria da relatividade especial contraria o senso comum, quando estudada em duas dimensões espaciais. Se pensássemos num elemento de volume de um fluido, por exemplo água, a caminhar por um cano ôco, haveria uma soma de velocidades vetoriais e este elemento de volume estaria realmente viajando segundo a trajetória A'B.

trem08         c = c (identidade vetorial)
Figura 8: Explicação no texto

Através desse raciocínio incomum, resolve-se o paradoxo apontado no item anterior. A não simultaneidade decorre graças à mesma dilatação temporal observada ao compararmos eventos registrados em referenciais que se movem na direção do movimento do trem. Cada um dos observadores assumirá a dilatação temporal como sendo um efeito relativístico a ocorrer no referencial do outro observador e que, segundo a sua visão de repouso, é quem efetivamente está em movimento.

Esta idéia de "constância vetorial absoluta" da velocidade da luz c certamente era aceita por Einstein. Tanto é que, em meio a suas experiências de pensamento em duas dimensões, ao evoluir da relatividade especial para a relatividade geral, teria afirmado (5): "Vê-se também que o princípio da constância da velocidade da luz no vazio tem de ser modificado"; modificação esta que ficou implícita no princípio da relatividade geral (curvatura da trajetória da luz devida à aceleração, mas não à velocidade).

Se pensarmos, no entanto, na fonte real de luz, como apresentada na figura 1, a teoria da relatividade fica a nos dever algumas explicações: Como um fóton, lançado inicialmente numa direção A'B pode, pelo simples fato de ultrapassar um orifício, "ficar proibido" de viajar nesta mesma direção? Estaria a teoria da relatividade interpretando ao "pé da letra" a identidade "orifício-fonte de luz" assumida pelas teorias ondulatórias? Mas neste caso a difração foi assumida como desprezível! Por outro lado, o que realmente é um fóton? E o que realmente é uma fonte de luz?
 

3 Relatividade e Senso Comum

3.1 Senso comum e obviedade

Nem tudo o que é óbvio é certo mas tudo o que é certo parece-nos sempre ter um lado óbvio. Senso comum, como rotineiramente a expressão é utilizada, refere-se a explicações aparentemente óbvias para o leigo no assunto e nem sempre a corresponderem à realidade descrita pelo especialista. Ao dizermos que o Sol gira em torno da Terra com um período de 24 horas, estamos dizendo uma verdade a apoiar-se no nosso senso comum. O astrônomo, no entanto, tem argumentos outros a convencerem-no de que é a Terra quem está a girar sobre si mesma e a dar-nos esta falsa impressão.

Assim como a física clássica do século XVII desenvolveu-se graças à procura por uma verdade apoiada na experimentação, e não apenas no senso comum, os precursores da física moderna procuraram, por meios não óbvios, explicar certos fenômenos observados no final do século XIX e, "aparentemente", a falsear a física clássica. Realmente, falseavam! Não a física clássica em si mas o que poderíamos chamar "a física do final do século XIX".

Os métodos utilizados pelos físicos modernos, e a contrariarem o senso comum, diferem significativamente daqueles utilizados pelos físicos clássicos. Para um físico genuinamente clássico, não importa de que século seja, observar algo que contrarie o senso comum implica num convite à procura por uma nova explicação, também óbvia, e a caracterizar um progresso no entendimento dos fenômenos naturais. Encontrada a nova explicação, o senso comum se restabelece, posto que observamos agora o fenômeno sobre um novo prisma, como é o caso do giro da Terra sobre si mesma. Para um físico moderno, observar algo que contrarie o senso comum implica no convite à procura por uma justificativa a se adequar a seus experimentos mas nem sempre à razão. Se existir um lado óbvio, ótimo! Se não existir, fabrica-se um novo senso, através de um consenso comum, a contrariar não apenas o senso comum do leigo mas até mesmo aquele do especialista no assunto. E é este o sentido de "senso comum" que um físico moderno procura dar quando afirma que o que distingue a física moderna da física clássica é o fato da primeira ser contrária ao que denomina "senso comum".

Às vezes o consenso comum, por força de vício, "ganha" a condição de "senso comum", ou seja, acostumamo-nos a nos enganarmos. Cria-se então o que poderíamos chamar por "novóbvio", ou seja, "algo aceito como óbvio por falta de coisa melhor". É desta forma que aceita-se hoje como óbvia a constância absoluta da velocidade da luz, a desrespeitar até mesmo as mudanças de referencial. Apenas os jovens, ou calouros no assunto, são os que sofrem durante um curto intervalo de tempo, com a sensação da falta de alicerces sólidos a sustentarem uma infinidade de conhecimentos a se apoiarem neste vazio epistemológico. À medida em que o "novo senso comum" é fabricado, não é raro observar-se a pretensão de alguns a justificarem o surgimento do que consideram uma "nova física clássica". É nesse contexto que alguns tratados de física quântica chegam a afirmar que a teoria da relatividade de Einstein é uma teoria clássica. Estão com isso meramente querendo enfatizar que a teoria da relatividade de Einstein não se encaixa entre aquelas que, por serem não-locais, contrariam o senso comum a incorporar o princípio da indeterminação de Heisenberg; como que, pretensamente, querendo dizer que física clássica é apenas aquela que ignora este princípio, pois os demais princípios da física moderna seriam por demais "novóbvios".

3.2 Porque aceitar a relatividade de Einstein se ela vai contra o senso comum?

Se, por um lado, a teoria da relatividade de Einstein ainda não justificou sua razão de ser, pois não conseguiu mostrar seu lado óbvio, por outro, como afirmam, apoia-se na experimentação e explica fenômenos que, supostamente, não são explicados por nenhuma teoria física clássica. A esse respeito, nunca é demais afirmar que Einstein, praticamente sozinho, e durante mais de trinta anos, tentou sem sucesso justificar a razão de ser de sua teoria. Jamais ignorou que sua teoria era, como efetivamente é, uma teoria incompleta. E por ser incompleta, fica a nos dever inúmeras explicações, por mais que explique o que seria supostamente inexplicável por outras vias.

Dentre as miraculosas explicações da teoria da relatividade de Einstein enfatiza-se as seguintes (tomei esta relação de empréstimo de um diálogo amistoso que mantive na ciencialist, lista de discussão sobre ciência, e que pode ser encontrado na mensagem 4651, tendo sido acrescentado apenas o item 6 — o diálogo começa na mensagem 4553):

  1. O fracasso da experiência de Michelson-Morley;
  2. A transformação entre massa e energia;
  3. A dilatação do tempo observada no decaimento de partículas elementares velozes;
  4. As leis do eletromagnetismo são as mesmas em todo sistema inercial;
  5. A precessão do periélio da órbita de Mercúrio;
  6. Deflexão da luz por um campo gravitacional;
  7. Parte da estrutura fina nos espectros atômicos.

Em outras palavras: A teoria da relatividade moderna é aceita não porque tenha firmado sua consistência mas porque não encontrou-se, até o momento, nada que explicasse, sem ferir o senso comum, aquilo que apenas ela tem sido capaz de explicar. Percebe-se então que de nada adianta retratarmos possíveis falácias relativas às relatividades se não conseguirmos demonstrar que uma física a se apoiar no senso comum, qual seja, uma física clássica genuinamente newtoniana, possa explicar o que pretensamente somente seria explicável com argumentos "fabricados" pela física moderna.

avançar

Clique na figura ao lado para continuar a ler o artigo Þ

ou então clique aqui para retornar ao índice deste artigo.
 
 

Postulados:

  • Postulado 1 de Einstein: A velocidade da luz in vacuo é a mesma em todos os sistemas coordenados que se movem uniformemente uns em relação aos outros.
  • Postulado 2 de Einstein: Todas as leis da natureza são as mesmas em todos os sistemas coordenados que se movem uniformemente uns em relação aos outros.
  • Princípio da Relatividade Geral: As leis da natureza são as mesmas, quaisquer que sejam os sistemas coordenados gaussianos (Vide Gaussian Co-ordinates) em que sejam formuladas.
  • Princípio da Equivalência de Einstein: É impossível descobrir, por experimento, se um dado sistema de coordenadas é acelerado, ou se seu movimento é retilíneo e uniforme e os efeitos observados são devidos a um campo gravitacional.

Referências:

  1. EINSTEIN, A.: Sobre a Electrodinâmica dos Corpos em Movimento, 1905, em Textos Fundamentais da Física Moderna, vol.1, O Princípio da Relatividade, Fund. Calouste Gulbenkian, Lisboa, 1958. On the electrodynamics of moving bodies.
  2. EINSTEIN, A.; L. INFELD.: A Evolução da Física, Zahar Edit., Rio de Janeiro, 1980.
  3. EINSTEIN, A.: Relativity, the Special and General Theory (1916), Bonanza Books, New York, 1961.
  4. EINSTEIN, A.: Pensamento Político e Últimas Conclusões, Ed. Brasiliense, São Paulo, 1983.
  5. EINSTEIN, A.: Os Fundamentos da Teoria da Relatividade Geral, 1916, em Textos Fundamentais da Física Moderna, vol.1, O Princípio da Relatividade, Fund. Calouste Gulbenkian, Lisboa, 1958.

DHTML Menu By Milonic JavaScript