A NATUREZA DA LUZ E PRINCÍPIO DA SUPERPOSIÇÃO
Capítulos VII e VIII
VII.1 - A Polarização como tema crucial
A polarização representa sempre um tema de importância crucial para todos aqueles que sonham decifrar segredos relacionados à natureza luz. Para Newton, a polarização foi um dado importante a convencê-lo de que luz seria um fenômeno corpuscular. Para Fresnel, a polarização constituiu-se num impecilho, a complicar terrivelmente suas tentativas em caracterizar a luz como um fenômeno exclusivamente mecânico ondulatório. Para Faraday, o relacionamento entre a polarização da luz e o campo magnético representou um trunfo, a demonstrar-nos ter sido tanto mais importante quanto mais nos lembrarmos de que foi esse o fenômeno a convencer Maxwell de que a luz era um fenômeno ondulatório eletromagnético. Hoje a polarização da luz constitui-se no mais importante alicerce a sustentar o mais fundamental dentre todos os princípios da mecânica quântica: o princípio da superposição de estados.
Irei aqui focalizar a atenção para os detalhes a justificarem essa crucialidade do tema. Não há a pretensão em esgotá-lo, mas tão somente de reunir quesitos para tentar: 1) demonstrar a compatibilidade entre a polarização da luz com as teorias corpusculares; e 2) reunir argumentos a facilitarem a tarefa de emitir um juízo crítico a respeito da lógica de Dirac, assunto esse a ser abordado no último capítulo desta série.
VII.2 - A Polarização Absoluta
São muitas as evidências a nos convencerem de que a luz emitida por um único átomo, e num impulso único, esteja totalmente plano-polarizada, seja utilizando-se argumentos em acordo com a versão corpuscular newtoniana —interpretados da maneira exposta na figura 6 do capítulo I— seja utilizando-se argumentos em acordo versão de onda eletromagnética clássica —como mostrado na figura 10 do capítulo III. Existem também evidências —relatadas a partir de Newton, no século XVII— a demonstrarem que raios de luz "normal", propagando-se numa direção x e emitidos por fontes que sabemos hoje estarem dotadas de milhões desses átomos, podem ser divididos em dois outros raios secundários e a denotarem entre si características geométrico-espaciais diversas (lados dos raios de luz, segundo Newton). Um desses raios, por exemplo, poderá estar dotado de características a privilegiarem a direção de um eixo y perpendicular à direção de propagação x; neste caso, o outro privilegiará, por razões semelhantes, a direção do terceiro eixo cartesiano z. O eixo y (ou o eixo z) poderá ser escolhido arbitrariamente pelo observador do fenômeno. Existem, em teoria, infinitas duplas destes raios secundários, tantas quantos forem as possíveis orientações do eixo y, mas apenas uma dessas duplas manifestar-se-á em cada contexto experimental.
As dúvidas que surgem são do seguinte tipo:
- Esses raios secundários seriam totalmente equivalentes à luz emitida por um único átomo?
- Todos os constituintes elementares desses raios secundários seriam idênticos entre si, a privilegiarem uma direção arbitrária (y ou z)?
- Que dizer das demais direções, diferentes de y ou z mas também perpendiculares àquela do eixo x?
Essas perguntas poderão soar como sem sentido para aqueles que aceitam, sem restrições, as idéias expressas na imensa maioria dos livros didáticos da atualidade, a assumirem em definitivo a luz como sendo a propagação de um fenômeno eletromagnético, ou seja, nem corpuscular, nem mecânico-ondulatório. Neste caso, e na hipótese de o leitor se situar em meio a essa cômoda posição, peço vênia para prosseguir, pois com relação à física moderna as coisas parecem ser ligeiramente diferentes. A física moderna, de alguma maneira e através dos fótons, tem tentado recuperar a idéia de uma luz corpuscular, ainda que persista um fator de incerteza a caracterizar estes fótons, por vezes como puntiformes e, por outras, a espalharem-se segundo uma "onda" de natureza probabilística.
Ora, se pretendermos aqui questionar a física moderna e/ou as teorias que deram origem à física moderna, essas questões são fundamentais e devem ser respondidas, sob pena de passarmos para a história da ciência como aqueles que permaneceram inertes frente a uma acomodativa dogmatização da física de seu tempo. Direi então que existe uma polarizaçao absoluta e elementar, a caracterizar uma direção espacial, e uma polarização medial a privilegiar, sob um ponto de vista estritamente estatístico, uma região central, dentre um leque de possibilidades. Essa idéia, produto de uma convicção racional que venho defendendo desde 1983 [1], será apresentada no item a seguir.
VII.3 - A Polarização Medial
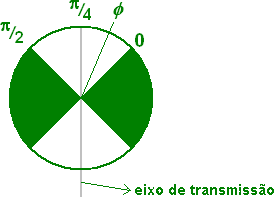
Determinados cristais apresentam um fenômeno chamado dicroísmo ou absorção seletiva da luz incidente. Característicamente absorvem, em condições ideais, praticamente 50% da intensidade da luz "normal" incidente numa direção perpendicular à de seu eixo de transmissão (qualquer eixo perpendicular ao eixo óptico do cristal). A luz propagada comporta-se de maneira a privilegiar uma certa direção perpendicular à direção de propagação.
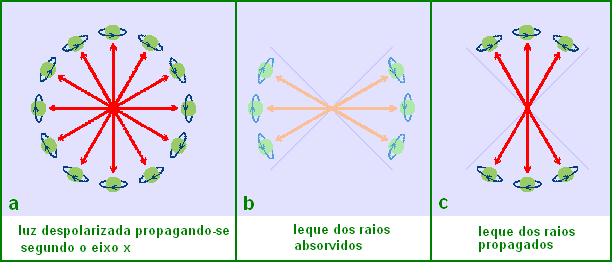
A figura 26 a representa um raio de luz "normal", ou despolarizada, desenhada da maneira convencionada no item III.4 do capítulo III (vide também a advertência feita ao final do item). Antes mesmo de ocorrer a absorção e a refração poderíamos pensar em representar aqueles corpúsculos (ou "ondas") que virão a ser absorvidos, como mostrado na figura 26 b, e aqueles que virão a se propagar pelo meio, como se vê na figura 26 c.
Figura 26: A luz corpuscular despolarizada (a), atravessando o plano da tela, e seus prováveis leques (b e c) a se comportarem diferentemente ao passarem por um cristal polarizador com eixo de transmissão situado na vertical.Vamos fixar a atenção no leque dos raios propagados (figura 26 c). Como irá se apresentar este leque após a refração ter se efetivado? Será que o leque se fechará totalmente, a ponto de podermos confundir este raio secundário como sendo totalmente equivalente à luz que seria emitida por um único átomo? (vide dúvida 1 apresentada acima). Se isto acontecer, poderemos sossegadamente afirmar que o cristal promoveu uma polarização absoluta ou total do raio transmitido. Do contrário poderemos, quando muito, afirmar que o raio está realmente polarizado segundo uma direção paralela ao eixo de transmissão, mas que esta polarização, pensada em termos elementares, tem um significado meramente estatístico. Ao que tudo indica, os corpúsculos (ou as "ondas") estão orientados, em média, segundo o eixo de transmissão do cristal (vertical no caso), mas na realidade a polarização absoluta, de fato, nunca acontece. Isso não é apenas uma convicção racional, mas uma afirmação a apoiar-se na experimentação, como será mostrado no próximo item.
VII.4 - Análise da Luz Polarizada
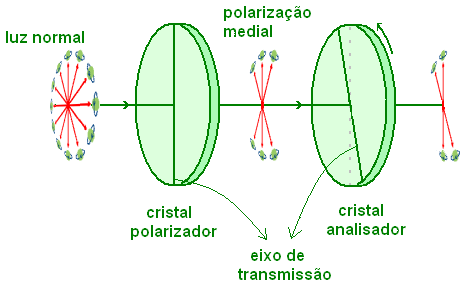
A análise da luz polarizada por um cristal dicróico pode ser efetuada da maneira representada na figura 27. Dois cristais dicróicos são dispostos de maneira a que seus eixos de transmissão sejam perpendiculares à luz incidente. O primeiro cristal, ou polarizador, permanece fixo durante a análise e o segundo cristal (analisador) gira em torno de um eixo a coincidir com a direção do raio de luz incidente. Compara-se a intensidade da luz que emerge do primeiro cristal (polarizador) com a intensidade da luz que emerge do segundo cristal (analisador), para cada ângulo entre os eixos de transmissão dos cristais, de zero a noventa graus.
Figura 27: Equipamento destinado à análise da luz polarizada. O primeiro cristal polariza a luz "normal" em uma determinada direção fixa (neste caso na direção vertical). O segundo cristal gira em torno da direção de propagação da luz. Compara-se a intensidade da luz que emerge do primeiro cristal (polarizador) com aquela que emerge do segundo cristal (analisador), para ângulos diversos entre os eixos de transmissão dos dois cristais.A figura 27 mostra que metade da luz que incide sobre o cristal analisador é absorvida e a outra metade é refratada. Isto é o que se observa experimentalmente, ou melhor, é o que se extrapola para uma idealidade teórica a partir de uma realidade experimental.
À medida em que o ângulo entre os eixos de transmissão dos dois cristais varia de 0º a 90º, a transmissão da luz no segundo cristal varia de 100% (condição ideal) do valor incidente a 0%, passando por todos os valores intermediários. Ora, se a luz estivesse realmente polarizada de maneira absoluta, não deveriam existir valores intermediários: ou ela seria 100% transmitida, ou então seria 0% transmitida. Experimentalmente está mais do que comprovado que esses raios de luz, a que chamamos polarizados, estão polarizados tão somente num sentido estatístico (ou médio, ou medial) a diferir enormemente da luz emitida pelo impulso único de "um" átomo. Em outras palavras, os fótons de uma luz com polarização medial não são idênticos entre si, havendo uma infinidade de fótons diferentes, assim como existem infinitos ângulos possíveis entre 0º e 90º ou assim como existem infinitos valores percentuais entre 0% e 100%. Estamos pois frente a uma outra condição em que o que se mede é um dado populacional e não um dado individual, devendo-se pois interpretá-lo sob o crivo do teorema da indeterminação, um teorema tão óbvio quanto desconhecido [2].
VII.5 - O efeito Malus (1809)
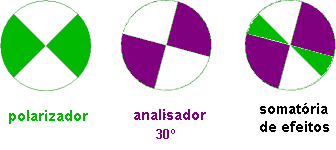
Se refinarmos um pouco a análise da luz polarizada, proposta no item anterior, inevitavelmente chegaremos na Lei de Malus. A análise exposta no item anterior justifica-se qualitativamente, mas existem condições outras a modificarem um raio de luz, quando este atravessa um cristal polarizador. Por exemplo, a intensidade da luz que emerge do segundo polarizador não é exatamente aquela que seria esperada caso efetuássemos uma ingênua somatória dos efeitos sobre os leques aí apresentados. A figura 28 servirá para ilustrar essa idéia, a ser apresentada a seguir.
Figura 28: Explicação no texto.Na figura 28 temos, à esquerda, a representação do efeito de um cristal polarizador sobre um raio de luz normal. Os leques em branco correspondem à luz "normal" que atravessa o cristal (pensando-se da maneira convencionada no item III-4, a incluir a advertência final), e os leques esverdeados correspondem à luz absorvida. No centro da figura 28 temos um segundo cristal também polarizador, idêntico ao primeiro mas chamado analisador, com a finalidade de se realçar a função desempenhada no equipamento experimental. Esse segundo cristal está com o eixo de transmissão girado em 30º, em relação ao eixo correspondente do primeiro cristal. Os leques em branco correspondem à luz "normal" que atravessaria esse cristal chamado analisador, e os leques em roxo correspondem à luz "normal" que seria absorvida por esse cristal. Somando-se os efeitos, como mostrado à direita da figura, os leques em branco resultantes terão um ângulo de 60º. Poderíamos então pensar que a luz transmitida pelos dois cristais deveria ter uma intensidade igual a 66% da luz que emergiu pelo cristal chamado polarizador, pois 60º representa 66% de 90º. Isso não acontece na prática, tendo sido demonstrado por Malus, em 1809, que para o caso específico (ângulo de 30º entre os eixos de transmissão) a transmissão da luz pelos dois cristais é igual a 75% da luz que emergiu do primeiro cristal. Podemos então concluir que a luz que emerge do primeiro cristal sofre alguma outra transformação ao passar pelo mesmo, além daquela relacionada à absorção de uma de suas metades, e a essa transformação deveria dar-se o nome de efeito Malus. Qual seria a causa desse efeito Malus?
VII.6 - A explicação corpuscular do efeito Malus
Vamos pensar na "luz monocromática normal" como aquela dotada de um número muito grande de corpúsculos e com uma distribuição ao acaso de suas propriedades. Estamos aqui admitindo a existência desses corpúsculos e tais que possam ser representados individualmente da maneira mostrada na figura 4 do capítulo I. Seja então um hipotético raio dessa "luz monocromática normal" a atravessar uma área unitária de uma superfície (por exemplo, o plano da tela) durante um intervalo de tempo também unitário.
Vamos agora fixar uma direção de referência (por exemplo, uma linha horizontal da tela) e nos questionar sobre: Quantos corpúsculos, dentre aqueles que atravessam essa unidade de área na unidade de tempo, têm seus eixos de giro orientados segundo um ângulo θ em relação à direção escolhida? A figura 13 do capítulo III, ou a correspondente figura 26a deste capítulo, poderão ajudá-lo a entender o que está por trás desse questionamento. Está surgindo aqui a idéia de uma densidade linear de números de corpúsculos, conforme a orientação espacial de seus giros segundo os raios de uma circunferência, digamos, de raio unitário. Ou melhor, estou propondo a idéia da existência de uma propriedade matemática, a ser incorporada ao estudo da distribuição dos corpúsculos nos raios de luz, a ser chamada densidade angular e definida através de uma relação entre números de corpúsculos e intervalos angulares, ou seja, algo do tipo:
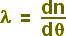
- (1)
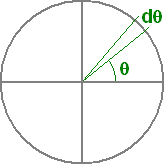
sendo dn o número de corpúsculos com eixo de giro situados radialmente entre os ângulos θ e θ + dθ, representados na figura 29.
Figura 29: Citada em correspondência com argumentos do texto.Conclui-se, por argumentos relacionados à isotropia, que a densidade angular l da "luz normal" deve ser a mesma em todas as direções, podendo-se facilmente calcular seu valor como sendo igual a N/2p, ou seja:
-
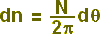
- (2)
N representa o número total de corpúsculos que atravessam a área unitária no intervalo de tempo unitário, algo intimamente relacionado com a intensidade da "luz monocromática normal".
Sob essas condições, e como veremos a seguir, demonstra-se que a lei de Malus pode ser expressa, em função dessa densidade angular l, da seguinte maneira:
-
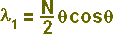
- (3)
ou seja, após passar pelo cristal polarizador (e daí o índice 1 de l), a "luz normal" sofre modificações estruturais tais que a distribuição dos corpúsculos, segundo o gráfico de densidade angular, não é mais uniforme e de valor igual a N/2p em todas as direções propagadas, mas sim variável como mostra a expressão (3) para um l1 pontual e a corresponder ao ângulo θ.
Estou assumindo que cada corpúsculo estaria como que sendo submetido a um torque capaz de reduzir a obliquidade entre o seu eixo de giro e o eixo de transmissão do cristal, e tanto mais quanto mais o ângulo entre esses dois eixos estiver próximo de p/2. Na representação gráfica proposta, isso promove um aumento da densidade angular dos corpúsculos no centro dos leques brancos e uma consequente redução nas bordas.
A expressão (3) pode também ser escrita em termos de dn e dθ:
-
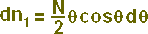
- (4)
Podemos efetuar a integração [3] da expressão (4) segundo os leques brancos (luz transmitida) apresentados para o cristal polarizador, conforme a figura 28 e com os ângulos definidos conforme a figura 30.
Figura 30: Explicação no textoFixando-se o ponto inicial da integração (ângulo = 0 rad) como mostrado na figura 30, e integrando a expressão (4) para todo um leque, do ângulo 0 a um ângulo arbitrário f, chegamos na expressão geral
-
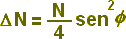
- (5)
válida para f variando de 0 a p/2 (figura 30), e com ΔN representando o número de corpúsculos que emergiram do polarizador e a serem representados graficamente entre os ângulos considerados (0 e f). Pensemos agora no ângulo f como sendo aquele ângulo entre os eixos de transmissão dos dois cristais, polarizador e analisador, mostrado na figura 28. Neste caso, o efeito do cristal analisador é exatamente o de extrair (ou absorver) o dobro desta fração de corpúsculos emergentes do cristal polarizador contida entre os ângulos 0 e f. É o dobro pois deve ser considerado também o leque inferior mostrado na figura 30, e a contribuir com uma fração idêntica.
Assim como chamamos de N o número de corpúsculos contidos na "luz monocromática normal" que atravessa a unidade de área na unidade de tempo, podemos assumir que este N irá gerar um N1 (correspondendo aos corpúsculos que atravessam o cristal polarizador) e um N2 (idem, que atravessam tanto o cristal polarizador quanto o analisador). Já afirmamos que em condições ideais o polarizador sozinho absorve 50% da "luz normal", e isso está em acordo com o resultado que seria obtido ao integrarmos a expressão (4) para os dois leques em branco da figura 30. É fácil perceber, da expressão geral (5), que para f = p/2, o ΔN será igual a N/4 e, nestas condições, 2ΔN será igual a N/2, o que corresponde a 50% de N.
N é uma entidade hipotética e compatível com a idéia de luz corpuscular. Na prática o que se mede é a intensidade da luz. E esta, pela hipótese assumida na definição de N, e considerando-se que estamos trabalhando com luz monocromática, deve ser diretamente proporcional a N. Consequentemente, podemos escrever
-
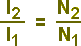
- (6)
Como vimos, N1 é igual a N/2 e N2 é igual a N1 menos uma fração absorvida que se iguala ao dobro do valor obtido pela equação 5. Portanto
-

- (7)
o que é o mesmo que escrever
-

- (8)
Esta nada mais é senão a equação a expressar a Lei de Malus no contexto tradicional, o que justifica a suposição feita acima a anteceder a apresentação da equação (3).
VIII.1 - Fótons e corpúsculos de luz
Antes de prosseguir, seria a hora de deixar claro o porquê, durante o transcorrer de quase todo o artigo, e sempre que possível, evitei a utilização da expressão fóton. Ora, o fóton não foi criado no seio de uma teoria corpuscular da luz. Em suas origens o fóton destinou-se a representar uma quantidade de energia transportada pelo que se convencionou chamar pacotes elementares de luz. A existência desses pacotes caracteriza a natureza corpuscular da luz, mas não implica necessariamente na aceitação desses pacotes como sendo a unidade corpuscular elementar da luz. Trata-se de uma entidade quântica, é verdade, mas nada que não possa ser explicado por uma quantização clássica, explicação essa que exaustivamente, e sem sucesso, foi procurada por Planck, tão logo se deu conta da maneira como seu trabalho original estava sendo interpretado (vide, por exemplo, a citação exposta no cabeçalho do capítulo IV).
O elétron, por exemplo, ao saltar de uma órbita para outra, envia para o espaço uma quantidade imensa de corpúsculos de luz, de maneira quase instantânea, porém num intervalo de tempo não exatamente nulo. O conjunto de todos esses corpúsculos, lançados durante um único impulso, nada mais é do que o que se convencionou chamar por fóton. Esse conjunto tem uma energia bem determinada hn. Bem determinada não por uma exigência relacionada à natureza corpuscular da luz, mas sim por restrições naturalmente impostas à partícula emissora: o elétron, para se acomodar em sua nova órbita, não pode lançar nem mais, nem menos do que o correspondente a esta energia hn.
Em outras palavras: Os corpúsculos elementares de luz podem ser pensados como partículas únicas, esféricas ou não, e a girar em torno de seu eixo. Um grande número desses corpúsculos, caminhando um atrás do outro conforme a figura 6 —e conservando entre si uma distância a relacionar-se à chamada frequência n da luz— desde que emitidos por um único elétron num único impulso, poderá se adaptar ao que se convencionou chamar por fóton, nos livros de física moderna.
Nos itens abaixo irei me reportar aos fótons da teoria quântica e é importante ter em mente essa distinção, pois iremos comparar comportamentos quânticos desses fótons com possíveis comportamentos clássicos denotados pelo conjunto dos corpúsculos que constituem esses pacotes quânticos.
VIII.2 - Suposições diracianas
Paul Adrien Maurice Dirac, ao propor um roteiro para chegar no que chamou Princípio da Superposição de Estados, levou em consideração alguns casos particulares e, dentre esses, privilegiou, dada a sua extrema importância, inúmeros aspectos relativos ao estudo da polarização da luz. Em seu trabalho chega a assumir que as propriedades de polarização da luz estão intimamente associadas com suas propriedades corpusculares, podendo-se atribuír a polarização aos fótons [1]. Não obstante, em todo seu texto deixa claro que não faz distinção alguma de natureza qualitativa entre o que chama raio de luz plano-polarizada e os fótons que poderiam eventualmente estar polarizados segundo esse plano. Ou seja, tudo nos faz crer que Dirac responderia à questão 1, formulada no item VII-2 deste artigo, assumindo uma total equivalência entre a luz emitida por um único átomo e um raio de luz que emerge de um cristal polarizador.
Nota-se, no trabalho de Dirac, uma preocupação desmesurada [2] em justificar a necessidade de uma teoria quântica frente a uma física clássica a seu ver:
- Inadequada para a explicação da notável estabilidade dos átomos e moléculas.
- Incompatível com as leis da espectroscopia.
- Incapaz de explicar os valores encontrados experimentalmente para o calor específico [3].
- Incapaz de explicar a aparente dualidade da luz. — Segundo Dirac, a interferência e a difração exigiriam explicações clássicas ondulatórias, enquanto o efeito fotoelétrico e o espalhamento Compton exigiriam explicações clássicas corpusculares.
- Incapaz de explicar um anômalo comportamento ondulatório de partículas elementares como o elétron.
Essas idéias não são apenas de Dirac, mas sim compartilhadas pela grande maioria dos físicos de seu tempo; e ainda hoje são repetidas pela imensa maioria dos livros didáticos ou, até mesmo, são reproduzidas em artigos científicos publicados em revistas respeitáveis. Ou seja, são suposições que acabaram sendo consagradas como verdades incontestáveis e, como tais, são ensinadas nas melhores universidades da atualidade.
VIII.3 - Estados de Polarização
Ao aceitarmos a hipótese da equivalência quase total [4] entre a luz emitida por um único átomo —ou seja, um fóton— e um raio de luz originalmente "normal", mas que acabou de passar por um polarizador, ficamos num impasse:
- A hipótese incompatibiliza-se com a experimentação, como mostramos no capítulo anterior (experiência discutida no item VII.4);
- A hipótese obriga-nos a criação de outra hipótese e esta, sem dúvida alguma, seria uma hipótese ad hoc.
Pelo visto, Dirac sentiu-se nesse impasse e fez uma opção: optou pela aceitação de uma nova hipótese, o da existência dos "estados" de polarização dos fótons. Através desse artifício conseguiu ludibriar os resultados de uma experiência que apontavam para outra direção. Vamos então tentar entender o que sejam esses "estados" de polarização.
Suponhamos que um raio de luz "normal", após ter passado por um cristal polarizador, transformou-se num raio absolutamente plano-polarizado segundo uma direção z. O plano a ser considerado no exemplo a seguir será aquele perpendicular a tela, interceptando esta em uma de suas verticais a representar o eixo z. Por absolutamente polarizado estou assumindo a hipótese (conforme exposto no item VII.2) de que todos os seus fótons seriam idênticos com respeito ao fenômeno polarização (corresponde portanto à hipótese da equivalência citada acima, no início deste item). Se eles são idênticos, podem ser representados por um artifício único, por exemplo, uma flecha (figura 31a). A escolha da flecha será justificada nos parágrafos a seguir.
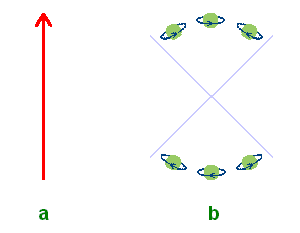
Figura 31: Representação dos fótons de um raio de luz plano-polarizada segundo:
a) a teoria quântica atual;
b) uma teoria corpuscular clássica.Embora os fótons tenham sido considerados por hipótese como iguais, a experiência mostra que eles comportam-se de maneira diferente ao atravessarem um segundo cristal polarizador. Se este segundo cristal tiver o seu eixo de transmissão formando um ângulo f com a direção z, uma fração percentual igual a sen2f do total desses fótons será absorvida pelo cristal, enquanto a fração restante, igual a cos2f, atravessará o cristal (Lembrar que sen2f + cos2f = 1 = 100%). Ora, como explicar essa diferença frente a uma identidade absoluta? Isso jamais seria compatível com qualquer raciocínio assumidamente clássico. Classicamente, e com base na experimentação, os fótons jamais poderiam ser supostos como idênticos. Mas a teoria quântica vai além dessa lógica clássica, e propõe a hipótese dos "estados" de polarização. O que seria isso, frente ao exemplo apresentado?
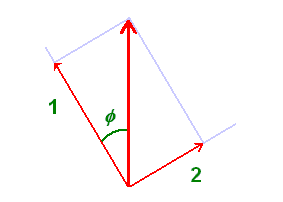
Ao escolhermos um ângulo f para posicionarmos o segundo cristal polarizador, estaríamos, de acordo com a teoria quântica, como que caracterizando a existência de dois "estados" possíveis para cada fóton do raio de luz a incidir neste polarizador. Os fótons continuam idênticos entre si, pois todos coexistem nesses mesmos dois estados fixados pelo observador ao escolher o ângulo f. Esses estados podem ser representados projetando-se a flecha da figura 31a em duas direções: uma correspondente ao eixo de transmissão do cristal e a outra numa direção perpendicular tanto ao eixo de transmissão quanto à direção de propagação da luz (figura 32).
Figura 32: Representação dos dois estados de polarização (1 e 2) de fótons pertencentes a raios de luz plano-polarizada na direção z e na iminência de penetrarem em um segundo polarizador com eixo de transmissão segundo um ângulo f em relação a z.Segundo Dirac, nós estaríamos submetendo o fóton a uma observação (passagem pelo segundo cristal polarizador). O efeito de fazer esta observação seria o de forçar o fóton a assumir um estado entre os dois possíveis. Ou o fóton assumiria inteiramente o estado 1, atravessando o cristal, ou assumiria inteiramente o estado 2, sendo absorvido pelo cristal. Este "salto quântico" de estados, entre um estado original para outro, dentre os dois possíveis estados quânticos, seria governado pelas leis das probabilidades, a se relacionarem ao quadrado do cosseno (estado 1) ou do seno (estado 2) do ângulo f.
É interessante observar que embora Dirac afirme inicialmente que a polarização da luz está intimamente associada a propriedades corpusculares, e durante toda a exposição da idéia apóie-se na noção de "pacotes" energéticos chamados fótons, chega a uma conclusão final que somente se justificaria classicamente se a luz fosse realmente uma "onda eletromagnética". Mas isso ele não poderia assumir de início, pois essa idéia de "onda eletromagnética" clássica não passaria pelo crivo da experimentação, logo toda a sua argumentação se esfacelaria. Tomando os devidos cuidados, Dirac instituiu uma nova hipótese ad hoc que, se por um lado negava a existência das ondas eletromagnéticas clássicas, por outro instaurava um novo período histórico para o eletromagnetismo, qual seja, a era da eletrodinâmica quântica. A aceitarmos essa hipótese, implicitamente estaremos aceitando a idéia de que na realidade os fótons não estão nem em um estado, nem no outro, mas ao prosseguir por seu caminho, submetem-se a uma lei que não difere muito daquela que controla o resultado do jogo de dados.
VIII.4 - Conclusão Final
Não é difícil comprovar a beleza do princípio da superposição de estados, nem tampouco generalizar sua aplicação para outros sistemas microscópicos [5], razão principal de ser da teoria quântica como interpretada na atualidade. Acredito mesmo que não seria difícil conseguir generalizá-lo para outros sistemas de todas as áreas do conhecimento. Mas a essência dessa natureza problemática da vitória da teoria ondulatória [6] não reside na veracidade do princípio, e sim na resposta que certamente um dia virá a ser dada para o seguinte questionamento: Existem de fato esses "estados" quânticos de Dirac? Até hoje ninguém respondeu a essa pergunta de maneira satisfatória pois, parafraseando Sokal, quanto mais estudamos a teoria quântica menos a entendemos [7]. A teoria quântica realmente consegue sobrepor entidades imaginárias a ponto de nos fornecer um modelo que funciona. Mas funciona sem que se saiba efetivamente como, quando, onde e nem porquê. E isso é muito mal, pois se por um lado ela nos satisfaz, ainda que em condições muito precárias, por outro tem prestado um enorme desserviço à comunidade científica, ao nos pretender convencer ser impossível decifrar a realidade íntima da matéria.
* * * * *
- MESQUITA F.°, A. (1987): Confesso que blefei — Física antiga × moderna (capítulo 25 — A polarização), Editora da USJT, São Paulo. O assunto chegou também a ser ligeiramente comentado na thread Teorias realistas atuais da Ciencialist, em abril-junho de 2000.
- MESQUITA F.°, A. (2000): Considerações Sobre a Incerteza, Espaço Científico Cultural.
- Lembrar que d(sen2θ) = 2θd(senθ) = 2θcosθdθ. Portanto, θcosθdθ = d(sen2θ)/2.
- DIRAC, P.A.M. (1967): The Principles of Quantum Mechanics, fourth edition (revised), Oxford Science Publications.
- Comento alguma coisa a esse respeito em O modelo mecânico newtoniano ou clássico.
- Comento alguma coisa a esse respeito em Calor específico e física clássica.
- Eu digo "quase" porque existe uma diferença aceita implicitamente: um raio de luz contém mais do que um fóton. O que a hipótese afirma é que todos os fótons de um raio de luz plano-polarizada seriam idênticos com respeito ao fenômeno polarização.
- FITZPATRICK, R. (1995): The fundamental principles of quantum mechanics. The principle of superposition of states: Any microscopic system (i.e. an atom, molecule, or particle) in a given state can be regarded as being partly in each of two or more other states. In other words, any state can be regarded as a superposition of two or more other states, in an infinite number of different ways.
- EINSTEIN e INFELD: vide item VI.1.
- Entrevista concedida por Alan SOKAL a Alessandro Grego e publicada em Homens de Ciência, Conrad Editora do Brasil Ltda, São Paulo, 2001.