O Modelo Mecânico Newtoniano ou Clássico
I — Introdução
A origem da mecânica clássica remonta a Galileu. Sua obra contém os principais alicerces sobre os quais se assentou a física newtoniana. As hipóteses fundamentais, a consubstanciarem o que chamamos modelo mecânico newtoniano ou clássico, são três e, da maneira como foram concebidas, logo adquiriram o status e/ou foram promovidas à categoria de leis ou de princípios.
Não tenho a pretensão de esmiuçar a evolução histórica da mecânica, mas, tão somente, resumir os avanços observados, sob uma ordenação lógica, de fácil compreensão e, acima de tudo, focalizar a atenção para possíveis recursos que, de alguma maneira, ficaram perdidos no tempo. Recursos esses, a meu ver, extremamente importantes e essenciais para quem quer que pretenda encarar seriamente a proposta de verificar se ainda há algo a ser desenvolvido em meio ao legado deixado pelos grandes físicos clássicos dos séculos XVII a XIX.
A proposta básica deste artigo será então a de tentar fornecer subsídios para que se possa responder ao seguinte questionamento: Existe algum sentido em procurarmos, hoje, por uma "moderna" física clássica? Acredito que a resposta será positiva e está à espera de ser encontrada em algum lugar do passado, ao vasculharmos o intervalo de tempo compreendido entre a apresentação do modelo mecânico newtoniano e o coroamento do modelo eletromagnético de Maxwell. Mesmo porque, as supostas fragilidades inerentes ao modelo mecânico clássico começaram a se evidenciar no final do século XIX, quando da tentativa de expandir o modelo eletromagnético para a interpretação dos fenômenos recém descobertos e relativos ao microcosmo, o mundo das partículas elementares.
Ao pensarmos em mecânica clássica e, em especial, na sua evolução de Newton a Maxwell, há que se distinguir pelo menos cinco características inter-relacionadas. São elas:
- O modelo mecânico propriamente dito.
- A matemática aplicável ao modelo mecânico.
- O modelo newtoniano no contexto da mecânica.
- A mecânica no contexto globalizante.
- O materialismo mecanicista.
Aspectos relevantes e associados a esses tópicos, em especial aos três primeiros, serão abordados neste artigo, a ser complementado por artigos outros a serem escritos oportunamente.
II — O modelo mecânico propriamente dito
O modelo mecânico newtoniano, enquanto modelo, é uma obra acabada e redutível a três leis de movimento. Estas, por sua vez, sintetizam conhecimentos passíveis de verificação através de experiências nas quais o fenômeno estudado é o movimento de objetos que, de alguma forma, sensibilizam nossos órgãos dos sentidos, diretamente ou através de equipamentos laboratoriais. As leis foram propostas, como hipóteses, sob um clima de realismo transcendental, ou seja, com a pretensão —daí a transcendência— de que se sujeitassem a uma universalidade espaço-temporal —e daí o realismo.
A mecânica genuinamente newtoniana, como veremos oportunamente, é bem mais abrangente, acomodando outras facetas e, até mesmo, pressupostos, a constituírem um verdadeiro pano de fundo a comportar o modelo. As leis, quando interpretadas fora desse contexto globalizante, via de regra denotam uma certa fragilidade. E isso ocorre com muita frequência, pois o sucesso do modelo, com suas leis, chega a obscurecer o cenário no qual o mesmo teria sido plantado. A não observância do cenário, por um lado, denuncia pseudo fragilidades e, por outro, dá origem a interpretações dúbias.
Se o modelo mecânico inicialmente proposto permaneceu inalterável, o cenário sobre o qual ele se apoiou foi sofrendo alterações gradativas e progressivas. Sob esse aspecto poderíamos falar numa evolução ou, como afirma Dirac [1], em um desenvolvimento contínuo da mecânica clássica. Desenvolvimento esse processado às custas de uma modificação do cenário, nem sempre acompanhada da preocupação, manifestada por Newton, em acumular créditos afim de evitar o surgimento das aparentes fragilidades.
Ao que tudo indica o modelo, desde seu início, foi proposto como algo provisório e destinado a sintetizar elementos importantes e essenciais do ponto de vista operacional. Como tal, comporta várias matemáticas e várias idealizações, prestando-se também a tolerar simplificações supostamente válidas em condições específicas. Representaria, para seu autor, não exatamente uma teoria acabada, mas um conjunto completo de hipóteses amplamente testadas —e daí serem chamadas de leis ou princípios,— inter-relacionadas, passíveis de uma utilização imediata e a concordarem com uma teoria bem mais geral a ser completada em um futuro longínquo. A teoria propriamente dita teria sido então apresentada, nos Principia, como uma obra inacabada e repleta de lacunas, tanto de natureza teórica quanto experimental, e propositalmente deixadas para que fossem gradativamente esclarecidas por seus seguidores. Isso está explícito em toda a obra de Newton, tanto nos Principia quanto em sua Óptica ou mesmo em cartas que escreveu a amigos. Digno de nota é o comentário seguinte, deixado em meio a uma infinidade de outras considerações relevantes, a fazer parte de um dos últimos parágrafos de sua magistral Óptica: "E, portanto, não tenho escrúpulos em propor os princípios de movimento acima mencionados, sendo eles de uma extensão muito geral, e deixar suas causas serem descobertas"[2]. Ou então, esta mini síntese autobiográfica, escrita nos últimos anos de sua vida e a retratar o quão ciente estava do caráter incompleto de sua obra: "Não sei de que modo o mundo me vê; mas a mim mesmo pareço ter sido apenas um menino brincando na praia, entretendo-me com encontrar de quando em quando um seixo mais liso ou uma concha mais bela do que o ordinário enquanto todo o vasto oceano da verdade jazia inexplorado diante de mim."
Curiosamente, nos dias atuais, quando se fala em física newtoniana, quase sempre pensa-se tão somente no modelo mecânico e que, sem dúvida alguma, é abrangente, completo e magnífico, mas, acima de tudo, proposto por Newton com a expectativa de que viesse um dia a ser substituído por algo melhor, a apoiar-se em conceitos rígidos e inerentes ao restante de sua física; e a acontecer tão logo as causas, a responderem por suas leis (ou princípios), fossem descobertas. Mas... O que seria esse "restante de sua física" —supostamente modificado para dar origem ao que chamamos hoje por física clássica— a caminhar lentamente para a obsolescência? E o que seria esse "algo melhor"? Será que Newton previu a evolução de sua física para algo semelhante à chamada física moderna do século XX?
III — A matemática aplicável ao modelo mecânico
A começar com Galileu, matemática e física sempre andaram de mãos dadas e, sob esse aspecto, o modelo mecânico sofreu adaptações profundas no decorrer do tempo. Não obstante, e a despeito da multiplicidade de formalismos que foram surgindo, o modelo conservou a sua essência.
A concomitância entre o alvorecer da mecânica clássica e a invenção do cálculo diferencial e infinitesimal não foi obra do acaso. O conceito intuitivo de limite, por exemplo, paira por toda a obra de Galileu; e tanto assim é que as leis, que surgiram em decorrência de seus ensinamentos, eram todas leis ideais, ou seja, válidas em condições limites. A perícia do experimentador consistia exatamente em aproximar a realidade da idealidade, através da redução dos fatores responsáveis pelos desvios observados entre a expectativa teórica e o que realmente se encontrava na prática. Exemplos: 1) lubrificando-se uma superfície horizontal, reduz-se o atrito entre a superfície e um objeto que por ela desliza e, nestas condições, percebe-se que velocidade do objeto tende a um valor limite constante, à medida em que o atrito tende a zero; 2) extraindo-se o ar de um recipiente nota-se que objetos de massas e formatos diferentes, caem obedecendo a mesma equação horária, ou seja, à medida em que a pressão do meio ambiente tende a zero, o movimento tende a um padrão limite bem definido e a ser expresso pela lei da queda livre. Essas idéias, ao lado de outras, acabaram sendo matematizadas por Leibniz e Newton, e o conceito de limite ganhou em objetividade, surgindo gradativamente as noções de infinitésimo, de integração e de diferenciais a consubstanciarem o que chamamos hoje por Cálculo Diferencial e Integral.
Os diversos formalismos foram sendo desenvolvidos pari passu com a concepção dos chamados construtos de alto nível, cujo exemplo típico é a energia. Graças a esses construtos, fica-se às vezes com a falsa impressão de que existem vários modelos diferentes e a serem aplicados em condições específicas. Nada mais falso pois os formalismos não são mutuamente exclusivos e, quando gerais, pode-se sempre partir de um e deduzir o outro ou vice-versa.
A evolução matemática também observou um desenvolvimento contínuo. E tanto isso é verdade que a pedagogia repete a história: o aluno secundarista aprende, via de regra, um formalismo matemático no estilo newtoniano, ainda que por demais elementar e a apoiar-se fundamentalmente no conceito de força. A partir de então chega aos princípios de conservação, deduzidos a partir das leis gerais enunciadas da maneira proposta por Newton e já assimiladas pelo aluno no seu primeiro contato com a matéria. Alguns anos após, já na universidade, é induzido a esmerar-se na aplicação do Cálculo, com o que espera-se que venha a entender o modelo em toda a sua extensão. Após essa iniciação, vai sendo apresentado gradativamente aos demais formalismos matemáticos, em especial o lagrangeano e o hamiltoniano. O primeiro tem se mostrado útil ao fornecer algoritmos extremamente elegantes e, acima de tudo, eficazes para o equacionamento e resolução de inúmeras situações à primeira vista bastante complicadas, enquanto que o formalismo hamiltoniano vai um pouco além e, conquanto tenha sido desenvolvido no século XIX, em pleno apogeu da mecânica clássica, costuma ser descrito como aquele que usa a mesma linguagem para descrever os sistemas dinâmicos, tanto na teoria quântica, quanto na teoria clássica (Dirac [3]). Com frequência enfatiza-se esta propriedade matemática afirmando-se que o formalismo hamiltoniano fornece a rota para a quantização [4].
Esta evolução da física clássica para a teoria quântica, que sob o ponto de vista da matemática parece-nos bastante natural, quando analisada sob o ponto de vista físico retrata o cisma que ocorreu na física, logo após um período de crise na física clássica. Assim é que Dirac [5] refere-se a um novo esquema a adequar-se a fenômenos na escala atômica. Por novo esquema, entenda-se um novo modelo não vinculado à essência do modelo mecânico newtoniano e, também, totalmente alheio ao que poderíamos chamar física newtoniana. Não existe mais o cenário clássico a comportar o modelo clássico. Em seu lugar surge um ambiente nebuloso, a comportar um conjunto de equações que dão certo, equações estas que, em condições especiais, reduzem-se às equações do modelo clássico. A nebulosidade transparece nas entrelinhas de outro pensamento de Dirac citado por Herrera[6] (1983): Parece que ao se trabalhar a partir do ponto de vista de obter beleza nas equações e tendo-se intuição, se está numa linha segura de progresso. A falta de clareza inerente ao modelo chega a ser compensada por um caráter subjetivo, qual seja, a beleza matemática aliada à funcionalidade e à esperança de uma compreensão futura, a configurarem um questionável progresso.
A satisfação aparente, manifestada por Dirac, não é compartilhada por todos os construtores da física quântica. Planck, por exemplo, jamais se conformou com o caráter fisicamente ininteligível das equações que, curiosamente, encerram uma constante universal a levar o seu nome. Caráter esse que chegou a ser muito bem descrito por um físico da atualidade, Alan Sokal, com as seguintes palavras: ...Já a teoria da física quântica é muito complicada, e nem os físicos têm certeza do que ela significa. E tenho de confessar que, quanto mais eu estudo teoria quântica, menos eu a entendo [7]. Schrödinger [8], por outro lado, acreditava em uma reviravolta a conduzir finalmente a algo melhor do que as confusas séries de fórmulas que cercam o nosso tema; e a principal destas fórmulas nada mais é senão a chamada equação de Schrödinger. Entre a satisfação manifestada por Dirac e a insatisfação denunciada por Planck e Schrödinger, realça a indiferença de Bohr, segundo o qual é possível prescindir de uma concepção completa e manifesta da realidade, limitando-se à formulação matemática de um fenômeno [9].
Sem dúvida, num aspecto todos são concordes: o modelo quântico funciona sem que se saiba onde, quando e nem porquê [10]; e quando de seu reducionismo, chega a dar origem às equações do modelo clássico, agora não mais suportadas pelos pressupostos newtonianos, mas soltas no espaço e sem cenário algum a justificá-las, o que teria sido expresso por Einstein e Infeld com as seguintes palavras: A mecânica clássica flutua no ar [11].
IV — O modelo newtoniano no contexto da mecânica
IV-1 O que é mecânica?
De maneira bastante resumida, podemos dizer que a mecânica clássica é o estudo do movimento da matéria tendo por base a experimentação; e a experimentação presta-se não apenas como fonte de informações confiáveis mas, também, como o terreno adequado onde se processam as corroborações ou os falseamentos das hipóteses ou das previsões logicamente concebidas. Via de regra começa-se o estudo da mecânica pela cinemática, mas esta nada mais é senão um capítulo introdutório e destinado a caracterizar o movimento ou a definir as suas propriedades básicas. Conhecidas estas propriedades, vêm-nos à mente questões fundamentais, como aquelas do tipo: Porque em determinadas condições a velocidade de um corpo mantém-se constante no decorrer do tempo enquanto que em outras sua velocidade é variável? Ou, então: Porque os corpos lançados no espaço adquirem, em determinadas condições, uma trajetória curva? Questões como essas são respondidas pela dinâmica e a dinâmica clássica começa pela caracterização do modelo mecânico newtoniano através de três leis do movimento.
A dinâmica, seja relacionada ao movimento —dinâmica propriamente dita,— seja focalizada a estudar outros fenômenos naturais, como é o caso da termodinâmica ou da eletrodinâmica etc, envolve o estudo de interações. Consequentemente, a dinâmica propriamente dita estuda as interações entre os objetos no sentido de explorar as causas ou as consequências das possíveis modificações do estado de movimento dos mesmos. Esse estado é avaliado por suas propriedades mecânicas, em geral aquelas estudadas em cinemática ou, então, associações entre as mesmas.
A simples observação dos objetos familiares sugere a existência de dois tipos importantes de interação mecânica: a interação por contato direto e a interação a distância. Ao frearmos um automóvel, por exemplo, iniciamos um processo de interações por contato e em série; por outro lado, ao soltarmos uma pedra no espaço, percebemos que ela cai sob o efeito de uma interação a distância (pedra-Terra). Puxar e empurrar são os vocábulos vulgares associados à interação por contato; atrair e repelir são os seus equivalentes, porém associados ao estudo das interações a distância. Empurrar, puxar, atrair e repelir são termos que associamos, intuitivamente, à noção de força. Com essa idéia intuitiva em mente, podemos falar em força de contato e em força de campo, a caracterizarem respectivamente a interação por contato direto e a interação a distância.
É importante entender que a idéia intuitiva de força, como algo a responder pela interação entre os objetos, precedeu à construção do modelo mecânico. Isso é importante porque a partir dessa idéia intuitiva somos levados a pensar no isolamento de um corpo como algo equivalente à condição em que o mesmo estaria livre da ação de forças. Foi a noção de isolamento, e não a ausência de forças em si, o pré-requisito básico utilizado na dedução da hipótese que levou Newton, após Galileu, a caminhar em direção a sua primeira lei, a lei da inércia. Ou seja, a primeira lei é a porta de entrada para a dinâmica e, como tal, retrata o comportamento a ser observado por um corpo que não esteja em interação com nenhum outro, ou seja, um corpo isolado ou, ainda, um corpo que possamos imaginar como não dotado daquela característica relacionada à interação com outros corpos e que nos leva a intuir o que seja força, mesmo antes de defini-la.
Pode-se também pensar na primeira lei como sendo um caso particular da segunda, ou seja, a primeira lei retrataria a segunda para o caso de força resultante nula. Isso, quando muito, pode ser encarado como uma verdade matemática, mas perde em conteúdo ao verificarmos que as leis de Newton são, na realidade, hipóteses a consubstanciarem um modelo teórico. Ora, hipóteses são deduzidas logicamente e não matematicamente. Como a dedução da segunda lei implicou na interpretação de observações relativas ao comportamento dos corpos, assumindo-se, dentre outros fatores, a veracidade da lei da inércia, percebe-se aqui o caráter essencial desta última e, como tal, necessário ao modelo mecânico da maneira como foi proposto. Digno de nota é o fato de a lei da inércia não se referir a corpos sujeitos a uma força resultante nula, mas a corpos totalmente livres da ação de agentes interativos e, consequentemente, de forças. Trata-se, portanto, de uma lei limite. Será tanto mais comprovada experimentalmente, quanto mais nos aproximarmos desse limite, qual seja, do isolamento perfeito.
IV-2 Da intuição ao modelo clássico
Porque a Lua não cai? Essa pergunta deve ter ocorrido a Newton quando, de seu pomar, avistou a Lua por detrás de uma macieira. A ser verdadeira essa suposição, teria visualizado maçãs e Lua lado a lado e, aparentemente, em repouso no espaço. Muito provavelmente deve ter se questionado:
— A maçã não cai graças ao pedúnculo. Mas... e a Lua? Porque não cai?
De acordo com a inércia de Galileu, acreditava-se, na época, que um corpo livre da ação de forças estaria ou em repouso, ou em movimento de translação circular. Nessas condições, e até prova em contrário, seria de se esperar uma órbita circular para a Lua, ao redor da Terra. Poder-se-ia então pensar que a Lua não cai por estar em movimento inercial e, portanto, livre da ação de forças.
— Mas... estaria a Lua livre da ação de forças? E a atração gravitacional? Não seria extensiva à Lua? E, neste caso, não seria de se esperar que ela caísse, a exemplo da maçã quando se corta o pedúnculo? Ou, melhor, como um objeto lançado no espaço que nos rodeia? Mas... e se pensarmos num movimento inercial não circular, mas... retilíneo?!!!
O insight newtoniano muito provavelmente foi algo desse tipo e, nestas condições, é bem possível que a lei da inércia, como a conhecemos hoje, tenha sido enunciada quase que intuitivamente. As outras duas leis, por sua vez, estavam como que "pedindo" para serem deduzidas, dedução esta a guardar íntima relação com uma outra lei, fora do escopo da mecânica, mas que também estava se mostrando intuitivamente, ainda que em forma latente, qual seja, a lei da atração gravitacional, intimamente relacionada à lei da queda livre de Galileu. Visto sob esse aspecto, percebe-se que o modelo mecânico surgiu da observação daquilo que hoje é considerado uma de suas aplicações: o estudo da interação à distância entre objetos, ou seja, uma interação mediada pela ação de "alguma coisa" relacionada ao que chamamos hoje campo de forças. A esse respeito, lê-se o seguinte, em uma das cartas de Newton: "É inconcebível que a matéria bruta inanimada possa, sem a mediação de alguma coisa, que não é material, atuar sobre, e afetar outra matéria sem contato mútuo, como deve ser, se a gravitação no sentido de Epicuro for essencial e inerente a ela. [12]"
IV-3 Colisões
A elegância e a simplicidade do modelo clássico é também observada no estudo das colisões entre objetos. Em linhas gerais, o processo pode ser subdividido em três etapas:
- aproximação;
- colisão ou choque propriamente dito; e
- afastamento.
A aproximação pode ocorrer com ou sem uma ação a distância apreciável e/ou mensurável. Num choque entre bolas de bilhar, por exemplo, podemos perfeitamente desprezar a atração gravitacional entre as duas bolas. Estudos mais sofisticados utilizam-se de pucks— objetos achatados e discóides— que colidem em cima de uma mesa horizontal dotada de um colchão de ar a evitar o contato —e daí o atrito— da mesa com o puck. Alguns desses pucks são magnetizados, podendo haver uma colisão entre dois deles num processo tal que a ação a distância chega a ser considerável.A fase de colisão, ou de choque propriamente dito, seria aquela em que os corpos chegam a se tocar no sentido macroscópico que se dá ao termo e isto, como veremos logo mais, deve ser interpretado com muito cuidado.
Quando o campo não é desprezível o resultado pode ser diverso conforme a força de interação a distância seja de atração, como por exemplo, a gravitacional, ou de repulsão, como por exemplo, a força magnética entre pólos semelhantes de imãs.
No caso da atração, se os corpos estiverem em rota de colisão haverá o choque propriamente dito; do contrário, se as trajetórias forem tais a ponto de os corpos se aproximarem sem que se preveja uma colisão propriamente dita, uma dentre duas coisas poderá acontecer: ou os corpos se afastam graças à inércia, tão logo tenham atingido o ponto de máxima aproximação, obviamente com suas trajetórias modificadas pela ação dos campos atrativos; ou eles entram em órbita, um ao redor do outro, constituindo então um conjunto binário. A utilização do modelo mecânico, com suas leis, permite a determinação do que irá acontecer, desde que se conheça as propriedades mecânicas iniciais dos dois corpos.
No caso da repulsão, como aquela observada com pucks magnetizados, se o campo magnético repulsivo for intenso, ou se a velocidade relativa for pequena, percebe-se que este contato íntimo deixa de existir, pois os pucks, após uma aproximação máxima, começam a se afastar sem se tocarem.
Quando o campo é desprezível e os corpos estão em rota de colisão, observa-se o choque propriamente dito ou o contato íntimo da matéria que os constitui. Havendo um contato íntimo, qualquer que seja o caso (com ou sem interação à distância) pode-se observar tanto o afastamento após a colisão, quanto o agrupamento ou a aglutinação dos corpos que se chocam, passando a constituírem um corpo único.
Rigorosamente falando, mesmo esta colisão em que os corpos se tocam no sentido macroscópico do termo, na realidade o que temos é um caso particular de interação à distância, ainda que esta fase, que estamos chamando por fase de contato íntimo, se dê a uma distância bastante pequena. As partículas elementares, que entram na constituição dos objetos macroscópicos, muito provavelmente não se tocam, na verdadeira acepção da palavra. Não obstante, tudo se passa como se houvesse esse contato direto durante um breve intervalo de tempo; intervalo esse tão pequeno a ponto de poder ser considerado nulo (interação instantânea).
Assumindo-se esta simplificação, não há também porque se falar em campo, podendo-se pensar na interação como tendo uma duração instantânea e também na força como sendo devida a uma propriedade pontual e bem localizável no espaço. Esta maneira de interpretar o problema, se bem que retrate uma idealidade, é respaldada pela experimentação.
Aceitando-se ou não esta simplificação, a verdade é que fica muito difícil, se bem que não impossível, raciocinar em termos de força com duração de ação tão pequena. Casos como este justificam a adoção do modelo mecânico em um formalismo a apoiar-se não nas leis de força mas em suas equivalentes leis de conservação, lembrando-se que é sempre possível partir de um dos conjuntos de leis e chegar matematicamente ao outro. Voltaremos a esse assunto ao comentarmos as leis de conservação, em artigos futuros —e ainda não escritos,— desta série.
Do ponto de vista teórico, além das simplificações assinaladas, de natureza espacial e temporal, costuma-se assumir, nos casos em que se dá o afastamento após a colisão, que o caráter puntiforme e instantâneo da ação acompanhe-se de outra idealização, agora de natureza estrutural, qual seja, uma hipotética e rígida impenetrabilidade da matéria. Deixa-se de se considerar a causa desta suposta impenetrabilidade ou a ocorrência de eventuais deformações —sejam estas momentâneas e reversíveis ou, então, permanentes— das superfícies dos objetos que se tocam.
Na grande maioria dos casos estudados, qualquer outra força é considerada desprezível. Costuma-se então afirmar que as únicas forças de interação são as forças de contato. As forças de contato, estudadas nas colisões de objetos macroscópicos, seriam aquelas a responderem pela transferência praticamente instantânea de momento (ou movimento, ou ainda, quantidade de movimento), transmissão esta assumida como efetuada de maneira brusca e não contínua.
É importante que se enfatize essas idealizações para que se perceba que não é apenas o modelo mecânico, com suas três leis, que está entrando em jogo. Em outras palavras: O que se observa, no nível macroscópico, nem sempre condiz com o que efetivamente está ocorrendo no microcosmo. Por outro lado, a interpretação de experiências relativas a fenômenos que ocorrem no microcosmo não pode, em hipótese alguma, adotar gratuitamente, ou seja, "a priori", a generalização das idealizações aqui apresentadas, sob o pretexto de que tais idealizações passaram pelo crivo da experimentação. A validade do argumento restringe-se tão somente ao estudo de objetos que nos são familiares pois, via de regra, é aí que temos a garantia da comprovação experimental. Observações de natureza indireta, ainda que bem documentadas, nem sempre nos autorizam a que extrapolemos estas idealizações —supostamente válidas— de um cenário bem conhecido para outro que pretendemos conhecer. Do contrário poderíamos concluir precipitadamente que o modelo mecânico —aqui simplificado por razões de natureza prática— nem sempre funciona bem no mundo das partículas elementares, e este é um tema que deve ser abordado com extrema cautela.
IV-4 Forças de contato
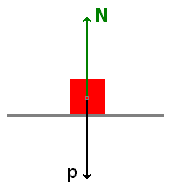
As forças de contato são extremamente úteis para que o iniciante entenda operacionalmente, e pela primeira vez, a lei da ação e reação, ao lado das outras duas leis. Sabemos, por exemplo, que um objeto em repouso sobre uma plataforma horizontal e situada no campo gravitacional terrestre, está sujeito à força peso, dirigida na vertical e para baixo. Não obstante está em repouso. Ora, se ele está em repouso, mas sujeito a ação de forças, é de se esperar, pela segunda lei, que a resultante das forças que agem sobre o corpo seja nula. Isto acontecerá se a plataforma aplicar ao corpo uma força normal (ou vertical), para cima e de mesma intensidade que a força peso (figura 1).
Figura 1: Corpo em repouso sobre uma
plataforma horizontal.Esta força normal deve surgir como reação à tentativa do corpo em entrar em movimento acelerado em obediência à atração gravitacional (ação primeira). A tentativa é frustrada graças à impenetrabilidade manifestada pela plataforma e esta impenetrabilidade traduz-se macroscopicamente por uma deformação da superfície, o que pode ser constatado através de um "ampliador óptico de deformações" [13]. Podemos então assumir a existência de uma força de reação N normal à superfície. É importante enfatizar que a ação referida na terceira lei não é o peso p em si, mas a força - N que o objeto exerce sobre a plataforma ao tentar atravessá-la e que, neste caso, é de mesma intensidade que o peso. Em outras palavras, as forças apresentadas na figura 1 não são ação e reação por duas razões: uma é que a reação N que plataforma exerce sobre o objeto relaciona-se, pela terceira lei, à ação - N que o objeto exerce sobre a plataforma, enquanto que o peso p é a ação que a Terra exerce sobre o objeto e, neste caso, a sua reação - p é a força, também de natureza gravitacional, que o objeto exerce sobre a Terra; e outra é que forças de ação e reação não podem estar aplicadas a um mesmo corpo. [14]
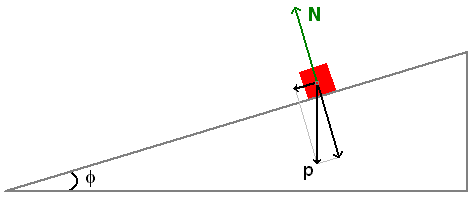
Podemos expandir a idéia para um objeto em movimento, devido ao peso, numa plataforma disposta de maneira a determinar um ângulo f com a horizontal, o chamado plano inclinado (figura 2), primeiramente utilizado por Galileu. Supondo o deslizamento sem atrito e, portanto, também sem rolamento, nota-se que o objeto, inicialmente em repouso, desloca-se para os pontos mais baixos da plataforma num movimento acelerado, porém com aceleração inferior à gravitacional. Se f for igual a zero, teremos o caso discutido acima (plataforma horizontal), com aceleração igual a zero e, portanto, o objeto, inicialmente em repouso, permanecerá em repouso; se f for igual a 90° teremos a queda livre, caso em que a aceleração iguala-se à gravitacional. Para valores intermediários de f, entre zero e 90° , teremos uma aceleração constante cujo valor dependerá da inclinação da plataforma segundo uma função senoidal em f.
Figura 2: Corpo em movimento sobre um plano inclinadoA força responsável por essa aceleração é o componente da força peso na direção do movimento. Como o objeto está sujeito também ao outro componente do peso, perpendicular ao movimento, e este —para um observador em repouso em relação ao plano inclinado—, não imprime aceleração alguma, a conclusão (segunda lei) é que o objeto deve estar sob o efeito de outra força de mesma intensidade e sentido contrário a esse componente da força peso. Esse nada mais é senão a reação N da plataforma à ação que o objeto exerce sobre a mesma e que, para f entre 0 e 90° , é inferior ao peso, segundo também uma função senoidal a depender da orientação da plataforma (neste caso, o argumento do seno é o complemento de f, percebendo-se facilmente que a função pode ser expressa em termos do co-seno de f).
Há de se notar que em grande número de casos, tanto nas colisões quanto no movimento de objetos localizados em cima de plataformas, o local de transmissão das forças de contato pode ser considerado como um ponto da superfície do objeto que está alinhado, na direção da força, com o centro de massa do objeto. Esta é uma outra simplificação, também devida a Galileu, válida naqueles casos em que, para o fenômeno estudado, podemos assumir o objeto de estudo como tendo toda a sua massa localizada no centro de massa. Ou seja, estamos assumindo uma característica puntiforme para o objeto, o que deve ser sempre efetuado com muito cuidado. Em particular, e para o caso da figura 2 acima, supondo-se a altura do objeto bem maior do que a largura, não é difícil concluir que neste caso ele poderia tombar sobre o plano inclinado.
Raciocinando-se classicamente, a realidade pode ser outra. Para cada força suposta agir sobre o centro de massa do corpo rígido, devem existir tantas forças microscópicas quantas forem as hipotéticas partículas classicamente elementares a comporem o corpo; e as interações são transmitidas entre partículas vizinhas, e assim sucessivamente, por toda a extensão do corpo rígido, de maneira a permitir que o efeito de superfície possa ser assumido como se aplicado diretamente sobre o centro de massa do corpo. A não definição do que sejam partículas classicamente elementares não invalida o argumento que poderia ser utilizado até mesmo supondo-se uma natureza contínua para a matéria, o que hoje sabemos não ocorrer.
Quando o objeto está situado num campo de forças, uma transmissão em cadeia deve também ocorrer e o efeito resultante, sob certos aspectos, pode ser considerado como agindo em seu centro de massa. Nestes casos, mesmo para corpos rígidos e extensos situados em campos não uniformes, podemos assumir a força como única, como determinável,
e a agir sobre um hipotético centro de massas.
Esta simplificação, de natureza geométrica, nem sempre é tão elementar quanto aqui descrita. Existem casos de interações por contato em que a resultante não passa pelo centro de massa. Nestas condições o objeto ficará sujeito a um torque a propiciar modificações de seu movimento de rotação. Por outro lado, o modelo clássico não assume, em suas hipóteses, a instantaneidade do que chamamos acima por transmissão em cadeia. Este é um assunto que não pode ser deixado de lado quando da tentativa de compatibilização entre o modelo mecânico clássico e efeitos observados experimentalmente e relacionados à relatividade clássica.
IV-5 Força de atrito
Se a plataforma assumida no exemplo da figura 2 não for suficientemente lisa, o corpo, para manter-se em movimento, deverá vencer as rugosidades e aderências que encontra pela frente. Neste caso, a força resultante que o corpo exerce sobre a plataforma, assim como a reação a esta força, não é mais perpendicular a superfície macroscópica, mas tem uma componente na direção do movimento. É sempre possível pensar-se nesta reação como composta por duas forças distintas: a normal à superfície, perpendicular ao movimento, e a chamada força de atrito, na direção do movimento e em sentido oposto ao mesmo. Essa última tem interesse no sentido em que retarda o movimento do corpo de prova. Se, por um lado, o componente da força peso, na direção do movimento (vide figura 2, acima), age no sentido de aumentar a velocidade do corpo, a força de atrito age no sentido oposto. A primeira, agrega energia cinética ou de movimento ao corpo, e daí dizermos que realiza um trabalho positivo. A segunda, contrapõe-se a essa agregação de energia cinética, realizando um trabalho negativo. A energia mecânica é perdida neste processo e transformada em calor e as forças que agem dessa maneira são chamadas dissipativas.
IV-6 Deformações ou movimento da plataforma
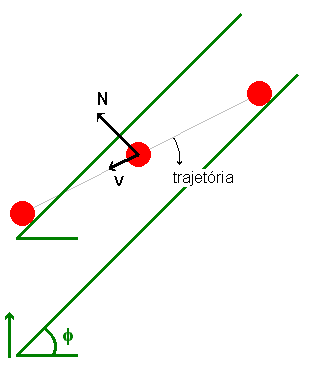
Se a plataforma estiver em movimento, digamos, elevando-se no campo gravitacional terrestre, a trajetória descrita pelo corpo em movimento não é mais paralela a sua superfície. Dependendo do tipo de movimento da plataforma, a trajetória pode assumir formatos os mais bizarros, mas a figura 3 representa a situação mais simples, em que a trajetória continua sendo retilínea. Neste caso a reação normal N realiza trabalho, pois colabora para um ganho de energia potencial pelo corpo em deslizamento. Com efeito, se não houvesse a elevação da plataforma, percebe-se, pela figura 3, que o corpo ocuparia, a cada instante, uma posição mais baixa do que aquela que está lá representada.
Figura 3: Trajetória de um objeto deslizando sobre um
plano inclinado em movimento.Plataformas deformáveis no decorrer do tempo, por motivos idênticos, também reagem ao contato de objetos extensos através de forças normais também em condições de realizar trabalho. Problemas desse tipo nem sempre são facilmente resolvidos pelos métodos corriqueiros e esta é uma dentre as inúmeras situações em que o formalismo lagrangeano mostra-se bastante útil.
* * * * *
Temas Relacionados:
Referências:
[1] - DIRAC, P.A.M. (1967): The Principles of Quantum Mechanics, fourth edition (revised), Oxford Science Publications, capítulo 1, item 1 (A necessidade para uma teoria quântica), pp 1-4. "A mecânica clássica foi desenvolvida continuamente desde o tempo de Newton e aplicada a um amplo espectro de sistemas dinâmicos, incluindo o campo eletromagnético em sua interação com a matéria."
[2] - NEWTON, I.: Opticks, fourth edition (1730), Dover Publications, New York, 1979, p. 402.
[3] - DIRAC, P.A.M. (1967), op. cit.
[4] - JOSÉ, J.V.; E.J. SALETAN (1998): Classical Dynamics – A contemporary approach, Cambridge University Press, Cambridge, UK, , p. 201.
[5] - DIRAC, P.A.M. (1967), op. cit.: "Não obstante, demonstrou-se ser possível montar um novo esquema, denominado mecânica quântica, mais adequado para a descrição de fenômenos na escala atômica e que tem se mostrado, em alguns aspectos, mais elegante e satisfatório do que o esquema clássico."
[6] - HERRERA, A. (1983), Verdade científica e beleza 1, Folha de São Paulo, 25/06/83, página de Educação (Ciência e Sociedade).
[7] - GRECO, A. (2001), Homens de Ciência, Conrad Livros, São Paulo, p.21.
[8] - BORN, M., P. AUGER, E. SCHRÖDINGER, W. HESENBERG (1969), Problemas de Física Moderna, Ed. Perspectiva, São Paulo, p. 46.
[9] - BROWN, H. (1983), A estranha natureza da realidade quântica, Ciência Hoje, vol. 2., n° . 7.
[10] - MESQUITA F° ., A. (2001), Sobre as origens da física moderna (editorial), Integração: VII(26):163-4.
[11] - EINSTEIN, A., L. INFELD (1980), A evolução da física, Zahar Edit., Rio de Janeiro.
[12] - LACEY,H.M. (1972): A linguagem do espaço e do tempo, Ed. Perspectiva S.A.
[13] - FERRAZ NETTO, L. (2000) Ampliador óptico de deformações, Feira de Ciências - Sala 06, Estática, experimento 26.
[14] - Para maiores esclarecimentos a respeito sugiro uma visita a: FERRAZ NETTO, L. (2000) Ação e Reação (modelo newtoniano 1), Feira de Ciências - Sala 17, sugestões didáticas, item 17_01.