Continuação da mensagem 11:

Como afirmei na mensagem 04, a Termodinâmica poderia ser chamada "Dinâmica das Transformações e/ou Interações entre os Sistemas". Sua generalidade ultrapassa os limites do estudo dos processos em que a temperatura ou o calor desempenham os papéis principais. Não obstante, o calor é fundamental para o estudo da dinâmica das interações entre sistemas e, de alguma forma, sente-se a sua importância até mesmo nos processos em que não há transferência de calor.

Até o momento temos visto transformações em gases e esta é talvez a maneira mais apropriada (ou pelo menos a mais simples) para se iniciar o estudo da termodinâmica. Nestes estudos iniciais, mesmo quando o modelo é diverso deste tradicional, o outro sistema é, via de regra, "o restante do Universo"; às vezes iniciamos o estudo através da conceituação de sistemas isolados mas em algum momento temos que evoluir para a consideração de um segundo sistema, sob pena de não entrarmos na termodinâmica propriamente dita. A interação entre dois sistemas de dimensões finitas não é tão trivial, levando-nos às vezes a situações paradoxais. O "restante do Universo", ou outro sistema qualquer de dimensões praticamente infinitas (tão grande quanto se queira) facilita algumas passagens, sem dúvida alguma conflitantes.

As propriedades que mais serão úteis, e a proporcionarem a axiomatização da teoria, referem-se obviamente a propriedades definidas para sistemas finitos; e é por isso que o enfoque principal deve se voltar não para o Universo em si, mas para o sistema finito e que, no caso escolhido, é um gás. É óbvio que de alguma forma percebemos algumas propriedades relativas ao sistema "infinito" acoplado ao estudo, porém retratam condições envoltas por um certo ar de mistério consequentes a algumas idealizações inferidas e que, sem aparentemente prejudicar o estudo e suas conclusões, passam por secundárias, sendo mal definidas e mal comentadas (as vezes até mesmo por serem mal conhecidas), gerando insatisfações. Os conceitos "ordem" e "seta do tempo", além de outros, situam-se neste terreno.

Estamos pois numa encruzilhada a nos apontar dois caminhos: ou avançamos em considerações relativas ao segundo sistema (no caso, o "restante do Universo"), ou seguimos a rota tradicional, a fixar a atenção no sistema mais simples. Como sei que os dois caminhos muito em breve convergirão, sei também que não perderemos nada se tomarmos o caminho mais longo, qual seja, o primeiro acima citado. Aliás, diria que ganha-se muito com isso. Em primeiro lugar, porque esta via nos mostra precocemente a irregularidade do terreno pelo qual teremos que passar; em segundo, porque é mais filosófica, chamando-nos a atenção para as raízes dos problemas que na sequência teremos que enfrentar; e em terceiro, porque satisfaz a nossa curiosidade de entender o porquê das analogias efetuadas. O segundo caminho é mais axiomático e tem a vantagem de nos levar rapidamente à caracterização da entropia e outras grandezas associadas. Satisfaz aqueles que gostam da matemática, ainda que nem sempre estes demonstrem gostar suficientemente da termodinâmica.

Aliás, tenho feito críticas, não à axiomatização mas, aos modernos modelos pedagógicos que valorizam estes caminhos mais curtos. Em decorrência do ensino moderno, não é raro encontrarmos físicos que sabem encontrar a solução para as integrais mais complicadas que possamos imaginar e, no entanto, não têm a mínima noção do que seja limite, um conceito que deveriam ter assimilado antes de efetuarem, por métodos matemáticos, suas primeiras integrações. Vez ou outra perdem-se em seus algoritmos e cometem erros incríveis, até mesmo a comprometer a exatidão de seus resultados matemáticos. Quando questionados a respeito, eles estranham nosso questionamento e "recitam" a definição de limite "aprendida" em seus primeiros anos de Cálculo e que, embora do ponto de vista conceitual diga tudo, do ponto de vista prático não diz absolutamente nada, a menos que saibamos efetivamente o que estamos dizendo e o porquê dos matemáticos terem escolhido palavras tão complexas para expressarem um conceito por demais simples.

Vamos então tomar o caminho mais longo. Tecerei algumas considerações a respeito e relacionadas à transformação mostrada na figura 1, agora com mais detalhes e reapresentada, a seguir, na figura 4.

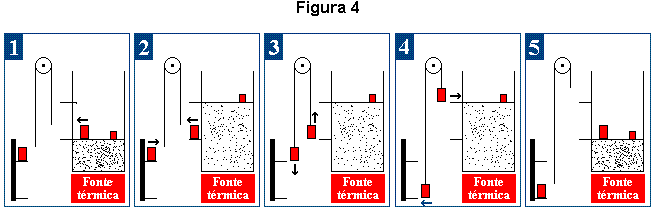
A figura 4 demonstra os processos então descritos como de "ida" (1 a 2) e de "volta" (4 a 5) além de considerar o que há de importante, para o caso, no "restante do Universo" e que em síntese são:

1. um sistema (polia) que permite a elevação da massa M;
2. uma fonte de calor;
3. uma sutil e desprezível, em termos de Universo, porém quase sempre presente, variação no espaço efetivamente ocupado pelos dois sistemas (no caso do gás, a traduzir-se por uma variação significativa em volume).

Estas considerações serão apresentadas na próxima mensagem e, tão logo quanto possível, retornaremos à trilha principal. Espero com isso poder dizer alguma coisa mais sobre temas semelhantes àqueles que tem "encucado" os que têm dado algum retorno às minhas postagens.

Continuação da mensagem 12:

Vamos inicialmente resumir as idealizações assumidas na transformação mostrada na figura 4 contida na mensagem anterior:

1) Deslocamentos laterais das massas entre o êmbolo ou a polia e os suportes de massa. Não havendo atrito nem limitação temporal para se atingir o objetivo, pode-se raciocinar em termos de forças infinitesimais e portanto nulas quando em número finito. Na prática chega-se ao valor nulo, para o dispêndio de energia, como condição limite (força tendendo a zero e duração do processo tendendo a infinito).

2) Deslocamentos verticais das massas na polia: valem as considerações observadas em 1, pensando-se ainda em ausência de resistência do ar (massas no vácuo). A diferença de massas para iniciar o movimento pode ser considerada como um infinitésimo (menos de um grão de areia) e o tempo também pode ser pensado como infinito (a termodinâmica, sob o ponto de vista teórico, não estuda a duração do processo, interessando apenas o "antes" e o "depois"). Na prática o processo nunca é ideal mas pode-se pensar num limite ou numa tendência a essa idealidade teórica. O fio que sustenta os pesos pode ser também considerado com massa desprezível sem prejuízos para a teoria decorrente (sua posição final diversa da inicial, nestas condições, não prejudica a teoria).

3) A fonte de calor é considerada suficientemente grande para que as trocas de calor que efetua com o sistema gás não alterem sua temperatura, a menos que dentro de limites desprezíveis. Assim, um transporte de calor em quantidade suficiente para provocar uma variação de temperatura razoável num sistema finito e de dimensões não muito grandes, não fará mais do que promover uma variação infinitesimal na temperatura da fonte, o que, para todos os efeitos, não se repercutirá em algo mensurável, nem com respeito a fonte, nem com respeito ao gás que está em equilíbrio térmico com a mesma.

4) Ao dizermos que as transformações são isotérmicas estamos assumindo a instantaneidade do equilíbrio gás-paredes-fonte. Por um lado poderíamos pensar no fator tempo e que, como assumido acima, pode ser desconsiderado em teoria. Por outro, estamos implicitamente assumindo, caso o equilíbrio não seja instantâneo, que qualquer retardo no processo, e por si só, não afete, de maneira mensurável, o processo como um todo. Ou seja, desde que o estado final esteja bem definido e com temperatura igual à inicial, o tempo que o calor leva para ir da fonte ao sistema ou vice-versa é irrelevante (e, consequentemente, o material a constituir as membranas fronteiriças, desde que permita o equilíbrio final, não tem interesse teórico, a menos que estivéssemos pensando em equipamentos tecnológicos, mas aí estaríamos falando em "teoria da prática", o que é outra coisa). Dito de outra forma, assim como assumimos ausência de atritos, massa desprezível do êmbolo, resistência do ar nula, etc., estamos aqui também assumindo a existência de uma membrana impermeável à matéria mas totalmente permeável ao calor que, por outro lado, espalha-se idealmente e instantaneamente por todo o sistema (qualquer desvio desta idealidade é aceito como algo a não interferir sobre os significados ou valores das propaladas propriedades do Universo).

5) Alguns autores chamam a atenção para a irreversibilidade no transporte espontâneo de calor entre uma fonte quente e uma fonte fria: pela utilização de infinitas fontes secundárias, imaginam modelos teóricos onde quantidades finitas de calor podem ser transportadas reversívelmente, a menos de um infinitésimo (a exemplo do mostrado para pequenas massas tendendo a zero), de sistemas quentes para sistemas frios. Digo isso porque se o equilíbrio não se der instantâneamente, como exposto acima, existirão, na realidade, e mesmo na transformação isotérmica, estados intermediários em que fonte e gás poderão estar em diferenças finitas de temperatura, e a irreversibilidade poderá não se restringir a efeitos medidos através de alturas de massas. Este efeito acaba sendo desprezado, juntamente com outros já comentados, por considerarmos o "antes" e o "depois" sem levar em conta o "durante".

6) Ainda que o volume do gás varie consideravelmente, quando pensamos no confronto gás-Universo, podemos sossegadamente afirmar que o volume do "restante do Universo" permanece praticamente constante. Isso não se traduz em problemas relevantes para a maioria dos estudos termodinâmicos, casos em que o segundo sistema, para efeitos práticos, é da ordem de grandeza do "restante do Universo". Deve-se aqui também observar outra condição que somente ocorre graças ao fato de o segundo sistema ("resto do Universo") poder ser aceito como com dimensões infinitas: Na expansão de um gás contra a atmosfera, a pressão do segundo sistema permanece sempre constante, a menos de infinitésimos. Não é impossível que ocorram variações finitas (temporárias e locais, ou seja, imediatamente acima do êmbolo) e que são deixadas de lado no modelo proposto e a considerar apenas o "antes" e o "depois". Como a pressão de oposição do sistema 2 relaciona-se ao trabalho exercido pelo sistema 1 sobre o sistema 2, e este trabalho é o que efetivamente é considerado ao se deduzir as fórmulas termodinâmicas, percebe-se aqui mais uma idealidade aceita, porém questionável.

No estudo de sistemas finitos e em confronto ou, mesmo, no caso do estudo de três sistemas, sendo dois finitos e sendo o terceiro sistema "o restante do universo", verificamos situações paradoxais a demonstrarem que, de alguma maneira, o modelo termodinâmico adotado parece conter algumas imperfeições de natureza lógica e, a primeira vista, irremediáveis. Aparentemente não há como aplicar esta termodinâmica, que via de regra "funciona", para algumas situações onde o segundo sistema reduz-se a proporções finitas; a menos que ele possa, para todos os efeitos práticos, ser considerado de proporções infinitas (e desta forma caímos no caso anterior, apenas reduzindo mentalmente, ou mesmo do ponto de vista prático, o que chamamos "resto do Universo"). Esses problemas via de regra surgem quando existe transferência de trabalho, do tipo que se acompanha de variação de volume, de um dos sistemas finitos para o outro, como é o caso mostrado na figura 5 abaixo. Com frequência diz-se tratar-se de um sistema único compartimentalizado (dois compartimentos, no caso).

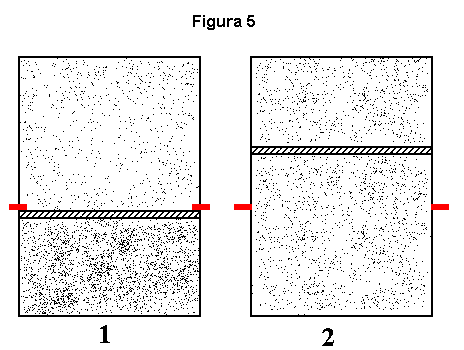
A figura 5 mostra um sistema de dois compartimentos com gases em condições iniciais diferentes. As possibilidades de estudo são:

1. Paredes do recipiente rígidas e adiabáticas, sem permitir trocas de energia com o exterior;
        a) êmbolo adiabático;
        b) embolo diatérmico.
2. Paredes do recipiente rígidas e diatérmicas, permitindo trocas de calor com o exterior.

Os casos 1a e 1b referem-se ao estudo de dois sistemas finitos e em confronto passível de transferência de trabalho de um para o outro; o caso 2 refere-se ao estudo de três sistemas, sendo dois finitos e sendo o terceiro "o restante do Universo", que pode ou não trocar trabalho com o conjunto, além de calor (imagine, por exemplo, um fio preso ao êmbolo e que, atravessando as paredes do recipiente por algum hipotético procedimento, e a não prejudicar o modelo, estivesse apto a elevar um peso exterior ao sistema de dois compartimentos. às custas de trabalho exercido pelo sistema compartimentalizado).

Na figura 5 o número 1 refere-se ao estado "inicial" e o número 2 ao estado "final" do conjunto. A massa m não é necessária pois no estado "inicial" ela foi substituída por uma presilha e o estado "final" retrata um equilíbrio de pressões. Para estados intermediários seriam necessárias massas m variáveis conforme o caso e presilhas outras em alturas diferentes e a brecarem o êmbolo. Tente verificar nesse exemplo o quanto as idealidades acima apresentadas ficam a nos dever consistência. A situação existe na prática, obviamente sem as idealidades imaginadas. Na prática o êmbolo atinge o equilíbrio; em teorias outras (mecânicas) o êmbolo, graças às idealidades aceitas, poderia oscilar eternamente pois não há atrito; por outro lado, sendo o êmbolo sem massa, a resistência é exercida sobre o gás e não propriamente sobre a massa do êmbolo. Não obstante, seguindo o método termodinâmico podemos desprezar tudo isso e raciocinar com o "antes" e o "depois", visto que, se o processo existe na prática, existe um "antes" e um "depois" e, para a termodinâmica, não interessa a evolução do processo. Perceberemos, no entanto, que isso nos levará a um paradoxo (ainda não descrito aqui), relacionado à conservação da energia (primeira lei). Bem, a dúvida está lançada, o "brinquedinho" está aí (figura 5) e as idealidades estão apontadas acima. Divirtam-se. Para os que dominam a primeira lei: Tentem localizar o paradoxo! Retornarei oportunamente a discutir este sistema à medida que avançarmos no estudo dos demais e que sujeitam-se ao modelo clássico. Qualquer comentário, sugestão ou dúvida, não deixem de relatar.

Observação 1: Descobri esse paradoxo em 1975 e o apresentei em seminário da disciplina de Termodinâmica Aplicada a Sistemas Biológicos, na Usp (Fisiologia). Até hoje não encontrei uma solução convincente, por mais que tenha procurado. Apresentei o mesmo em vários newsgroups nacionais e internacionais e o paradoxo persiste, sem solução. Apesar disso continuo a estudar termodinâmica, pois sinto que, dentro de determinadas condições, ela funciona e, onde ela, a meu ver, parece não funcionar, as teorias que pretenderam sucedê-la, sem sucesso até o momento, também não funcionam. De qualquer forma, levo dentro de mim a sábia mensagem de Mário Schenberg: "Quando uma coisa começa a se complicar muito, é sinal que é preciso simplificá-la". Como simplificar a termodinâmica se não abordarmos a raiz do problema?

Observação 2: Amanhã (12/12/99) farei um pequeno recesso com a finalidade de contabilizar o que de importante está faltando para que possa responder a contento as questões pendentes. Retornarei na segunda-feita. Não obstante, estarei "ligado" na Internet e a disposição para responder pequenas dúvidas relacionadas ou não às mensagens já postadas.

Vamos raciocinar agora em termos do trabalho W realizado pelo sistema 1 (gás, no caso) nos vários processos descritos ou imaginados nas mensagens anteriores (com N variando de 1 a infinito, sendo N o número de etapas). Para N = 1 (figura 1) já vimos que o único trabalho W₁ é aquele relativo ao levantamento da massa m da altura h (W₁ = mgh). Para N = 3 (figura 2), além do gás realizar este trabalho mgh, pois a massa m também é elevada da mesma altura (vide estado final 4), verifica-se que frações da massa M (M/3 no caso) foram elevadas de alturas várias (entre 0 e h). Se chamarmos as possíveis alturas dos embolos por h₀, h₁, h₂ e h₃, correspondendo respectivamente aos estados 1, 2, 3 e 4 mostrados na figura 2, verificando-se ainda que h₀ = 0 e h₃ = h, e observando-se as massas como dispostas no suporte, em 4, concluiremos que o trabalho total realizado pelo gás iguala-se a:

W₃ = (M/3)gh₀ + (M/3)gh₁ + (M/3)gh₂ + mgh₃ =

       = (M/3)gh₁ + (M/3)gh₂ + mgh =

       = (M/3)g(h₁ + h₂) + W₁.

Ou seja, W₁ é menor do que W₃, como seria de se esperar, e por um valor que pode ser calculado "experimentalmente". E não é difícil observar, mesmo em teoria, que para outros valores de N chegaríamos à conclusão que:

W₁ < W₂ < W₃ < W₄ < ... < W₈₀ < ... < W_infinito = W_max

(W_max = máximo trabalho que poderia ser extraído deste sistema-gás, numa transformação isotérmica entre os estados definidos na figura 1 como inicial e final). Mas, como vimos, N = infinito corresponde ao que chamamos processo reversível a menos de um infinitésimo (que, para todos os efeitos, identificamos como sendo o processo reversível propriamente dito).

Entendido o processo do ponto de vista analítico, é possível que pairem dúvidas a respeito da afirmação feita no parágrafo anterior: "não é difícil observar, mesmo em teoria, que...". Esta passagem não é trivial, posto que os diversos valores de h_i não estão ainda definidos. E, com efeito, não iremos defini-los. Lembrem-se de que a termodinâmica é um capítulo da física e não da matemática. A física apóia-se na experimentação e mesmo quando lança mão de processos imaginários, sejam idealizações, sejam experiências de pensamento, deve ater-se a interpretar o que efetivamente ocorre na natureza (fenômenos naturais). Para isso observa-se que muitas grandezas desempenham papéis mais claros do que outras e, para o nosso caso, ao caminharmos nessa direção, podemos nos livrar de ter que interpretar todos os matematicamente possíveis valores para os diversos h_i's. É chegada a hora, então, de lançarmos mão das demais propriedades dos gases: p, V e T. Mesmo porque, de alguma forma verificaremos que os h_i's relacionam-se com os respectivos volumes V_i's do gás observados na etapa correspondente da expansão. Qual seria essa relação?

Mudemos um pouco o enfoque relativo às variáveis do problema.

1. Digamos que m seja uma massa "variável" e numericamente igual, "a cada instante", à "massa total que permanece em cima do êmbolo". Seu valor, ao final da transformação, coincidirá com aquele que até agora vínhamos adotando para m (os demais valores de m não estavam definidos desta maneira). Em particular, no início da transformação m será, agora, igual à soma anterior M + m. Estamos homogeneizando as grandezas, com a finalidade de facilitar as expressões que se seguem. Neste caso, m será sempre a "massa que sobra" e cada etapa poderá ser pensada, a esse respeito, como idêntica ao processo como um todo.
    
2. Chamemos a diferença em alturas entre um estado e outro de Δh, a corresponder às diferenças entre dois valores h_i consecutivos. Nestas condições, o trabalho realizado pelo gás ao passar de um estado para o seguinte será igual a W = mgΔh, sendo m, medido ao final de cada etapa, a massa que foi efetivamente elevada pelo gás durante a etapa correspondente. O número de etapas continuará sendo chamado por N.
    
3. Pensemos agora na variação do volume do gás durante cada etapa. Digamos que essa variação tenha sido ΔV = V_final - V_inicial = V_f - V_i (em que final e inicial correspondem à etapa do processo e não ao processo todo). À medida que o volume variou de ΔV, a altura variou de Δh e tal que ΔV seja igual a:
                                                   ΔV = AΔh,
   sendo A a área do êmbolo.

Podemos agora exprimir o trabalho W em termos de variação de volume. Ou seja, o trabalho W = mgΔh, realizado pelo gás ao passar de uma etapa da transformação para a seguinte, pode ser expresso por

W = mgΔV/A.

Mas mg é a força peso (P = mg) exercida sobre o gás pela massa m no estado final desta etapa e esta força peso exerce uma pressão p_op = P/A (p_op = pressão de oposição) sobre o êmbolo e que está momentaneamente em equilíbrio com a pressão do gás, ou seja:

pressão do gás no estado final da etapa = p = p_op = mg/A.

Consequentemente, podemos escrever: W = pΔV. É importante lembrar que p, usado nesta fórmula, está substituindo a pressão de oposição p_op exercida pelo conjunto massa m e êmbolo de área A, a qual iguala-se à pressão do gás no modelo apresentado. Esta igualdade nem sempre se verifica. Alguns autores gostam de enfatizar esta restrição escrevendo a fórmula como W = p_opΔV, o que sem dúvida alguma é mais correto.

Conseguimos então relacionar o trabalho de levantamento de massas realizado pelo gás entre um estado e outro de um processo irreversível através das propriedades do gás p e V. Embora os exemplos assinalados refiram-se a transformações isotérmicas, esta restrição não foi utilizada e a equação vale também para outras condições como, por exemplo, condições adiabáticas (sem trocas de calor com o ambiente). Não é demais lembrar que a pressão que entra na expressão de trabalhos que contenham ΔV (e portanto, transformações finitas que podem ou não ser infinitesimais) é a pressão final da etapa correspondente. Em dúvida usem W = p_fΔV, reservando p para trabalhos infinitesimais W = pδV (O símbolo "δ" ao invés de "d" é utilizado para que fique explícito que W não é uma diferencial exata; alguns utilizam, com a mesma finalidade um "d" ou "del" cortados).

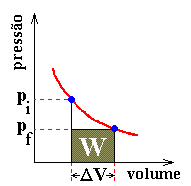Com esses dados, podemos evoluir para as representações gráficas, o que facilitará bastante o entendimento do processo. A figura 6 representa uma das etapas da transformação em que p_f = pressão final, p_i = pressão inicial e ΔV = variação de volume entre o estado inicial e o final. Trata-se de um gráfico pV (pressão × volume) sendo que a linha vermelha representa um possível caminho dentre aqueles que a experiência demonstra ocorrer na prática. O trabalho W, realizado pelo gás durante esta etapa do processo, está representado no gráfico como sendo numericamente igual à área p_fΔV, desde que as escalas do gráfico tenham sido escolhidas convenientemente. Normalmente o estudo é efetuado utilizando-se caminhos isotérmicos e/ou adiabáticos. Como veremos, é sempre possível passar-se de um estado qualquer para outro seguindo-se exclusivamente vias isotérmicas e adiabáticas, e isto facilita sobremaneira o estudo.

Observação: Algumas letras gregas somente são visualizadas em computadores que possuem a fonte Symbol que normalmente acompanha o Windows [caso contrário é possível que o Δ (delta maiúsculo) apareça como D].

Continuação da mensagem 14:

A figura 7 mostra gráficos pV para transformações em várias etapas (N = 1, N = 2, N = 3 e N = infinito) e que seguem um mesmo caminho (em vermelho). As condições finais de cada etapa são de equilíbrio entre p_op (pressão de oposição) e p_f (pressão final, ou simplesmente p). O equilíbrio ocorre, como vimos, graças à massa m que persiste em cima do êmbolo.

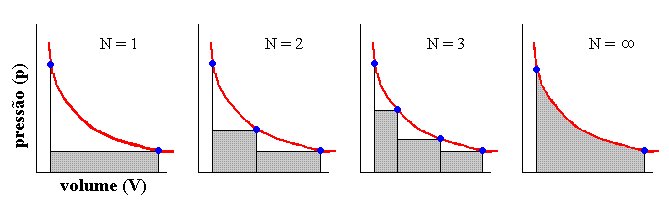
Figura 7

Não é difícil perceber que o trabalho total depende do número de etapas e, agora sim, visualizamos facilmente no gráfico o afirmado anteriormente: W1 < W2 < W3 < W4 < ... < W80 < ... < W_infinito = W_max. Justifica-se então a expressão "trabalho máximo" (W_max) utilizada para processos reversíveis (N = infinito). Fixados os estados inicial e final e conhecido o caminho a ser seguido por um gás ao sofrer uma transformação de estado, podemos dizer que "o máximo de trabalho que pode ser extraído desse gás durante o processo e a ser convertido em levantamento de massas dá-se quando a transformação é reversível, ou W_max = W_rev. A transformação (ou o caminho) poderá ser isotérmica, adiabática ou qualquer outra bem definida e que possa ser reproduzida experimentalmente. Obviamente, e como explícito, W_max é uma função de caminho ou de via. Em especial, se a transformação for a volume constante (isocórica) todos os W serão nulos (tanto os irrev quanto o rev).

O fato de W_max ou W_rev ser uma "função de caminho" dificulta a sua utilização na caracterização de uma propriedade de estado do sistema gás, a menos que aceitemos determinadas restrições (vide nota de rodapé). Poderíamos pensar em restringir a via. Neste caso, se escolhermos uma via isotérmica, poderemos dizer que o gás, cujo comportamento restringe-se a esta via, possui uma propriedade Ø de alguma forma relacionada ao W_max acima descrito. Por exemplo, o gás restrito ao equilíbrio térmico com uma fonte de calor de temperatura fixa, teria uma propriedade Ø, chamada "função trabalho máximo", dada pela expressão ΔØ = Ø₂ - Ø₁ = - W_max. Ou seja, ao passar de um estado para outro, a temperatura constante, o gás teria sua propriedade Ø reduzida exatamente do valor do trabalho que produziria caso a transformação fosse reversível. ΔØ retrataria a quantidade de "energia disponível pelo gás para a execução de trabalho" entre um estado e o outro. A primeira vista esta função é de pouco interesse, visto somente ser útil para situações em que, entre um estado e outro, o gás permanece em equilíbrio térmico com a fonte considerada. Como adequar esta função ao estudo efetuado em condições outras, ou mesmo em equilíbrios outros, com outras fontes ou temperaturas?

Guardem essa idéia por enquanto. Deixá-los-ei com a figura 8 onde são apresentados alguns caminhos ou vias de transformação a serem seguidos por um determinado gás.

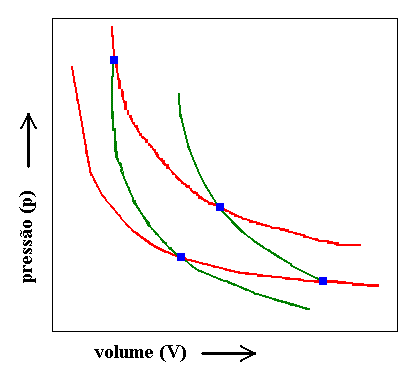
Figura 8

Em vermelho estão vias isotérmicas e em verde vias adiabáticas, e é importante notar o relacionamento entre estas vias. Se definíssemos uma propriedade Ø através de uma restrição do comportamento do gás a um equilíbrio térmico com a fonte quente (isotérmica superior) e, assim sendo, relacionada à "função trabalho máximo" observada em transformações restritas a esta via, pergunto: O que precisaríamos fazer para que a função Ø pudesse ser expandida para as demais linhas, representando assim uma propriedade do gás em toda a sua plenitude? Na outra isotérmica (inferior) devemos esperar o mesmo relacionamento entre Ø e W_max mas... Como chegar ao seu valor relativo aos estados definidos na isoterma superior? Dito de outra maneira: Se dermos um valor Ø₁, correspondente a um estado 1 do intervalo mostrado na isoterma superior, poderemos, pela observação de W_max, calcular todos os demais Ø_i nesta isoterma. Pergunto então: Como calcular pelo menos um dentre os infinitos Ø_j da isoterma inferior, em função de Ø₁? Como variaria a propriedade Ø numa adiabática? Essa variação teria alguma relação com o W_rev aí observado?

Lembrem-se:

1. Estamos propondo a definição de uma propriedade Ø tal que ΔØ venha a representar a quantidade de "energia disponível pelo gás para a execução de trabalho" entre um estado e o outro situado numa mesma isoterma. Não estamos afirmando que ΔØ seja sempre igual a - W_max, embora isso deva ocorrer nas demais isotermas, caso seja possível definir Ø.
    
2. Uma propriedade de estado deve apresentar valores, em cada estado, que não dependam da maneira como o estado foi atingido.
    
3. Numa adiabática a quantidade de calor trocada pelo gás e o meio ambiente é igual a zero.
    
4. Ainda não falamos nada sobre temperatura, a não ser sobre a possibilidade do gás estar em equilíbrio com uma fonte. O que é temperatura? Não poderíamos estar aqui precisando também definir a temperatura, juntamente com a definição de Ø? Obviamente, para tal, deveremos lançar mão de outros princípios mas... Qual é o princípio que permite a definição de temperatura? Não é o princípio do equilíbrio térmico? E não estamos trabalhando com restrições implicitamente relacionadas a esse princípio (equilíbrio gás-fonte de calor)?
    
5. Por falar em outro princípio, que dizer da primeira lei (ΔE = Q - W)? Estou usando aqui a seguinte convenção: Q = calor "recebido" pelo sistema; W = trabalho "efetuado" pelo sistema; e ΔE = variação da energia interna do sistema. Como "Q Û recebido" e "W Û efetuado", entende-se a diferença de sinais. Esta é a convenção mais usada, mas alguns autores usam +W (trabalho recebido) no lugar de -W. A lei é a mesma, muda apenas a simbologia.

Retornarei com novas "encucações" após o dia 16. Sinto que as dúvidas são poucas. Ou eu estou sendo muito claro (pouco provável), ou estou sendo por demais confuso, ou então o tema não tem despertado muito interesse. De qualquer forma, lembro que o meu arsenal está se esgotando. Ainda bem que estamos quase chegando na entropia, o que representará o desfecho das minhas apresentações, após é claro, responder a algumas dúvidas pendentes apontadas pelo André bem como elucidar o paradoxo citado em mensagem anterior. Não pretendo, pelo menos nesta empreitada, dissecar as relações de Maxwell da termodinâmica, pois para isso teria que rever amplamente meus conhecimentos a respeito (até aqui tenho improvisado às custas de conhecimentos assimilados no passado).

Nota: Ser "função de caminho" é condição necessária, porém não suficiente, a ser apresentada por uma função de estado. Como W_max apresenta a condição necessária assinalada, precisamos conservar esta característica ao "construirmos" a propriedade derivada. Às vezes é mais fácil trabalhar com funções que não apresentam esta característica (a menos que já sejam funções de estado) e daí a "dificuldade" apontada.

Continuação da mensagem 15:

Construtos de Alto Nível

Dentre as várias propriedades de estado estudadas pela termodinâmica, algumas costumam ser referidas como "construtos de alto nível". Os exemplos típicos são energia interna E (alguns livros usam a notação U) e entropia S. São "construtos" no sentido que, de alguma forma, foram "construídas" afim de que pudéssemos traduzir, em linguagem matemática, o conteúdo de determinado(s) princípio(s). São de "alto nível" devido a resultarem de uma construção laboriosa, não sendo autoevidentes por si só, ao contrário de outras como pressão, volume e temperatura.

Mostraremos a seguir como chegar a uma propriedade de estado deste tipo a partir da "função trabalho máximo" descrita na mensagem 15. Como vimos, W_rev é uma função de caminho, condição esta que é "necessária porém não suficiente" para que seja uma função de estado. E, com efeito, não é, pois se calcularmos ΔØ = Ø₂ - Ø₁ (supostamente = W_rev) partindo-se de um estado qualquer, dentre aqueles representados na figura 8 por um dos pontos azuis, retornarmos a esse mesmo ponto após percorrermos duas isotérmicas e duas adiabáticas, e já que os pontos 2 e 1 coincidem, deveríamos ter, ΔØ = 0, o que significaria dizer Ø₂ - Ø₁ = 0. Mas se ΔØ = W_rev, ao efetuarmos o cálculo graficamente para todo o ciclo (da maneira mostrada na mensagem anterior) chegaremos à conclusão que ΔØ será numericamente igual a área do gráfico pV envolvida pelo ciclo e, portanto, diferente de zero. Logo, se quisermos aproveitar algumas das características da função Ø e com isso construir uma propriedade termodinâmica, devemos dotar Ø de algumas outras características; e daí a dificuldade apontada quando disse: "o fato de W_rev ser uma função de caminho dificulta a sua utilização na caracterização de uma propriedade de estado do sistema" (mensagem 15, terceiro parágrafo).

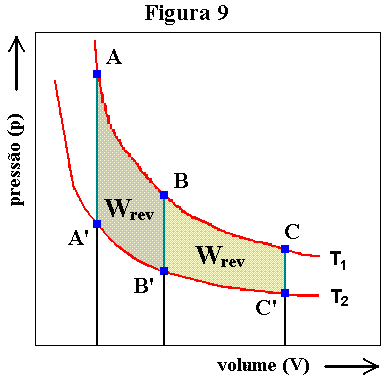Para simplificar a complexidade, vamos pensar no ciclo ABB'A'A representado na figura 9 inscrito em duas isotérmicas (T = constante) e duas isocóricas (V = constante). Digo que tal escolha simplifica o estudo posto que em transformações a volume constante o trabalho de levantamento de massas é igual a zero, seja a transformação reversível ou não e, portanto, W_rev = 0 no trecho considerado.

Vamos agora definir a propriedade Ø tal que entre quaisquer dois estados de uma mesma isoterma tenhamos ΔØ = C_fW_rev, sendo C_f (constante da fonte) uma propriedade relacionada à fonte de calor, ou seja, para uma mesma fonte teremos um mesmo C_f. Na isotérmica superior a variação de Ø entre A e B será dada por ΔØ_BA = C_f1W_revAB. Na isocórica que se segue (de B a B') temos ΔØ_B'B = Integral de B a B' de C_fδWrev = 0, com C_f = f(T) e W_rev = 0 durante toda a integração. Uma transformação isocórica "reversível" deve ser pensada como transformações infinitesimais a volume constante em que o gás equilibra-se sequencialmente com infinitas fontes com temperaturas que, no caso, variam de T₁ a T₂. Desta forma, C_f = f(T) deve variar de C_f1 a C_f2 à medida que o sistema caminha do estado B para o estado B'. Na isotérmica inferior devemos ter ΔØ_A'B' = C_f2W_revB'A'. E na isocórica restante, a fechar o ciclo, temos: ΔØ_AA' = Integral de A' a A de C_fδW_revA'A = 0 por motivos análogos ao já comentado para o trecho BB'. É interessante notar que o que estamos chamando propriedade relacionada à fonte de calor, C_f, poderia também ser pensado como propriedade relacionada à temperatura T da fonte ou do gás em equilíbrio com a fonte no estado considerado.

Como calcular C_f? Ora, para que Ø seja uma propriedade de estado devemos ter ΔØ_ABB'A'A = 0 e não é difícil concluir que devemos ter C_f1W_revAB = - C_f2W_revB'A'. Como já sabemos calcular (pelo menos graficamente) os vários W_rev, a relação C_f2/C_f1 está definida, sendo igual a -W_revAB/W_revB'A'. Definindo um C_f qualquer, teremos definido todos os demais C_f's. Será?

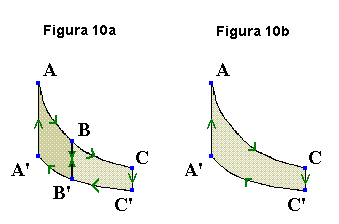Para que não pairem dúvidas pensemos no outro ciclo apresentado na figura 9, qual seja, BCC'B'B. O esquema está reproduzido na figura 10a, agora com flechas a indicarem as transformações. Temos então:

Transformação ABB'A'A:

ΔØ_BA = C_f1W_revAB

ΔØ_A'B' = C_f2W_revB'A'

e, como vimos:

C_f1W_revAB + C_f2W_revB'A' = 0                (eq 1)

Transformação BCC'B'B:

ΔØ_CB = C_f1W_revBC

ΔØ_B'C' = C_f2W_revC'B'

Por motivos idênticos deveríamos ter:

C_f1W_revBC + C_f2W_revC'B' = 0                (eq 2)

Estamos supondo que os C_f's podem ser os mesmos definidos para o caso anterior. Somando as equações 1 e 2 (eq 1 e eq 2) e manuseando-as convenientemente, temos:

C_f1[W_revAB + W_revBC] + C_f2[W_revC'B' + W_revB'A'] = 0

ou

C_f1W_revAC + C_f2W_revC'A' = 0.                (eq 3)

Mas a equação 3 seria a equação esperada para o ciclo ACC'A'A mostrado na figura 10b. Ou seja, a suposição de que pudéssemos utilizar os mesmos valores para C_f = f(T) na equação 1 e na equação 2 levou-nos a concluir ser esta condição também válida para a transformação ACC'A'A (eq 3). Ou seja, a matemática utilizada compatibiliza-se com os conceitos termodinâmicos implícitos na interpretação do gráfico (em especial a relação trabalho-área). Logo, tudo indica que estamos no caminho certo. Mas, onde nos levará esse caminho? Bem, até o momento conceituamos uma grandeza ou propriedade termodinâmica Ø. Mas, que dizer de C_f?

Para o entendimento do que se segue estou pressupondo que o leitor tenha conhecimento de rudimentos de Cálculo Integral. Se não tiver será suficiente que capte a conclusão a respeito de C_f e prossiga a partir daí.

Pensemos num gás ideal submetido à transformação cíclica representada na figura 10b. O trabalho reversível na etapa AC poderá ser calculado como:

W_revAC = pdV = nRT₁dV/V = nRT₁dV/V

ou

W_revAC = nRT₁ ln [V(C) - V(A)]                (eq 4)

em que p = nRT/V (gás ideal) com T = T₁ (temperatura da fonte quente). O mesmo cálculo realizado para o trabalho reversível na transformação C'A' nos fornece:

W_revC'A' = nRT₂ ln [V(A') - V(C'] = -W_revA'C'

ou, o que é o mesmo,

W_revA'C' = nRT₂ ln [V(C') - V(A')]                (eq 5)

Mas V(C) = V(C') e V(A) = V(A'). Consequentemente, de eq 4 e eq 5:

W_revAC/T₁ = W_revA'C'/T₂                (eq 6)

Pensando em termos de ΔØ, e pelo que já vimos, temos:

ΔØ_CA = ΔØ_C'A',

ou

C_f1W_revAC = C_f2W_revA'C'                (eq 7)

Logo, pela comparação das equações 6 e 7, conclui-se que um possível candidato a C_f = f(T) nada mais é do que 1/T, o inverso da temperatura absoluta. Aliás, é graças à propriedade utilizada nos cálculos efetuados acima (para o gás ideal) que utiliza-se, em termologia, o termômetro de gás para a definição do zero absoluto de temperatura. Em termodinâmica partimos do fato de que a escala absoluta ainda não está totalmente definida. Utilizamos então a propriedade acima estudada, e inerente à variável C_f (uma propriedade da fonte) para definir a escala termodinâmica de temperatura como aquela que satisfaz a condição T = 1/C_f.

Chegamos então à expressão de definição de Ø: Ø é uma propriedade termodinâmica de estado tal que entre um estado "i" e um estado "f" tenhamos

ΔØ = Ø_f - Ø_i = δW_rev/T

Se a transformação for isotérmica teremos

ΔØ = Ø_f - Ø_i = W_rev(i,f)/T.

A propriedade Ø, além de seu alto valor didático para o entendimento de outras variáveis termodinâmicas, tem pouca importância teórico-prática. Não obstante, graças a Ø podemos rapidamente "construir" grandezas outras de grande valor como a energia livre A de Helmholtz e a entropia. É o que faremos em nosso próximo Net-encontro que se dará, provavelmente, em 18/12/99. Até lá.

Continuação da mensagem 16:

Energia Livre "A" de Helmholtz

A energia livre "A" de Helmholtz pode ser definida pela expressão:

A = - TØ                (eq 1)

estando Ø definido através de ΔØ, na mensagem 16 de 16/12/99, como

ΔØ(f,i) = δW_rev/T ,                (eq 2)

em que "f" e "i" são índices a corresponderem respectivamente aos estados final e inicial da transformação considerada.

Observação: Não confundir a "energia livre A de Helmholtz" com a "energia livre G de Gibbs", também estudada em termodinâmica.

Partindo da equação 1 (eq 1) concluímos que, para uma transformação infinitesimal qualquer, é válida a expressão

dA = - d(TØ) = - TdØ - ØdT                (eq 3)

e, portanto,

ΔA(f,i) = - TdØ - ØdT.                (eq 4)

Não é difícil concluir, das equações 1 a 4, que ΔA é, via de regra, diferente de -TΔØ. Como exceção à regra temos que, para transformações isotérmicas (T = constante) chegamos a:

T = constante:                ΔA(f,i) = -TdØ = - TΔØ(f,i) = - W_rev(i,f)

Como vimos, nas transformações isocóricas (V = constante), Ø permanece constante pois W_rev = 0 durante todo o processo. Neste caso, temos:

V = constante:                ΔA(f,i) = -ØdT = - ØΔT(f,i) = f(V)ΔT

onde realçamos o fato de Ø ser uma função de volume através de Ø = f(V).

A energia livre "A" de Helmholtz tem a dimensão de energia; tanto assim é que, em processos isotérmicos, como vimos acima, sua variação ΔA iguala-se, com sinal trocado, a W_rev. Poderíamos dizer que o seu valor "A", num estado qualquer, relaciona-se intimamente com a "energia disponível pelo sistema para a realização de trabalho", decorrendo daí sua denominação "energia livre". Este relacionamento torna-se literalmente verdadeiro na expansão isotérmica, quando temos:

ΔA = - W_rev = - W_max                [T = constante]

O sinal de menos, como vimos, resulta da convenção aqui adotada para o significado de W (trabalho fornecido pelo sistema durante o processo e, portanto, se W for positivo, isto deverá se refletir numa diminuição não somente de "A" mas também da energia interna E do sistema).

Ora, se podemos pensar numa "energia disponível", a igualar-se a "A", que dizer do restante da energia interna "E" do sistema? Haveria uma "energia não disponível"? Ao que tudo indica, a resposta é positiva e esta "energia não disponível", para a realização de trabalho, retrata o caráter "caótico" ou "desordenado" do sistema. Como se vê, estamos muito próximos de compreender o significado de "desordem de um sistema". Percebam então que, procurando atender à dúvida inicial do André, percorri um caminho a nos levar à "necessidade" de definir uma grandeza, a que daremos o nome de entropia, com a finalidade precípua de expressarmos este tipo desordem. E esta grandeza é a mesma entropia que chega a ser definida, por caminhos outros, nos livros didáticos relativos ao tema.

Entropia

Pensemos na energia interna "E" de um sistema termodinâmico como que constituída por duas frações. 1) Uma fração "A", disponível para a realização de trabalho isotérmico, a traduzir-se num ΔA = -W_rev, e portanto já nossa conhecida; e 2) uma fração "X" não disponível para a realização de trabalho isotérmico e que, graças à primeira lei da termodinâmica, bem como da nossa pretensão em igualar "E" a "A + X", deverá traduzir-se num ΔX = Q_rev (pois, pela primeira lei, ΔE = Q - W = Q_rev - W_rev, válida para qualquer transformação).

Poderíamos pensar em definir a entropia igualando-a a "X". Mas isso não acrescentaria praticamente nada de útil, tanto do ponto de vista físico quanto matemático, ao nosso estudo. Quando muito, chamaria a atenção para algo que já possuímos, sendo suficiente subtrair "A" de "E". Pensemos então no nosso arsenal físico-teórico e que se traduz na observação de transformações em sistemas e na mensuração de grandezas relacionadas aos agentes causais imediatos dessas transformações, quais sejam, calor e trabalho, formas de energia em trânsito e que atravessam as paredes do recipiente que contém o sistema.

Ao estudarmos a energia livre "A", percebemos que ela "distingue-se", ou mostra evidências relativas a seu caráter termodinâmico, em duas condições especiais: 1) transformações isotérmicas, caso em que sua variação iguala-se, com sinal contrário, ao trabalho reversível cedido pelo sistema; e 2) transformações isocóricas, na qual o sistema não realiza trabalho de levantamento de massas. Percebemos ainda que para chegarmos à definição de "A", passamos por uma grandeza "Ø", de pouco interesse prático porém, e como visto, de elevado valor pedagógico (rigorosamente falando, "Ø" seria uma maneira atípica de expressarmos o volume do sistema). Existe, portanto, um par de grandezas (A, Ø) relacionadas ao W_rev e tal que A = ØT. Não seria de se esperar uma simetria entre calor e trabalho, a ponto de pensarmos num par de grandezas (X, S) relacionadas ao Q_rev e tal que X = ST? Pois essa simetria existe. E, ao contrário do "X" que, como dissemos acima, não acrescenta nada de útil que não possa ser obtido através de "E" e "A" já definidos, a grandeza "S" tem um potencial imenso de informações, a ponto de ser considerada, ao lado da energia, uma das duas mais importantes propriedades termodinâmicas de estado. Podemos então definir a entropia através da expressão

E = A + TS

ou

S = (E - A)/T.

Assim como para o perfeito entendimento da dupla (A, Ø), enfatizamos dois tipos de transformações, quais sejam, isotérmica (T = constante) e isocórica (Ø = constante), é de se esperar que no estudo da dupla (X, S) as transformações isotérmicas (T = constante) e adiabática (S = constante), representadas na figura 8, venham a desempenhar significados a facilitar a compreensão da entropia. E isto realmente ocorre.

Missão cumprida, retornarei nos próximos dias com novas mensagens no sentido de complementar alguma coisa relativa ao tema e/ou chamar a atenção para possíveis falácias interpretativas que tenha cometido, bem como para responder às questões que ficaram pendentes. Enquanto isso, ficarei à disposição para os esclarecimentos que se fizerem necessários.

 
Ü    Índice do Diálogo
Próximas Mensagens    Þ

DHTML Menu By Milonic JavaScript