Olá Pessoal,

Essa lista anda meio devagar né... Mas, felizmente, eu estou com uma dúvida gigantesca a respeito dessa tal de Entropia...

• Como podemos organizar o universo desorganizando o nosso sistema??
• O que é entropia finalmente???
• Por que os físicos gostam tanto de conceitos tão malucos???
• Entropia = Desordem???
• A entropia é infinita??

Por favor pessoal, cooperem com este simples aluno de engenharia (Eu).

OBS: A prova de Termodinâmica já passou, eu fiz mas não entendi nada....

Ávido por respostas,

André Camello

Olá André

André: Essa lista anda meio devagar né...

"Tirante" o Edu, que de vez em quando indica alguns sites interessantes, os demais "andam de farol baixo".

André: Mas, felizmente, eu estou com uma dúvida gigantesca a respeito dessa tal de Entropia... Como podemos organizar o universo desorganizando o nosso sistema?? O que é entropia finalmente??? Por que os fisicos gostam tanto de conceitos tão malucos??? Entropia = Desordem??? A entropia é infinita??

Pô! Pelo visto você está propondo tirar o atraso da lista Vamos com calma. Vou tentar responder a alguma coisa e se você der algum retorno tentarei, homeopaticamente, nivelar nossos conhecimentos e, com isto, tentar diminuir a entropia do sistema. Ou será que ela aumenta? (o sistema somos nós e os demais elementos da lista). Embora meus conhecimentos sejam limitados, pelo visto a tarefa irá demorar bastante. Quem sabe alguém possa contribuir e, desta forma, nivelaremos nossos conhecimentos numa altura maior.

André: Por favor pessoal, cooperem com este simples aluno de engenharia (Eu).

Ainda bem que você é da área de exatas, caso contrário a tarefa seria redobrada.

André: OBS: A prova de Termodinâmica já passou, eu fiz mas não entendi nada....

Então você está na média.

André: Ávido por respostas,

Pois então vamos lá. Vou começar com a antepenúltima questão:

André: Por que os fisicos gostam tanto de conceitos tao malucos?

Gosto não se discute. Realmente os físicos são assim mas, apesar disso, noto que a maioria dos físicos que andam por aí (pelo menos os da atualidade) não gostam muito da termodinâmica. Aceitam-na conquanto fundamental em inúmeras condições e como ponto de partida para muitos dos conceitos malucos a que você se refere, porém não a valorizam convenientemente. Por sinal, em termos de maluquice a física quântica dá de dez a zero na termodinâmica e a relatividade chega a uns sete ou oito a zero. Quem valoriza devidamente a termodinâmica são os físico-químicos e, em menor grau, os bioquímicos ou biofísicos. Talvez os físicos não gostem muito da termodinâmica pelo fato de seus conceitos não serem suficientemente malucos. Ou então porque, conforme assinalou Schemberg [1984, Pensando a Física, Ed. Brasiliense, São Paulo], não conseguiram compactuar a termodinâmica com suas maluquices do dia-a-dia. Schemberg afirma: "Há uma coisa sobre a qual a mecânica quântica não lançou luz alguma: o segundo princípio da termodinâmica". E após algumas considerações, conclui: "Há, aí, alguma coisa de fundamental que ainda não compreendemos. Quando uma coisa começa a se complicar muito, é sinal de que é preciso simplificá-la." Ora, mas qual é o físico, além de Mario Schemberg (falecido, por sinal), que quer simplificar alguma coisa? Como você mesmo disse, eles "gostam tanto de conceitos tão malucos".

André: Entropia = Desordem?

Não, embora possamos dizer, com ressalvas, que a entropia "mede" a desordem de um sistema. Seria então a medida da desordem e não a desordem em si. Convém então caracterizar o significado adotado no caso para as palavras "ordem" e "desordem". Vou reproduzir aqui o trecho de um texto que escrevi em 1983. Neste texto vou além da termodinâmica mas, de qualquer forma, se você não concordar com os demais conceitos e/ou conclusões, pelo menos poderá entender o significado da referida desordem.

---

Sistemas em Evolução: [Extraído de "Os átomos também amam", cap. 12 - A ciência autêntica, 1983, pp. 97-100, Ed. da Faculdade (hoje Universidade) São Judas Tadeu]

O leitor já deve ter saboreado um bom vinho; e já notou que quanto mais velho melhor; ou seja, o vinho modifica-se no decorrer do tempo. Isto pode se dever a dois fatores: ou o isolamento não é perfeito, ou o vinho modifica-se expontaneamente, pois não está em equilíbrio; ou, o que é mais provável, ambos. Se o vinho estivesse em equilíbrio e "bem" isolado, os séculos passariam e ele seria sempre igual.

Sistemas isolados e em equilíbrio são hipotéticos. Portanto, os princípios até aqui relacionados (nos ítens anteriores) são condições limites, ideais. Mas válidas, permitindo que a tecnologia se desenvolva sobre leis deles derivadas. E é comum a admissão de pelo menos um sistema isolado perfeito: o Universo. E o mesmo está em evolução. E ao que parece, é como o vinho: quanto mais velho melhor. A humanidade também está em evolução e...; é melhor não falar.

Obedecerá a evolução do Universo a algum princípio? Aparentemente sim. Dizem os físicos e os físico-químicos que o Universo caminha para um estado de entropia máxima, ou seja, um máximo de desorganização. Dizem os biólogos evolucionistas, por outro lado, que o Universo caminha para um estado de máxima complexidade: anteontem existiam apenas as bactérias; ontem os invertebrados; e hoje o ser mais complicado que já se conheceu. Esta complexidade denota um grau de organização não muito coerente com a idéia de aumento da entropia. Haveria por acaso dois princípios? Um relacionado à matéria inanimada e outro à matéria viva? Mas a matéria inanimada torna-se animada e vice-versa! Não há como distinguí-la no decorrer do tempo.

A termodinãmica dos processos irreversíveis resolve em parte este problema. Mas, além de ser muito complexa para ser tratada aqui, é como disse: resolve em parte. Não parece ser a solução definitiva. Esta me parece situar-se no ápice de um ramo mais simples da árvore da ciência. Um ramo que começa por nos exigir a análise de três conceitos importantes: a organização, a individualidade e a uniformidade.

Admitamos a existência de um grande número de tijolos, todos exatamente iguais e dispostos em inúmeras pilhas, lado a lado e num estado tal que possamos considerá-lo como de máxima organização; ou seja, numa disposição totalmente inútil mas, até certo ponto, estética. Trata-se também de um estado de uniformidade máxima: os tijolos são todos iguais e as pilhas idem. Há também um certo grau de individualidade, ou seja, cada tijolo é um indivíduo independente dos demais; o grau de liberdade depende, no entanto, da distribuição primitiva. Neste exemplo os tijolos, ainda que "ideologicamente" independentes, "seguram-se" uns aos outros, interagem-se. Logo, a individualidade não pode ser máxima; como também não é o grau de liberdade. Uma mesma região do espaço não pode ser ocupada por mais do que um tijolo.

Se espalharmos os tijolos pelo chão a organização diminuirá, desde que o espaço agora ocupado pelo conjunto, incluindo o intervalo entre dois tijolos, seja maior. A uniformidade diminuirá apenas quanto a um aspecto: não haverá mais pilhas iguais mas as unidades indivisíveis apresentam ainda uma uniformidade total. A individualidade, sob o aspecto "ideológico", é a mesma; mas o grau de liberdade é agora maior; as interações são mais fracas e, portanto, num "lacto sensu", a individualidade aumenta.

Se construirmos uma casa com os tijolos notaremos que a organização, à semelhança do exemplo anterior, será menor. Porém não tanto, pois os tijolos estão empilhados de uma forma ordenada, constituindo as paredes da casa. A individualidade se reduz bastante: não existem mais tijolos e sim paredes; e estas, conquanto sejam indivíduos, estão totalmente restritas a uma posição definida do espaço. A uniformidade também é reduzida pois o que era um conjunto de tijolos iguais transformou-se num conjunto de paredes diferentes.

Até que ponto a termodinâmica explica esta evolução? Nem explica e nem é pretensão da termodinãmica explicar este fenômeno; e nem poderia, mesmo que quisesse. A construção de uma casa é orientada por um arquiteto, um criador. E não há nenhuma lei da termodinâmica que o considere. Parece-me estranho que a mesma termodinâmica que não possui condições para explicar a evolução de uma pilha de tijolos manuseada pelo homem, pretenda explicar a evolução do Universo. Não digo que se deva admitir a existência de um Criador. O que eu quero deixar claro é que existe um ponto de interrogação que a mim não representa ainda um indeterminismo; e que a nossa ciência, muito comodamente, atribui ao acaso; ou ao Acaso, como querem alguns. O que eu quero deixar claro é que devem existir princípios outros que orientem a evolução do Universo. Da mesma forma que existem princípios que orientam o arquiteto na construção de uma casa para que ela se torne habitável; ainda que nem todos os arquitetos se preocupem com esse detalhe "secundário".

A porção do Universo que enxergamos está em evolução; e evoluindo para a complexidade, para a perda da uniformidade. Os átomos de Demócrito agruparam-se em partículas maiores; estas em átomos de Dalton; estes em moléculas; estas em macromoléculas; e estas em seres vivos. E estas modificações são tão irreversíveis quanto as demais que constatamos obedecer à segunda lei da termodinâmica; pelo menos na porção do Universo em que vivemos. Aliás, o simples fato de dizermos que o Universo evolui já nos dá o conteúdo essencial da segunda lei da termodinâmica a propor que "as transformações naturais são irreversíveis". A meu ver este conteúdo pode ser expandido para um princípio mais geral ao qual tenho chamado Princípio da Evolução do Universo: "O Universo evolui de um estado de organização e uniformidade máximas para um estado de organização e uniformidade mínimas, com redução concomitante da individualidade.

Pelo menos é o que se nota no Universo que se nos mostra. Não é impossível, no entanto, que além das fronteiras de um buraco negro ocorra justamente o contrário; e que estes sejam nada mais, nada menos, que organismos despoluentes do Universo, onde tudo volte a ser simplesmente os indivisíveis átomos de Demócrito; e estes, dotados exclusivamente de energia cinética, ou seja, de movimento, facilmente daí seriam liberados. Os buracos negros seriam então lixeiras cósmicas fantásticas, destinadas a inverter a evolução do Universo e reencaminhar os tijolos para um local onde pudessem novamente evoluir. E desta forma o Universo seria eterno.

Gostaria de deixar claro que o Princípio da Evolução do Universo constitui-se, a meu ver, numa norma geral de evolução, a qual deve estar baseada em princípios outros que não o "princípio do acaso" e muito menos o princípio da incerteza.

O texto termina aqui. Lembro de que quando o escrevi meus conhecimentos em física eram pouco mais do que rudimentares: Limitavam-se a física do segundo grau, a bio-físico-química do curso de graduação em medicina e à pós-graduação em fisiologia com área de concentração em biofísica do néfron (incluindo como créditos Termodinâmica dos Sistemas Biológicos, Mecânica dos Fluidos, Transporte através de Membranas Biológicas e outros). Não obstante, se fosse reescrever o tópico hoje mudaria muito pouca coisa.

Como disse acima, tentei apenas apresentar uma introdução aos tópicos fundamentais e relacionados às suas dúvidas. Estou aqui para possíveis esclarecimentos e/ou para ampliar o debate.

Olá Alberto,

Eu li seu mail e, como você já sabia, algumas coisas não ficaram muito claras para mim (Um simples aluno de Engenharia). O que me deixa mais confuso nesta tal de entropia é a sua equivalência aos fenômenos que ocorrem no nosso dia-a-dia. E é impressionante como a física se preocupa em explicar quase tudo para as pessoas. Quem diria que até pra mostrar porque é ruim arrumar o quarto a física mostra o porquê.

Olha, estou tentando assimilar algumas coisas mas vou continuar precisando da sua ajuda. Por exemplo:

No meu livro de física eles falam sobre processos reversíveis e irreversíveis... Mas não explicam muito claramente as diferenças entre esses dois processos. E como nós podemos saber (eu acho que sei), quando estamos diante de um processo reversível a variação de entropia do sistema mais a variação de entropia do ambiente é nula qualquer que seja o processo reversível. Mas, o mais intrigante nisto, é saber como nós podemos organizar uma coisa desorganizando outra... Quem pode me garantir que quando o pistão sobe e as moléculas do gás no recipiente ficam com maior grau de liberdade ou seja mais "desorganizadas" o ambiente fica mais organizado". Nem sei ao menos se estou usando os conceitos corretos, mas, sei que estou diante de assunto muito complicado.

Espero não estar sendo mais complicado do que o próprio conceito de entropia...

O que determina um fenômeno ser ou não espontâneo??? Porque na química nós estudamos entalpia e na física não??? Será que qualquer tipo de fenômeno ou ação é reversível ou irreversível????

Mais confuso do que nunca e ávido por respostas,

Andre Camello

André escreveu:

André: No meu livro de física eles falam sobre processos reversíveis e irreversíveis... Mas, não explicam muito claramente as diferenças entre esses dois processos.

Reversibilidade é um termo que deve ser interpretado com muito cuidado, principalmente para aqueles que pretendem entender a termodinâmica. A termodinâmica não estuda apenas a evolução de sistemas isolados mas também, e principalmente, a interação entre sistemas. Ao pensarmos em reversão de um "processo" não podemos fixar nossa atenção em apenas um dos sistemas participantes mas em todos. O processo terá sido revertido, do ponto de vista termodinâmico, se, e somente se, "todos" os sistemas participantes tiverem retornado ao estado primitivo. Por outro lado, não é necessário, para dizermos que um processo é reversível, que a reversão tenha ocorrido. É suficiente mostrar a possibilidade teórica desta reversão.

Antes de prosseguir convém chamar a atenção para a importância dos processos em que "pelo menos um" dos sistemas retorna ao seu estado original (e, portanto, nem sempre são processos reversíveis). O estudo destes processos é importantíssimo para o entendimento da primeira lei da termodinâmica, que apóia-se no conceito de transformações equivalentes: "duas transformações são equivalentes (não só, mas também) quando, após passar por ambas transformações, o estado inicial e final de um dos sistemas que interage for o mesmo". O princípio que está por trás da primeira lei da termodinâmica é o Princípio da Equivalência a dizer que "duas transformações equivalentes a uma terceira são equivalentes entre si" [recentemente escrevi algo a respeito — está na msg 2468 da Ciencialist — a demonstrar o parentesco entre este princípio e a primeira lei].

Outro caráter importante com respeito aos processos reversíveis é sua idealidade. Quase sempre, quando falamos em processos ou transformações reversíveis, estamos nos referindo a processos que na prática não existem como tais. Ora, dirá você: Se não existem como tais, porque estudá-los? Seria apenas "encucação" ou "maluquice" presente na cabeça dos físicos teóricos? Pois eu digo que é fundamental entender o porquê desta "maluquice", razão pela qual destinarei boa parte desta msg a explicá-la e, oportunamente (em outras msgs), retornarei aos seus outros questionamentos.

A idealidade está para a física assim como o conceito de limite está para a matemática. Aliás, creio mesmo que o conceito de limite entrou na matemática pela porta dos fundos, como decorrência da constatação de que os físicos conseguiam prever transformações reais a partir de considerações ideais. Uma transformação ideal pode ser encarada como o limite de uma transformação real quando uma das variáveis tende a zero. Galileu, por exemplo, estudou condições em que, pela redução do atrito, poderia conceber a lei da inércia [aliás, a inércia de Galileu, ao que tudo indica, era circular — provavelmente aqui na Terra deveria seguir uma geodésica, sendo portanto praticamente retilínea para as pequenas distâncias do dia-a-dia]; o mesmo Galileu deve ter imaginado que pela redução da resistência do ar chegaríamos à lei da queda livre, afirmando desta maneira que corpos de mesma massa, e no vácuo, cairiam de maneira idêntica num campo gravitacional [É interessante salientar que a experiência que demonstrou a existência do vácuo, foi sugerida por Galileu a seu discípulo e sucessor acadêmico Torricelli]. Não estranhe portanto a valorização, pelos físicos, dos processos reversíveis, ainda que eles não existam como tais no mundo macroscópico.

O que há de estranho na termodinâmica não é a idealidade em si mas a maneira como ela é abordada. Como vimos acima, na mecânica chega-se a leis limites (por exemplo, inércia e queda livre) partindo-se da experimentação na qual "visualizamos" uma das variáveis tender a zero [por exemplo, através da lubrificação podemos reduzir gradativamente o atrito e extrapolar os resultados para um atrito nulo]. A termodinâmica, no entanto, não chega a uma lei limite [no caso a segunda lei] a partir da experimentação mas parte da segunda lei a dizer que "os fenômenos naturais observados no mundo macroscópico são irreversíveis" [esta seria uma maneira atípica de enunciarmos a segunda lei da termodinâmica]. Ou seja, a lei assume a reversibilidade como algo impossível de ser alcançado a não ser numa condição limite. Dito de outra maneira, não chegamos à lei pela observação de condições limites mas sim por afirmar a existência de uma condição, qual seja a reversibilidade, que jamais poderia ser alcançada, nada obstando a que se pudesse se aproximar cada vez mais dessa condição [e é sob esse aspecto que se encaixa o limite]. Poderia então dizer que a segunda lei da termodinâmica não é consequência da experimentação mas sim que sustenta-se pela experimentação (até hoje não se conseguiu negá-la, por mais que tenha sido tentado, principalmente no século dezenove).

Outro aspecto interessante da termodinâmica é a sua generalidade, pois ela tem se mostrado válida para interações entre sistemas mesmo quando não entram em jogo trocas de calor. Poderíamos mesmo chamá-la de "Dinâmica das Transformações e/ou Interações entre os Sistemas" caso quiséssemos enfatizar sua generalidade. É importante verificar que a entropia de um sistema pode aumentar mesmo que ele passe por um processo onde não estejam envolvidas trocas de calor como, por exemplo, a expansão de um gás confinado em um recinto com paredes adiabáticas. Como então calcular a variação da entropia nestes casos? Este é um problema que, com grande frequência, atormenta os estudantes.

Outra característica da termodinâmica, e relacionada a sua generalidade, reside no fato de seus princípios fundamentais poderem ser enunciados de inúmeras maneiras. E o interessante é verificar que se algum dia conseguirmos negar um único destes enunciados, poderemos, por raciocínios lógicos, concluir pela negação de todos os demais.

Perceba que até agora eu apenas conceituei a reversibilidade e/ou a irreversibilidade, sem entrar nas questões operacionais e que são importantes para que possamos entender como os físicos chegaram a sentir a necessidade de propor a conceituação da entropia, ao perceberem que estavam diante de algo capaz de se sujeitar à mensuração. Antes porém vale a pena considerar alguma coisa sobre um dos questionamentos que você apresentou na primeira mensagem, qual seja, "Entropia = Desordem?" e que relaciona-se com a maioria das outras dúvidas que você tem apresentado.

Como já afirmei em msg anterior, podemos pensar na entropia como retratando a "medida" da desordem de um sistema. Não obstante, é importante frisar que esta interpretação para a entropia, rigorosamente falando, está além do escopo da termodinâmica. A termodinâmica é reconhecida como "o paradigma da teoria fenomenológica" (Mario Bunge, 1974, Teoria e Realidade, Ed. Perspectiva, São Paulo) e, para ser coerente consigo mesma, não deve penetrar em terrenos representacionais. A idéia de entropia como desordem deriva da mecânica estatística clássica, uma teoria representacional que, a exemplo da teoria quântica, não conseguiu substituir e/ou explicar a termodinâmica em toda a sua extensão, conquanto seja útil em inúmeras condições. Podemos então meramente conjeturar sobre o significado da entropia, da maneira como ela se mostra para um estudioso de termodinâmica, e verificar até que ponto este conceito adapta-se às idéias acrescentadas pelos estudiosos da mecânica estatística. Não há nada a nos garantir, a não ser a lógica bem fundamentada da mecânica estatística, que a entropia desta teoria seja exatamente a mesma estudada em termodinâmica.

Ainda sob o ponto de vista da teoria do conhecimento, ou epistemologia, podemos questionar, por outro prisma, a respeito da identidade entre a "entropia de um sistema" e a "medida da desordem deste sistema". A esse respeito é interessante o seguinte comentário exposto na Enciclopédia Britânica (no capítulo "Principles of Physical Science"): "A entropia assume um valor numérico que pode ser atribuído a um sistema pela experimentação e, a menos que possamos definir a desordem com a mesma precisão, qualquer relação entre as duas estará dotada de pouco significado não servindo portanto de fundamento para qualquer dedução. Embora exista muito de verdade na visão ingênua de relacionar aumento de entropia a desordem, não há como se progredir, ao se utilizar este procedimento, sem uma definição muito mais precisa do que seja desordem."

Na próxima mensagem tentarei comentar alguma coisa mais a respeito de reversibilidade/irreversibilidade. Provavelmente precisarei anexar algumas figuras que ainda estou construindo, e portanto pode ser que demore um ou dois dias. Não sei se a lista aceita mensagens com figuras em anexo mas, se não aceitar, colocarei as figuras em meu Web Site pessoal de forma que, estando conectado à Internet, qualquer pessoa possa acessá-las com um clique. Se houver alguma dúvida quanto ao comentado acima, não deixe de relatar. Se houver alguma outra dúvida a ser acrescentada àquelas que reproduzo abaixo, e ainda não respondidas, esteja à vontade para tal.

Questões pendentes:

E como nós podemos saber (eu acho que sei), quando estamos diante de um processo reversível, a variaçao de entropia do sistema mais a variaçao de entropia do ambiente é nula para qualquer processo reversível. Mas, o mais intrigante nisto, é saber como nós podemos organizar uma coisa desorganizando outra... Quem pode me garantir que quando o pistão sobe e as moléculas do gás no recipiente ficam com maior grau de liberdade ou seja mais "desorganizadas" o ambiente fica mais "organizado". Nem sei ao menos se estou usando os conceitos corretos, mas, sei que estou diante de assunto muito complicado.

O que determina um fenômeno ser ou não espontâneo??? Porque na química nós estudamos entalpia e na física não??? Será que qualquer tipo de fenômeno ou ação é reversível ou irreversível????

Olá, André

Na msg anterior eu apenas conceituei a reversibilidade e/ou a irreversibilidade, sem entrar nas questões operacionais. Vamos tentar evoluir nesse sentido.

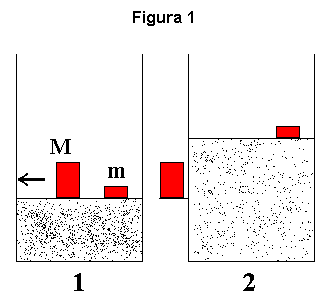
A figura 1 retrata classicamente a expansão de um gás contido num recipiente dotado de um êmbolo ou pistão (membrana móvel supostamente de massa desprezível) e inicialmente em repouso graças a um equilíbrio de forças devidas a:

1. pressão do gás;
2. pressão atmosférica;
3. massa M; e
4. massa m.

Dentre as aproximações que poderíamos considerar como relacionadas à "idealidade do processo imaginado" realça a ausência de atrito do pistão com as paredes do recipiente. A ausência de massa da membrana móvel é compensada pela massa m e, portanto, sob esse aspecto, não estamos assumindo idealidades (essa massa não será modificada nem retirada do sistema durante suas possíveis transformações). É costume também considerar o meio exterior como sendo o vácuo e, portanto, sua pressão é igual a zero. Desta forma a massa m torna-se fundamental, pois acaba sendo a única resistência a uma expansão sem limites quando subtrairmos a massa M de cima do êmbolo.

Existe ainda uma "idealidade própria à termodinâmica", qual seja, a termodinâmica estuda estados iniciais e estados finais, sem se preocupar com o processo em si a levar do estado inicial ao final. Por exemplo, não teria sentido, sob o ponto de vista da termodinâmica, pensar em velocidades ou acelerações das massas envolvidas; também não teria sentido supor que o êmbolo viesse a oscilar antes de atingir um estado final. Aliás, se pensássemos nesta oscilação, o estado final jamais seria atingido pois, como descrito acima, desprezamos o atrito do pistão com as paredes do recipiente. Estas idealidades dão uma certa aparência de fragilidade à termodinâmica, fragilidade esta que desagrada a muitos, em especial àqueles que iniciam o estudo da termodinâmica logo após terem dados os primeiros passos em mecânica. Não obstante, é tão bonita a filosofia que se segue a partir destas considerações "absurdas" iniciais e são tão profícuas as aplicações que decorrem dos conceitos que advém logo após termos "engolido" essas considerações iniciais, que ficamos tentados a aceitá-las sem discussões (mesmo porque, e como já disse, as teorias que tentaram substituir a termodinâmica, até hoje não nos levaram a nada melhor). Perceba então o porque da termodinâmica ser considerada "o paradigma das teorias fenomenológicas, não se preocupando em descrever fenômenos de calor, mas propriedades muito gerais e leis, com a ajuda de construtos de alto nível tais como energia E e entropia S" (Mario Bunge, op.cit).

É comum dizer-se que a termodinâmica justifica o "instrumentalismo que se apóia nos critérios de utilidade" e a afirmar que "a boa teoria é aquela que funciona". Temos aí um resquício ou evolução da doutrina empirista que chegou a ter bastante adeptos no século passado. Não obstante, não tenha dúvida de que é muito mais fácil justificar o empirismo pelos sucessos da termodinâmica do que o inverso. De qualquer forma o que acho importante frisar é que se tentarmos "mecanizar" a termodinâmica, deixando seus alicerces filosóficos de lado, não mais estaremos estudando termodinâmica, embora possamos estar evoluindo em direções várias, a maioria das quais já foram testadas e não deram frutos.

Voltemos à figura 1. Entre os estados inicial (1) e final (2) simplesmente retiramos a massa M de cima do êmbolo e, por questões de ordem didática, conservamos esta massa na altura primitiva. Poderíamos ter imaginado a massa M em cima de uma haste presa ao êmbolo e tal que não precisasse "atravessar a parede do recipiente" (na prática deve-se proceder a manobras semelhantes a esta e que não são representadas afim de não poluir a figura, ainda que tais atitudes, com grande frequência e por não serem devidamente comentadas, acabam por desorientar os estudantes).

A transformação 1Þ2 é um exemplo clássico de processo irreversível. Não há como o sistema evoluir, por si só, do estado final para o inicial (o que reverteria o processo, pois M continua em sua altura inicial), a menos que, por processos outros elevássemos a massa M, colocando-a novamente em cima do êmbolo. Poderia então aproveitar esse exemplo para começar a responder a outro de seus questionamentos, qual seja:

O que determina um fenômeno ser ou não espontâneo?

Pergunto então: após termos retirado a massa M de cima do pistão, o que fez com que o gás se expandisse até o estágio final? Não teria sido o desequilíbrio de forças? Você poderia questionar dizendo que ao retirar a massa M induzimos esta espontaneidade. É verdade, porém após a retirada da massa o gás ficou sujeito a se comportar de duas maneiras possíveis: ou permaneceria em seu estado 1, ou evoluiria para um outro estado qualquer. Por algum motivo ele nem permaneceu no estado 1 e nem evoluiu para outro estado que não o 2. E esta evolução, sem dúvida alguma, foi espontânea, obviamente, repito, como consequência de termos retirado a massa M de cima do pistão. Aliás, toda a evolução de um estado de equilíbrio para outro estado de equilíbrio dá-se após algum agente externo ter modificado alguma característica do sistema; logo a seguir, e supondo que o observador responsável pela modificação instantânea não mais interfira sobre o sistema, a evolução do mesmo será espontânea.

Se tentarmos explicar a espontaneidade de maneira mais profunda, estaremos evoluindo para o representacionismo e deixando a filosofia termodinâmica de lado. Não é impossível que, ao pensar em espontaneidade, alguém lembre-se da lei da inércia, a retratar uma espontaneidade permanente: um corpo, livre da ação de forças, conserva permanentemente seu estado de movimento. Perceba que um objeto nestas condições, embora em movimento "relativo", está em equilíbrio e o que caracteriza este equilíbrio é a manutenção de sua velocidade. Se durante um certo tempo exercermos uma força a este objeto, após cessar a força ele manterá seu novo estado de equilíbrio. No referencial adotado poderíamos dizer que o objeto passa agora a, espontaneamente, ocupar posições espaciais diferentes, para um mesmo tempo, do que viria a ocupar caso mantivesse seu estado primitivo (perceba o "nó" que eu precisei dar para adequar as palavras a essa situação que, sem dúvida alguma, parece-me ser a mais elementar em termos de espontaneidade).

Sob certos aspectos, e sem contrariar a filosofia da termodinâmica, podemos dizer que a lei da inércia é um caso muito especial do Princípio da Continuidade que costumo enunciar como: "Se as propriedades de estado de um sistema isolado permanecerem inalteradas em observações sucessivas não periódicas, elas permanecerão inalteradas enquanto persistir o isolamento". [Este princípio, ao lado de outros, pode ser encontrado no artigo Eletromagnetismo e Relatividade]. Para chegar à lei da inércia pense na velocidade como a propriedade de estado e o isolamento como a ausência de forças.

Voltarei ao tema reversibilidade/irreversibilidade na próxima mensagem.

Olá para todos...

Sou estudante de 2º grau e também estou meio confusa a respeito de entropia...

Estudo pelo livro "Fundamentos de Física", do Halliday...

Este livro não define entropia... mas tbm cita processos reversíveis e não reversíveis... E associa entropia como variável da segunda lei, como temperatura é variável da lei zero e energia interna é variável da primeira...

Sr. Alberto, li seu texto, mas ainda estou meio confusa... Entropia é a "seta"do tempo?

[ ] s
Tathiana

Tathiana escreveu:

Tathiana: Olá para todos...
     Sou estudante de 2º grau e também estou meio confusa a respeito de entropia...

Esta confusão é normal. A entropia não é nada do outro mundo mas também não é um conceito trivial. Mesmo depois de acreditarmos que aprendemos alguma coisa a respeito do tema, flagramos situações a nos desorientarem totalmente. Estudo esporadicamente este assunto há mais de duas décadas e estou convencido de que ainda não o assimilei em toda a sua plenitude.

Existe um pensamento devido a Bohr, um dos precursores da física moderna, e que diz o seguinte: "Quem nunca duvidou da mecânica quântica, certamente não entendeu a física quântica". Com respeito à entropia eu mudaria um pouco este pensamento e diria: Quem nunca estranhou a entropia, ou seja, nunca ficou confuso a respeito do tema, certamente não entendeu a entropia. Se o pensamento for verdadeiro, o corolário que surge é o seguinte: Você está a meio do caminho e, se prosseguir, chegará lá.

Quanto ao fato de estar no 2º grau, não creio ser este um fator limitante. Pode-se compreender a entropia mesmo com os conhecimentos matemáticos do estudante de 2º grau. A matemática da termodinâmica não é muito elementar, pois envolve equações com derivadas parciais; porém isso vem após o perfeito entendimento dos conceitos e chega-se às equações fundamentais, que não são tão complicadas, por um caminho quase puramente filosófico. A dificuldade inicial da termodinâmica relaciona-se justamente a sua natureza filosófica e talvez resida aí o motivo principal da confusão que se apossa de nós, quando iniciamos seu estudo.

Tathiana: Estudo pelo livro "Fundamentos de Física", do Halliday... Este livro nao define entropia... mas tbm cita processos reversíveis e não reversíveis...

O entendimento da reversibilidade/irreversibilidade é fundamental para o entendimento da entropia. Não estou de posse do Halliday e portanto não posso comentar a respeito. É possível que ele tenha passado rapidamente pela definição, relacionando-a de alguma forma à reversibilidade, e a passagem não tenha ficado muito clara. É comum os livros didáticos evitarem o aprofundamento desta passagem, o que não deixa de ser paradoxal (afinal, se o livro é didático, deveria ser claro na introdução dos conceitos).

Tathiana: E associa entropia como variável da segunda lei, como temperatura é variável da lei zero e energia interna é variável da primeira...

Com efeito, cada uma destas leis justifica a conceituação de uma destas variáveis de estado, e a segunda lei justifica a introdução da entropia. Mas a segunda lei nada mais é do que a afirmação de que "os fenômenos naturais são irreversíveis" quando estudados em escala macroscópica. Por exemplo, "o calor passa espontaneamente de um corpo quente para um corpo frio, não ocorrendo o inverso" (se ocorresse o inverso seria possível revertermos o processo).

A reversibilidade, como estou tentando demonstrar nas outras mensagens, existe apenas em condições limites e hipotéticas. Existir em condições limites implica em que podemos, experimentalmente, aproximarmo-nos desta reversibilidade, ou seja, imaginar processos que estão cada vez mais próximos desta condição ideal (na próxima msg tentarei mostrar como isto é possível para o sistema gás-êmbolo-peso).

Apenas para registrar o fato, e para que vocês possam me cobrar oportunamente, caso esqueça de relatá-lo, lembrarei que à medida que nos aproximamos desta idealidade (situação de irreversibilidade), aproximamo-nos também da situação de equilíbrio, ou seja, chegamos a alterações de estado bem pequenas e tais que ao passarmos de um estado para o outro possamos dizer que o sistema sofreu um processo de "quasi-equilíbrio".

Existe no mundo microscópico transformações em nível molecular que passam despercebidas para nós. Por exemplo, num gás em equilíbrio acontecem inúmeras colisões moleculares que não se refletem por alteração macroscópica alguma (a pressão, o volume e a temperatura permanecem constantes). Estas pequenas alterações são, pelo menos em teoria, reversíveis. Digo em teoria pois ao imaginarmos um cálculo médio destes processos, chegando assim às variáveis intensivas macroscópicas (pressão, temperatura), por mais que as moléculas tenham variado sua posição, velocidade, etc., o estado final é igual ao inicial. Perceba então que o sistema se altera microscopicamente mas permanece em equilíbrio macroscópico. Existem também alterações microscópicas irreversíveis e são exatamente estas que denunciam, através das médias calculadas antes e depois, a passagem de um estado macroscópico para outro, agora irreversível. Lembro ainda que estas considerações fogem do escopo da termodinâmica e um estudo aprofundado é objeto de teorias outras, tais como a mecânica estatística. Relatei aqui apenas na tentativa de justificar, por um raciocínio não termodinâmico, um dos sentidos da expressão "quasi-equilíbrio".

Tathiana: Entropia é a "seta"do tempo?

Esta afirmação pode ser verdadeira, entropia = seta do tempo, mas não é objeto do estudo da termodinâmica. A termodinâmica estuda sistemas em transformação, logo existe um "antes" e um "depois", ainda que o processo em si, tanto o que acontece entre um estado e outro, quanto a duração do processo, seja literalmente deixado de lado. Ao estudarmos um estado "inicial" A e outro estado "final" B, percebemos que é impossível o sistema, após passar de A para B, retornar espontaneamente para A (isto é garantido pela segunda lei, cuja lógica estou ainda tentando expor). Podemos efetuar essa transformação de B para A, porém modificaremos algum outro sistema (frequentemente chamado como o restante do Universo). E seria impossível que o sistema retornasse para A sem deixar nenhuma marca no restante do Universo a testemunhar que o processo primeiro (transformação de A para B) realmente ocorreu. Resumindo: sempre que observamos uma transformação sabemos, de antemão, que será impossível o Universo retornar ao que era antes da transformação. Isto retrata como, em decorrência do segundo princípio da termodinâmica, poderíamos inferir pela impossibilidade do retorno ao passado. Como medimos esta irreversibilidade através da entropia, alguns gostam de dizer que a entropia é a "seta" do tempo. O termo "seta" se justifica, pois a termodinâmica garante a direção do processo entre o "antes" e o "depois" mas não a duração ou o intervalo de tempo entre o "antes" e o "depois".

Tathiana: Sr. Alberto, li seu texto, mas ainda estou meio confusa...

Espero ter colaborado para promover alguma compreensão, ainda que com a certeza de ter aumentado bastante a confusão. A esse respeito cheguei a escrever, há alguns anos, algo parecido com: "Com grande frequência, e para aprender, somos obrigados temporariamente a engolir determinados conceitos, e isto nos dá azia. Pois aprender é saber conviver permanentemente com esta azia. E o gostoso é quando ela passa. Dá até vontade de tê-la de novo, só para sentir aquela sensação ao passar. Às vezes se cronifica, e isso é um perigo; deixa de nos incomodar e absorvemos um dogma."

Continuação da Mensagem 05

Olá André e demais companheiros da lista fisica@news.com.br

Dando prosseguimento ao tema apresentado nas mensagens anteriores, vamos realizar a mesma expansão descrita para o gás da figura 1, porém agora por etapas. Ou seja, vamos dividir a massa M em três massas menores e iguais a M/3 mostradas na figura 2 (cada pequena massa não necessita ser igual a m, aquela que, ao final, permanece em cima do êmbolo). O estado final poderá ser idêntico ao da experiência anterior, porém o processo é bastante diferente.

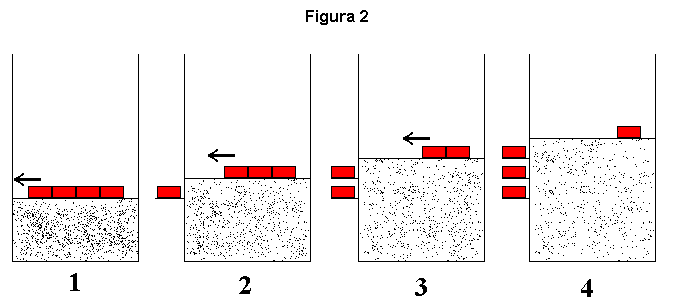
Porque eu disse "poderá" e não "será" idêntico? Bem, digamos que pelo menos uma das paredes do recipiente permita trocas de calor e que o sistema esteja, por esta parede, em contato permanente com uma fonte de calor a uma temperatura constante T. Desta forma, independentemente do sistema sofrer a alteração proposta na figura 1 ou aquela proposta na figura 2, a temperatura final do gás será T. Sua pressão p, ao término da transformação, será igual nos dois casos, pois é a pressão que equilibra a massa m. Logo, e como o sistema é fechado (não há troca de matéria), todas as demais variáveis serão iguais, incluindo o volume. Ou seja, para transformações isotérmicas o estado final do gás será o mesmo nos dois casos.

Que dizer da irreversibilidade?

Seguindo uma linha de raciocínio idêntica à apresentada na mensagem anterior, podemos concluir que este processo também é irreversível. Porém, se formos classificar, ou dar um peso à irreversibilidade, notaremos uma diferença sutil quanto a esse aspecto. Obviamente, somente poderemos evoluir nesta direção após definirmos muito bem os critérios a serem utilizados para medir ou dar pesos ao que se nos mostra como caráter irreversível de cada um dos processos.

Perceba então agora que, para o sistema gás, mostrado na figura 1, retornar ao estado primitivo, uma maneira simples seria elevarmos a massa M de uma altura h igual à diferença de alturas do êmbolo entre o estado inicial (1) e o estado final (2). Logo a seguir depositamos a massa M em cima do êmbolo e esperamos pela "reversão" da transformação sofrida pelo gás, com o que a massa M também retornará a sua posição original. Porém, o universo não retornará à situação primitiva. De alguma forma, e para elevar a massa M, modificamos "alguma coisa" deste universo e não representada no esquema. Esta "alguma coisa" realizou um trabalho W' ao elevar a massa M de uma altura h. Ou seja, W' = Mgh e este é o saldo negativo do "restante do universo": ou seja, o universo perdeu "capacidade de realizar um trabalho" W' = Mgh.

É importante não confundir esse trabalho W', a caracterizar uma propriedade perdida pelo universo (capacidade de realizar trabalho) com o trabalho de expansão realizado pelo gás ao elevar a massa m e que, neste caso, será W = mgh.

Se pensarmos na primeira lei da termodinâmica diremos que, de alguma forma, ao passar pelo processo de ida e de volta, a fonte de calor ficou com um "saldo positivo de calor", ou seja, recebeu mais calor na contração do que cedeu na expansão, e a diferença iguala o trabalho W'. Como a fonte pertence ao que denominamos "restante do universo", o conteúdo energético do universo permanece inalterado (aceitando-se a equivalência entre calor e trabalho como uma identidade em termos de energia — primeira lei).

Seria o trabalho W' uma boa medida a retratar a irreversibilidade? Antes de responder à pergunta pense nas restrições impostas (limitamo-nos, por enquanto, a estudar transformações isotérmicas). Por outro lado, e admitindo-se que para transformações isotérmicas a resposta fosse positiva, uma segunda pergunta seria: E se pensarmos não no trabalho W' em si, mas no que o universo perdeu, qual seja, a "capacidade de realizar trabalho" e que, de alguma forma, foi compensada por um "saldo positivo de calor"? Estaríamos evoluindo no sentido de uma generalização?

Tente agora adaptar o raciocínio acima demonstrado para uma possível "reversão" da transformação sofrida pelo gás no processo apresentado na figura 2. Compare com o discutido para as transformações de "ida" e "volta" do processo apresentado na figura 1. Na sua opinião: A irreversibilidade dos dois processos parece ser idêntica ou equivalente? Nota-se alguma diferença importante? Se sim, o trabalho W' seria uma boa medida para estimar algum conceito definido a partir desta diferença? Se não conseguir responder a estas perguntas, não se desespere. Se achar que a dúvida é importante, não deixe de escrever (e isto vale para os demais que estão acompanhando estas mensagens sequenciais). Caso contrário, aguarde a próxima mensagem, pois começarei por aí.

Olá Todos, Mais especificamente Olá Alberto.

Nao quero atrapalhar o ritmo do debate a respeito da termodinâmica e suas leis, até por que, esse assunto me interessa bastante e eu estou tentando prestar bastante atenção nas suas explicações... Mas Gostaria de saber uma coisa...

Você falou no mail a Tatiana (olá, Tatiana), que

Alberto: Esta afirmação pode ser verdadeira, entropia = seta do tempo, mas não é objeto do estudo da termodinâmica.

Isso é o mesmo que dizer que as coisas tendem a se desorganizarem?? A expansão do Universo??

OBS: Desculpa se estou tirando conclusoes precipitadas, antes do tempo, mas é que eu achei que havia achado uma correlaçao entre essas duas perguntas... estou errado nao é??

André escreveu:

André: Nao quero atrapalhar o ritmo do debate a respeito da termodinamica e suas leis, até por que, esse assunto me interessa bastante e eu estou tentando prestar bastante atençao nas suas explicaçoes... Mas Gostaria de saber uma coisa...

Fique a vontade. Tenho procurado seguir uma certa sequência, mas não é nada que não possa ser modificado quando surgirem dúvidas. Para dizer a verdade, estou improvisando em cima de seus questionamentos iniciais, sem me preocupar em seguir outra sequência que não a necessária para explicá-los. Felizmente a termodinâmica comporta vários caminhos. Só para exemplificar: a segunda lei é resultante dos trabalhos de Carnot, efetuados por volta de 1820; a primeira resulta dos trabalhos de Mayer (algo em torno de 1835-40) e posteriormente de Joule (1843, se não me engano); mais tarde "descobriu-se" a lei zero (o princípio do equilíbrio térmico), sem o qual não teria sentido se falar em temperatura (ainda que já se conhecesse a temperatura). Ou seja, a termodinâmica foi construída de trás para a frente, o que mostra a independência quase que total entre os seus princípios. Além disso seus princípios podem ser enunciados de várias maneiras, o que comporta inúmeros enfoques diferentes e não aprisionados a uma metodologia pedagógica única.

André: Você falou no mail a Tatiana (olá, Tatiana), que

Alberto: Esta afirmação pode ser verdadeira, entropia = seta do tempo, mas não é objeto do estudo da termodinâmica

André: Isso é o mesmo que dizer que as coisas tendem a se desorganizarem?? A expansão do Universo??

Não diria que é a mesma coisa, mas sim que existe uma relação entre as idéias. Pela segunda lei chegamos a concluir que a termodinâmica é coerente com uma direção única para o tempo. E como a entropia foi a grandeza escolhida para caracterizar esta lei, podemos dizer que a identidade "entropia = seta do tempo" faz sentido para os estudiosos do tema. Por outro lado, também pela segunda lei conclui-se que a termodinâmica é coerente com um espalhamento (expansão dos gases no vácuo, o exemplo clássico de irreversibilidade) ou então com a propensão para a mistura. Via de regra, e a menos que existam outros fatores de ordem estrutural a impedir ou dificultar a mistura, é muito mais fácil misturar do que separar as partes, da mesma forma que é muito mais fácil sujar um objeto (mistura com impurezas) do que limpar. Não há nenhuma lei que proíba a purificação ou limpeza espontânea de um objeto; no entanto, o que usualmente verificamos é o contrário: os objetos se sujam mesmo quando fora de uso. Quanto às proibições da segunda lei, eu diria que a rigor a segunda lei não proíbe nada: ela simplesmente chama a atenção para uma impossibilidade natural. Nós é que, por acreditarmos na veracidade da afirmação, e pelo não encontro, no decorrer dos séculos, de exceções à regra, somos compelidos a aceitá-la como uma proibição natural.

A desordem referida como inerente à segunda lei tem muito a ver com o espalhamento ou expansão descritos. Perceba que a mistura também retrata uma expansão de um sistema no seio do outro. Por outro lado, no sentido rotineiro do termo, ordenar muitas vezes relaciona-se a separar objetos semelhantes; e sob esse aspecto, misturar objetos diferentes relacionar-se-ia a desordenar o sistema composto. Existe também a ordem no sentido da concentração: por exemplo, se agruparmos todos os nossos livros na biblioteca, teremos um certo grau de ordem; se eles estiverem nas estantes, a ordem será maior; mas se os espalharmos pela casa poderemos dizer que eles estão desordenados. Provavelmente foram analogias deste tipo que levaram os termodinâmicos do século passado a concluírem que, por sua segunda lei, a termodinâmica propõe uma evolução do universo no sentido da desordem (espalhamento de seus constituintes microscópicos). A expansão do universo em nível cosmológico (afastamento das galáxias) parece-me não ter sido ainda contemplada, pelo menos sob um aspecto rigoroso e axiomático, pela termodinâmica, mas não é impossível que um dia isso venha a ser feito.

Em resumo: a entropia de um sistema isolado ou permanece constante (sistema em equilíbrio) ou aumenta; o Universo é um sistema isolado e não está em equilíbrio, logo sua entropia está em ascensão; como a entropia do Universo sempre aumenta, isto permite-nos dar um sentido termodinâmico ao tempo (entre duas situações do Universo, o "antes" representa o estado de menor entropia); por outro lado, entropia relaciona-se a grau de espalhamento, expansão, miscigenação, desordem enfim. Conclusão: o Universo, sob esse aspecto, evolui para a desordem. No meu modo de ver, essas conclusões são um pouco precipitadas, haja vista que apóiam-se na veracidade de uma teoria corroborada para sistemas laboratoriais e não cosmológicos. A história, por outro lado, tem nos mostrado uma outra característica da evolução do Universo: O conhecimento humano aumenta e as teorias caem, sendo substituídas por outras.

André: OBS: Deculpa se estou tirando conclusoes precipitadas, antes do tempo, mas é que eu achei que havia achado uma correlaçao entre essas duas perguntas...

Como disse acima, fique a vontade e exponha suas dúvidas assim que aparecerem. Se não puder ajudá-lo pelo menos ficarei ciente de que não estou sozinho no pedaço.

André: ...estou errado nao é??

Pelo visto, não!! A correlação existe.

Continuação da Mensagem 08

A "reversão" da transformação sofrida pelo gás apresentado na figura 2 (transformação isotérmica e em três etapas) está mostrada na figura 3 (abaixo) e esta deve ser "lida" da direita para a esquerda. Parece ficar claro aí que o único trabalho que o "restante do universo" deve realizar, para atingir o objetivo proposto, relaciona-se à elevação de uma das massas iguais a M/3, exatamente aquela que, no suporte, situa-se mais abaixo, e deve ser elevada da mesma altura h utilizada nos cálculos efetuados no caso anterior (transformação em uma etapa da figura 1). As demais massas M/3 são simplesmente deslocadas lateralmente, não havendo necessidade da realização de trabalho no sentido termodinâmico do termo.

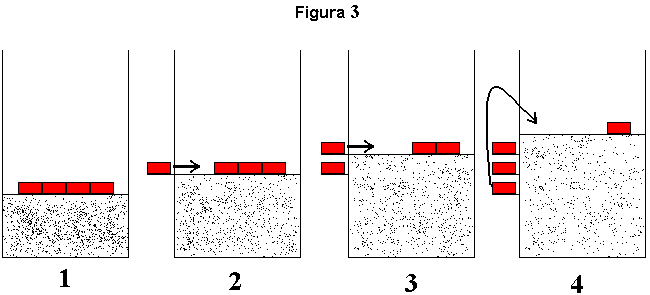
Neste segundo caso, após o gás retornar ao seu estado primitivo o "restante do universo" perdeu uma capacidade de realizar trabalho igual a W'' = (M/3)gh, ou seja, 1/3 de W'. Ficamos então tentados a imaginar que se o número de etapas fosse igual a 20 o "prejuízo" sob esse aspecto seria reduzido para W''' = (M/20)gh = 1/20 de W'. E se aumentássemos o número de etapas de tal maneira que a massa M fosse, na realidade, um monte de areia e, no processo de "ida", fossemos retirando os grãos um a um até que apenas persistisse a massa m sobre o êmbolo? O número de etapas seria muito grande, a duração seria muito aumentada e o processo seria estafante. Chegaríamos, no entanto, a uma situação em que W'* seria extremamente pequeno. Ou seja, seria suficiente elevarmos um grão de areia da altura h para iniciarmos a "reversão" da transformação. A perda do "restante" do universo seria diminuta e o processo seria quase reversível, a despeito das dificuldades de ordem operacional (número de etapas, duração, etc.). Um passo além e chegamos aos "infinitésimos" de massa. Ou seja, no limite, quando o número de etapas tende a infinito, e portanto, a massa de cada fração em que M foi subdividido tende a zero, o trabalho que teríamos de realizar afim de "reverter" a transformação seria igual a W'* = (M/infinito)gh = 0. Rigorosamente falando, diria que chegamos à reversibilidade a menos de um infinitésimo, e a capacidade de realizar trabalho do "restante do universo" permaneceu inalterada, a menos de um infinitésimo.

Respondendo então às perguntas pendentes, diria:

1. O trabalho W' é uma boa medida a retratar a irreversibilidade de transformações isotérmicas como aquelas apresentadas.
    
2. Duas transformações isotérmicas com estados inicial e final idênticos podem não ser idênticas com respeito à reversibilidade, ainda que possamos dizer que são "equivalentes" no sentido expresso na mensagem 4. Na conceituação de equivalência o "restante do universo" não é levado em consideração; o conceito de equivalência relaciona-se intimamente com a primeira lei e com o conceito de energia interna.
    
3. Podemos classificar a irreversibilidade em graus ou até mesmo associar um valor numérico à mesma.
    
4. Este valor numérico está de alguma forma relacionado ao trabalho W' como definido anteriormente ou, ainda, e de maneira mais simples, está de alguma forma relacionado ao número de etapas em que a transformação ocorreu.
    
5. Tudo nos leva a crer que, para um mesmo estado inicial e final, o processo será tanto mais irreversível quanto menor o número N de etapas; e estará tanto mais próximo da reversibilidade quanto maior o número N de etapas, chegando-se à reversibilidade na situação limite em que o número de etapas N é infinito.

O que nos falta para chegarmos à entropia? Diria, por ora, que dá para perceber a existência de alguma coisa no ar e a nos dizer que deve existir um conceito muito importante por trás da dupla reversibilidade/irreversibilidade. No entanto, até agora falamos em transformações de estado e o que percebemos sujeitar-se à mensuração relaciona-se à transformação em si, não sendo uma propriedade inerente a quaisquer dos estados do sistema que sofre a transformação (o gás). Em outras palavras, passamos de "um estado inicial" a "um mesmo estado final" por processos vários, "medidos" por uma variável W' (= Mgh, Mgh/2, Mgh/3, Mgh/4 ...) ou N (=1, 2, 3, 4 ...). Por outro lado, W' relaciona-se a uma medida relacionada aos processos de "ida" e "volta" somados, ou seja, relaciona-se a quanto de capacidade de realizar trabalho o universo deve perder para que o sistema gás retorne a um estado inicial, bem definido, após passar por um outro estado (o estado final da etapa de "ida" do processo) também bem definido. Qualquer tentativa de definir W' como uma propriedade do estado final, por exemplo, esbarraria na necessidade de termos que fixar o estado inicial como de referência, ou padrão. Pelo visto, algumas considerações estão faltando para que possamos caracterizar esta propriedade que "está no ar" (a entropia ou qualquer outra equivalente) com rigor e praticidade.

É importante entender bem o conteúdo do parágrafo anterior, de maneira que vou expô-lo sob um prisma um pouco diverso. Por um lado cheguei a dizer que W' é útil para caracterizarmos o grau de irrreversibilidade da transformação, mas não para caracterizarmos qualquer possível estado do sistema gás. Por outro disse que, sob restrições, poderíamos escolher um determinado W' para chegarmos a alguma propriedade importante de um dos estados (o final no caso), em relação a outro (o inicial no caso), do gás que sofre a transformação. Mas se existem infinitos W's, qual deles escolher? Aquele que está mais próximo da irreversibilidade total (com N = 1)? Qualquer outro, com N diferente de 1? Ou aquele que está mais próximo da reversibilidade ideal (com N = infinito)? Muito provavelmente iríamos escolher ou N = 1 ou N = infinito, jamais um valor intermediário e/ou aleatório. Por motivos de ordem histórica, a escolha feita foi aquela em que N = infinito, ou seja, a situação em que a transformação é totalmente reversível, "a menos de um infinitésimo".

Embora, como já disse, W' não seja a melhor grandeza a caracterizar a reversibilidade/irreversibilidade, ele desempenha um papel didático de grande valor, para que possamos chegar a entender a entropia. Por outro lado, é comum encontrarmos, nos textos de termodinâmica, as expressões "rev" ou "irrev", em geral em tipo de letra menor e rebaixadas no texto, associadas a determinadas grandezas. Por exemplo, é comum o encontro de Q_rev ou Q_irrev (Q seria o calor transferido de um sistema a outro numa transformação "rev" ou "irrev", respectivamente). O significado de "rev" ou "irrev" assim apresentados tem muito a ver, respectivamente, com o N = infinito ou o N = 1, acima apresentados. Consequentemente, e pelo mesmo motivo, poderíamos dizer que W'_irrev seria numericamente igual à capacidade de realizar trabalho perdida pelo universo numa transformação "totalmente" irreversível (totalmente deve ser aqui interpretado como o grau máximo de irreversibilidade para o caso considerado, qual seja, fixados os estados inicial e final).

Rigorosamente falando, W' = Mgh, com N = 1 (figura 1), não representa uma medida da "irreversibilidade total" (W'_irrev) a menos que pretendamos restringir nosso estudo ao "modelo" de transformações apresentadas nas figuras 1 a 3. Com efeito, poderíamos chegar ao estado final retirando não apenas a massa M mas também a massa m de cima do êmbolo. Chegaríamos então, por processo semelhante aos até aqui adotados, a calcular, agora sim, W'_irrev = (M + m)gh. Pergunto: Como chegar ao mesmo estado final sem o auxílio da massa m? Muito simples: coloque uma presilha nas paredes do recipiente de tal maneira que o êmbolo seja bruscamente freado assim que atingir a altura desejada (a mesma que atingiria caso conservássemos a massa m em cima do êmbolo, ou seja, h). Neste caso devemos supor a idealidade relacionada à massa desprezível do êmbolo. O processo seria equivalente à chamada expansão no vácuo.

É importante perceber que Q_rev, por exemplo (ou qualquer outra grandeza "rev" ou "irrev", como W_irrev), aparece em fórmulas que definem propriedades de estado. Se for o caso, deve-se entender que a propriedade assim definida a partir de Q_rev (por exemplo, a entropia) está expressa na notação "Δ" (delta grego maiúsculo), ou seja, representando a diferença do valor da propriedade entre dois estados; e tal que, ao passar de um estado a outro por um "caminho reversível", a troca de calor com o universo restante é igual a Q_rev.

As expressões que contém grandezas "rev" (ou mesmo "irrev") nos dizem que a maneira apropriada de "medirmos" a outra grandeza apresentada (aquela definida pela expressão correspondente), e em notação "Δ", seria através da determinação laboratorial da grandeza "rev" (ou "irrev"). Ou seja, deveríamos seguir um "caminho reversível" (ou "totalmente irreversível", para o caso "irrev"). Em geral é muito difícil encontrar, em livros didáticos, grandezas "irrev", a menos que o autor seja um seguidor de Prigogine, um famoso estudioso do assunto, deste século, e que enfatizou a importância dos processos "totalmente irreversíveis".

Resumindo, o importante é perceber que os estados finais dos gases que sofreram as transformações apresentadas nas figuras 1 e 2 são idênticos e portanto suas propriedades de estado devem coincidir (incluindo a energia interna, a entropia ou outra equivalente, além de p, V e T). Não obstante, passaram por graus distintos de irreversibilidade, como vimos, o que se caracterizou por W's diferentes. As grandezas "rev" ou "irrev" são artifícios operacionais a nos mostrarem o caminho a ser seguido se quisermos realmente "medir" a grandeza relacionada. Ou seja, entre um estado e outro, Q somente será igual a Q_rev se o processo em estudo for reversível, caso contrário Q_rev será um valor teórico sem relação com o calor efetivamente trocado entre o sistema e a fonte. Não obstante, ainda que o calor efetivamente trocado seja Q e não Q_rev, dizemos que a entropia está relacionada a Q_rev, o que com grande frequência gera confusão entre os estudantes.

 
Ü    Índice do Diálogo
Próximas Mensagens    Þ

DHTML Menu By Milonic JavaScript