Continuação da mensagem 17:

Entalpia H e Energia Livre G de Gibbs

Em 05/12/99, na mensagem 03 desta série, André escreveu:

Porque na química nós estudamos entalpia e na física não?

O estudo da entalpia H surge durante a análise da primeira lei. Trata-se de outro "construto de alto nível" e, neste caso, a relacionar a energia interna com o produto pV, qual seja,

H = E + pV.                (eq 1)

A entalpia assume importância, dentre outras condições, quando do estudo de sistemas a pressão e volume constante. Em virtude de os químicos estudarem, com relativa frequência, soluções com volume constante e a ocorrerem na pressão atmosférica ou, então, reações químicas que ocorrem em tais soluções, provavelmente resida aí um dos motivos de sua preferência por H em substituição à energia interna E. Com efeito, facilmente demonstra-se que em tais condições (p e V constantes) temos

dH = dE.

É suficiente derivar a equação 1 (eq 1) acima, obtendo-se

dH = dE + pdV + Vdp,

e observar que, para as condições assinaladas, dV = dp = 0.

Se substituirmos em eq 1 o valor de E dado pela equação utilizada na mensagem 17 para definir a entropia, qual seja,

E = A + TS

chegamos a

H = A + TS + pV

ou, o que é o mesmo,

H - TS = A + pV.                (eq 2)

Pela observação das equações 1 e 2 (eq 1 e eq 2) podemos pensar, raciocinando por analogia, numa outra propriedade termodinâmica G a relacionar-se com a energia livre A de Hemholtz, da mesma forma que a entalpia relaciona-se com a energia interna E, ou seja,

G = A + pV                (eq 3)

e, de (eq 2),

G = H - TS.                (eq 4)

Com efeito, de (eq 3) obtemos, para p e V constantes, dG = dA.

G, frequentemente definido pela expressão dada em eq 4, nada mais é do que a energia livre de Gibbs, importantíssima em físico-química, termodinâmica química, bioquímica e biofísica. Lembro ainda que nestas disciplinas surgem variáveis outras graças a variações de concentração de componentes pertencentes ao sistema como, por exemplo, o número de moles dos participantes das reações químicas. Surge então a necessidade da conceituação dos "potenciais químicos", intimamente relacionados à energia livre de Gibbs.

Resumindo, as equações fundamentais da termodinâmica a relacionarem seus diversos construtos de alto nível são:

H = E + pV                (eq 5)
A = E - TS                (eq 6)
G = H - TS                (eq 7)

Estas são frequentemente referidas como equações de definição de H, A e G respectivamente ("E" é definido a partir da primeira lei da termodinâmica e "S" a partir da segunda lei por uma via diversa da apresentada nesta série). A termodinâmica propriamente dita começa após definirmos suas variáveis Assim sendo, neste ensaio simplesmente procurei colocar o net-amigo que acompanhou as postagens de posse dos fundamentos para que possa iniciar o estudo da termodinâmica sem grandes dificuldades.

Para o físico todas essas grandezas (H, E, A, S e G) são importantes e ele irá valorizar uma ou outra na dependência do problema de interesse momentâneo, pois temos mais grandezas do que o número necessário para as definições dos estados dos sistemas estudados. Graças às relações mostradas em eq 5 a eq 7, é sempre possível mudar o enfoque à medida da necessidade. Por motivos óbvios, alguns dos quais a serem apontados nas próximas mensagens (vide mensagem 32 e seguintes), energia interna E e entropia S destacam-se frente as outras, sem que isso signifique uma depreciação das demais por parte do físico.

As mensagens 19 a 31 e 33 a 41 foram postadas na Ciencialist e refletem uma discussão paralela que se seguiu após as mensagens 01 a 18 terem sido apresentadas no eCC. Como o tema evoluiu em outra direção, estas mensagens são apresentadas após a mensagem 44.

Continuação da mensagem 18:

Generalizando os Conceitos Termodinâmicos

Retornando às questões primeiras desta série, verificamos que na mensagem 03 de 05/12/99, André escreveu:

André: O que me deixa mais confuso nessa tal de entropia é a sua equivalência aos fenômenos que ocorrem no nosso dia-a-dia.

Realmente, isto é um fato. Nota-se que os conceitos termodinâmicos extrapolam as pretensões pedagógicas, destinadas a explicarem o que ocorre no laboratório. Abandonam o papel em que foram impressos, nos livros didáticos e, muito além de simplesmente sustentar a tecnologia, passam a ser por nós vivenciados, chegando mesmo a ganhar uma conotação popular nem sempre bem explicada mas, ainda assim, repetida a exaustão.

A generalidade da termodinâmica passa desapercebida por muitos dentre aqueles que apenas cumprem créditos básicos da graduação. E fica sempre aquela dúvida, a ser expressa no seguinte questionamento: Com que autoridade podemos tabular uma série de fórmulas e/ou afirmações surgidas, por exemplo, ao manusearmos sistemas gasosos a levantarem ou baixarem massas, em seus contatos com fontes quentes e frias, e daí aplicá-las aos demais fenômenos observados no dia-a-dia?

Respondendo, diria: O alcance da termodinâmica não se restringe ao estudo dos gases. Aliás, seria possível definirmos todas as propriedades termodinâmicas enfatizadas nesta série de mensagens (E, S, A, H e G) sem fazermos apelo algum ao estudo dos gases. Pressão p e volume V, como vimos, foram utilizados meramente para que pudéssemos expressar, e/ou dotar de características mensuráveis, a energia em trânsito, a vaguear entre um sistema e outro e conhecida como trabalho; ou então para que pudéssemos entender até que ponto p e V relacionam-se com as propriedades termodinâmicas, quando realmente se fazem presentes (gases, soluções, misturas, etc.).

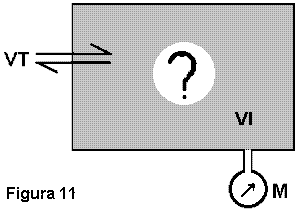A termodinâmica estuda uma infinidade de sistemas físicos, isolados ou em interação e que se prestam a serem descritos através de dois tipos de variáveis: as variáveis internas (VI), características instantâneas do estado do sistema e as variáveis de transporte (VT), a refletirem o que atravessa as fronteiras do sistema considerado, entre um estado e outro (figura 11).

As variáveis internas (VI) subdividem-se em dois tipos:

1. Aquelas próprias a cada modelo estudado (por exemplo, p, V e T se o modelo for um gás). Normalmente são de conceituação não muito laboriosa e passíveis de mensuração direta (o aparelho de medida dessas variáveis está genericamente representado por M na figura 11 e poderia ser um manômetro, uma régua, um termômetro, etc.); com grande frequência prestam-se a estimativas subjetivas, via órgãos dos sentidos.
    
2. Aquelas comuns a todos os modelos estudados e a constituírem as propriedades termodinâmicas propriamente ditas dos sistemas. Via de regra são construtos de alto nível (E, S, A, etc.) e a diferença de valores que assumem entre um estado e outro está relacionada de alguma maneira ao que atravessou (ou seja, as VT's) ou ao que poderia ter atravessado, em condições especiais (vias reversíveis, por exemplo), as fronteiras do sistema, entre um estado e outro. É pela observação dessas propriedades que verificamos o quanto a termodinâmica é abrangente e a incorporar a totalidade dos processos naturais em evolução de um estado para outro.

As variáveis de transporte (VT) são, em geral, calor e trabalho (energia em trânsito), podendo-se pensar, também, no transporte de massas (em geral isso é feito na disciplina "Fenômenos de Transporte", que apresenta muitos capítulos afinados com a termodinâmica). Quase sempre são estimadas graças a alterações observadas no meio exterior ao sistema estudado, como o levantamento de um peso, ou o esfriamento ou aquecimento de uma solução em contato com o sistema ou, ainda, uma variação na concentração de determinada substância desta solução. É graças a propriedades como estas que podemos verificar o que há de comum entre processos tão distintos como a expansão de um gás, a queda livre, o transporte de calor entre fontes térmicas, a corrente elétrica que se estabelece entre corpos com potenciais elétricos diferentes, as reações químicas, etc. E o que há de comum muitas vezes relaciona-se intimamente ao grau de irreversibilidade observado, qual seja, a marca que o processo deixa no "resto do Universo". E esta marca pode sempre ser relacionada a algo equivalente ao abaixamento de massas num campo gravitacional ou, dito de outra forma, podemos dizer que o universo em apreço sofreu redução na capacidade de realizar trabalho.

Vamos considerar três casos simples de processos irreversíveis para que fique nítida esta equivalência. Deixarei então como tema, a ser pensado, a verificação de uma possível equivalência entre os seguintes processos:

1. Queda de um corpo de uma altura h seguida de choque totalmente inelástico com o solo (figura 12, onde Q representa o calor liberado no processo para o meio ambiente);
    
2. Transporte irreversível de calor entre uma fonte quente, à temperatura T1 e uma fonte fria, à temperatura T2 (figura 13). A fonte fria pode ser pensada como sendo o meio ambiente;
    
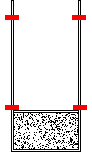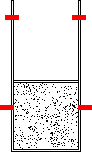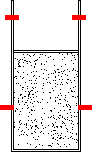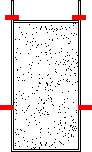
3. Expansão irreversível de um gás de um volume Vi até um volume Vf, em uma única etapa e num recipiente com paredes adiabáticas e, portanto, sem efetuar trocas de calor com o meio ambiente (figura 14).

Figura 12		Figura 13		Figura 14

Até a próxima (mensagem 42, de 261299) e, enquanto isso, convido a todos para que acompanhem, através de meu Web Site, o rumo totalmente diferente que o tema tomou na Ciencialist (mensagens 19 a 31, de 20/12/99 até hoje, 22/12/99) onde discutiu-se, dentre outros assuntos, o problema da expansão do Universo e sua possível relação com o aumento da entropia.

Continuação da mensagem 32:

Espontaneidade e Evolução para o Equilíbrio

Uma dentre as inúmeras maneiras de enunciarmos a segunda lei da termodinâmica relaciona-se à tendência de sistemas, não vinculados a restrições, evoluírem para um estado de "equilíbrio térmico" (uma restrição digna de nota seria aquela apresentada por sistemas compartimentalizados às custas de membranas adiabáticas). Obtido esse "equilíbrio térmico", a propriedade "macroscópica" temperatura assume valores iguais em toda a extensão do sistema. Assim, se num dado instante tivermos duas regiões a diferentes temperaturas, T₁ e T₂, espera-se que o sistema caminhe espontaneamente para uma condição de equilíbrio tal que possa vir a ser caracterizado por apenas uma temperatura T, situada entre T₁ e T₂.

No parágrafo anterior ficaram implícitos alguns questionamentos e alguns conceitos importantes:

1. Em que condições podemos dizer que um sistema encontra-se em equilíbrio?
    
2. Qual a distinção entre "equilíbrio entre sistemas" e "sistema em equilíbrio"?
    
3. Espontaneidade e evolução para o equilíbrio seriam a mesma coisa?
    
4. A evolução de um estado para outro, implica, sob o ponto de vista da termodinâmica, na admissão da existência de um instante "anterior" e um instante "posterior". Que dizer do intervalo de tempo entre um instante e o outro, ou seja, da duração do processo? Quando dizemos que a duração de um processo é irrelevante para a termodinâmica... Seria isso equivalente a dizermos que a termodinâmica ignora a transformação em si?
    
5. Os inúmeros enunciados, textualmente diferentes, da segunda lei da termodinâmica, são realmente equivalentes?
    
6. Se a termodinâmica clássica trabalha com propriedades macroscópicas... Poderíamos estender suas conclusões ao microcosmos? Poderíamos avaliar a temperatura de uma molécula?

Levantados os problemas, vamos comentá-los resumidamente, o suficiente para que possamos "aceitá-los numa boa" e, assim sendo, para que possamos prosseguir com nossas "encucações".

Direi então, com respeito à questão 1, que "um sistema atingiu o estado de equilíbrio quando não revela nenhuma tendência para uma ulterior variação de suas propriedades com o tempo". Este conceito parece-me constar do livro de físico-química do Moore, ainda que no momento não esteja de posse do mesmo. A esse respeito, assim me manifestei há alguns anos:

Não há como confundir, através desta definição, equilíbrio com estado estacionário, se é que o leitor está acostumado com este último termo. Se não estiver, um exemplo simples poderá ajudá-lo. Imagine um tanque com água até determinado nível. Se o nível permanecer constante, no decorrer do tempo, isto pode se dever a dois fatores: a tampa inferior do tanque está fechada; ou a torneira está aberta de tal forma que seu fluxo iguale a vazão, ou o que vai para o ralo. No primeiro caso, o sistema está em equilíbrio; no segundo, em estado estacionário. Notem a tendência para uma ulterior variação das propriedades com o tempo, neste segundo caso: o ralo ou a canulação podem entupir; a caixa d'água pode se esvaziar, etc.

Que dizer então de "equilíbrio entre sistemas" (questão 2). Ora, diferentemente do caso anterior, estamos aqui trabalhando com pelo menos dois sistemas; logo, não há como confundir os termos. De alguma forma, vem-nos a idéia de confronto entre sistemas, bem como da possibilidade de transporte líquido (no sentido contábil do termo) de alguma coisa, de um dos sistemas para o outro, caso não exista o equilíbrio. Por outro lado, pode-se pensar, num sistema único, como estando subdividido em compartimentos e, neste caso, estando ou não o sistema em equilíbrio, poderíamos também conjeturar sobre se os possíveis compartimentos, analisados dois a dois, estariam ou não em equilíbrio entre si.

O princípio do equilíbrio entre sistemas nada mais é do que uma generalização do princípio do equilíbrio térmico, ou lei zero da termodinâmica, e poderia ser enunciado como: Dois sistemas em equilíbrio com um terceiro através de um mesmo tipo de confronto, estão em equilíbrio entre si, através de pelo menos um tipo de confronto. Exemplos de confrontos:

1. visual (tamanho, forma, etc.);
2. através de alavancas ou balanças;
3. mensuráveis através de termômetros;
4. confronto chave-fechadura, etc.

A cada tipo de confronto é possível definir uma grandeza representativa do mesmo e atribuir padrões ou escalas de medidas (ex.: comprimento, cor, massa, temperatura, etc.). Por outro lado, os sistemas em equilíbrio estão sujeitos a vários princípios como, por exemplo, o princípio da continuidade, o princípio de Le Chatelier, etc. (Uma breve introdução, de minha autoria, aos princípios que regem os fenômenos naturais, pode ser encontrada em Eletromagnetismo e Relatividade).

Que dizer da espontaneidade e/ou da evolução para o equilíbrio (questões 3 e 4)? Ora, aqui estamos já entrando na essência das transformações, a justificarem o estudo da termodinâmica. Por paradoxal que possa parecer, a termodinâmica, ao valorizar, através das propriedades de estado, o "antes" (estado inicial) e o "depois" (estado final), deixando totalmente à margem o "durante" (o processo em si), é, sem dúvida alguma, o capítulo da física que mais profundamente envolve-se com as transformações em si (e daí a expressão dinâmica). O descaso para com o "durante" é de natureza puramente operacional, qual seja, relativo aos valores assumidos pelas propriedades "durante" o processo. A termodinâmica não nega a existência do processo; simplesmente recusa-se a fazer conjecturas sobre valores intermediários de variáveis que sabe, de antemão, não corresponderem à realidade (Qual é a temperatura de um gás durante sua expansão???); a menos que o processo seja reversível, mas, nesse caso, temos a chamada condição de quasi-equilíbrio onde "antes", "durante" e "depois" praticamente se sobrepõem e as propriedades de estado estão fixas, a menos de infinitésimos.

Tanto é verdade que a essência da termodinâmica vincula-se às transformações em si, e não aos estados de equilíbrio inicial e final, que as suas duas leis fundamentais, relacionam-se às transformações. A segunda lei, por exemplo, refere-se à "evolução" dos sistemas para um estado de equilíbrio e não à manutenção de um estado de equilíbrio. Uma das maneiras clássicas de enunciá-la, e a denunciar esse comprometimento, seria: O calor passa de um corpo quente para um corpo frio, não ocorrendo o inverso.

Além da passagem de calor de um corpo quente para um corpo frio, existe uma infinidade de outros processos a nos denunciarem sua espontaneidade. Pensemos, por exemplo, no que ocorre num campo gravitacional. Se dissermos: Num campo gravitacional, um corpo que cai espontaneamente, não sobe espontaneamente (figura 12)... Até que ponto poderíamos utilizar esta afirmação raciocinando termodinamicamente? Seria equivalente a dizer que o calor passa de um corpo quente para um corpo frio, não ocorrendo o inverso (figura 13)?

O que tem a ver a espontaneidade da queda de corpos em campos gravitacionais com a termodinâmica? Por outro lado, sabemos também que: Num campo gravitacional dotado de atmosfera, um corpo que sobe espontaneamente, não cai espontaneamente. Seria essa uma nova maneira atípica de enunciarmos a segunda lei da termodinâmica?

Voltemos agora para os gases: Numa atmosfera rarefeita, os gases se expandem, não ocorrendo o inverso (figura 14).

O que há de comum em todas essas afirmações? Seriam elas equivalentes? (questão 5, acima) Se negarmos uma destas afirmações, estaremos negando as demais?

Exemplos de Processos Irreversíveis
Figura 12		Figura 13		Figura 14

Pois o segredo do segundo princípio da termodinâmica está na equivalência dessas afirmações e reside não na fixação da direção de um processo qualquer mas na afirmação de que na ausência de agentes externos, qualquer processo segue uma direção natural: não importa para que lado ou em que sentido, sabendo-se, no entanto, que uma vez estabelecido ou determinado o sentido, este será reconhecidamente imutável. Dito de outra forma, o que o segundo princípio da termodinâmica nos garante é que os fenômenos naturais são irreversíveis ou, então, que existe, nos mesmos, uma direção espontânea a ser seguida e tal que, sistemas isolados ou estão em equilíbrio ou estão evoluindo para uma condição de equilíbrio.

Porque então chamarmos a ciência que estuda a evolução natural dos processos pelo nome de termodinâmica? O que tem o calor, ou a energia térmica, a ver com a evolução fenomenológica da natureza?

Como veremos na próxima mensagem, o calor, mesmo quando não participa do processo em si, desempenha um papel central e a nos mostrar como processos tão diferentes se equivalem. Aliás, dizer que o calor não participa do processo (por exemplo, numa expansão adiabática e expontânea de um gás) não seria uma afirmação muito condizente com a filosofia termodinâmica pois a termodinâmica "não mede" nada do que ocorre "durante" o processo; logo se, de alguma forma, "o sistema trocar calor consigo mesmo", isso estará além do escopo da termodinâmica.

Quanto à questão 6, o que poderia ser dito aqui já foi tema do diálogo que travei com o Neville na Ciencialist e está publicado nesta série nas mensagens 31, 33, 39 e 41.

Continuação da mensagem 42:

Máquinas Térmicas

Como vimos, em mensagens anteriores, é possível um sistema, por exemplo, um gás, produzir trabalho, extraindo calor de uma fonte quente. Se o processo for cíclico, como aquele representado na figura 8, e contínuo, teremos uma máquina térmica; e, pelo que sabemos, se o sistema for um gás, o trabalho máximo 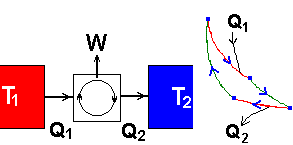produzido em cada ciclo (W_max = W_rev), quando representado através de unidades convenientes, iguala a área delimitada pelo ciclo, num gráfico pV. A figura 15, ao lado, representa um tal processo:

Neste caso o gás recebe uma quantidade de calor Q₁, da fonte à temperatura T₁, e cede a quantidade de calor Q₂ à fonte à temperatura T₂. Nas adiabáticas (linhas verdes, na figura) sabemos que não há trocas de calor, pois o gás fica confinado entre paredes que impedem o estabelecimento de equilíbrio térmico com o meio próximo.

Pela primeira lei da termodinâmica sabemos que W = Q₁ + Q₂ (Q é positivo quando o gás recebe calor e negativo no caso contrário). Uma pergunta que nos vem à mente é: Seria possível Q₂ ser igual a zero? É evidente que neste caso o conjunto seria bastante simplificado, não havendo necessidade da fonte à temperatura T₂. E a fonte à temperatura T₁ poderia ser o meio ambiente. A figura 16 ilustra tais simplificações:

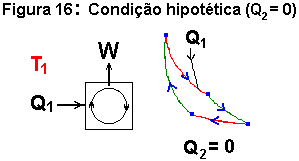Suponhamos que a resposta à pergunta fosse afirmativa. Pensemos agora na queda de um objeto, como mostrado na figura 12, e vamos aceitar o processo, aí representado, como irreversível e a caracterizar a segunda lei. Poderíamos então utilizar a máquina da figura 16 para elevar o objeto que caiu. O trabalho necessário a ser produzido na máquina iguala o calor Q liberado pelo objeto ao se chocar com o solo (primeira lei); mas este trabalho, fosse a condição hipotética da figura 16 verdadeira, deveria ser igual a Q₁ (também pela primeira lei). Consequentemente, Q = Q₁. Logo, ao término do processo, o saldo em energia térmica recebido pelo meio ambiente é igual a zero; e o objeto retorna ao seu ponto de partida. Como o gás também retornou ao seu valor inicial (processo cíclico), a conclusão é que o processo foi totalmente revertido, a contrariar a suposição aceita inicialmente.

Podemos então, de posse desses argumentos, afirmar: É impossível um sistema trabalhando ciclicamente, receber calor de uma fonte térmica e apresentar, como único efeito, a realização de trabalho. Ou seja, segundo essa afirmação, a máquina térmica representada na figura 16 (com Q₂ = 0) "não deveria existir. Essa proposição (em itálico) é a mais frequentemente encontrada como "segunda lei da termodinâmica".

Utilizando a expansão irreversível de um gás, como mostrado na figura 14, chegaríamos, por raciocínio semelhante, à mesma conclusão. Ou seja, o gás, para retornar à condição primitiva, poderia sofrer uma contração reversível, cedendo, no processo, uma quantidade de calor Q ao meio ambiente (caso contrário, se o processo fosse adiabático, pela primeira lei o gás não retornaria ao estado primitivo). O trabalho (= Q pela primeira lei) para promover essa 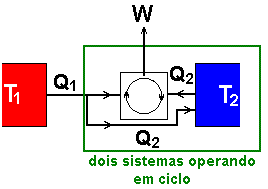contração "poderia" vir da máquina hipotética representada na figura 16 a qual extrairia do meio ambiente (fonte) uma quantidade de calor Q₁ = W = Q. E como Q₁ = Q, o saldo energético do meio ambiente iguala-se a zero e o processo acaba por ser revertido, o que contraria a hipótese inicial (expansão "irreversível").

Seria possível termos, na figura 15, Q₂ > 0? Examine a figura 17 e conclua que neste caso poderíamos juntar a fonte T₂ e o gás como um único sistema cíclico e retornaríamos à condição hipotética da figura 16, a qual não satisfaz a hipótese da irreversibilidade dos fenômenos naturais. Repare que a fonte T₂ cede Q₂ numa etapa e recebe Q₂ em outra, trabalhando portanto em regime cíclico, tal e qual o gás.

Que dizer então da figura 13 ou da afirmação correspondente: O calor passa de um corpo quente para um corpo frio, não ocorrendo o inverso. Se fosse possível uma quantidade mensurável de calor Q passar espontaneamente 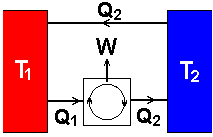de uma fonte fria à temperatura T₂ para uma fonte quente à temperatura T₁, poderíamos acoplar as duas fontes a um sistema cíclico capaz de realizar trabalho, como aquele representado na figura 15 (agora não mais a máquina hipotética da figura 16). Ao igualarmos Q₂ a Q (supondo que a máquina possa trabalhar no ritmo que quisermos), teremos a situação representada na figura 18.

Tudo se passa como se o sistema, trabalhando em processo cíclico, recebesse a quantidade de calor Q₁ - Q₂ apenas de uma das fontes (T₁), o que novamente contraria qualquer das outras hipóteses aceitas como que a representarem textualmente a segunda lei da termodinâmica. Percebemos então que, ao contrariarmos a irreversibilidade proposta para o transporte de calor, estaremos concomitantemente contrariando as demais irreversibilidades vistas.

Espero ter deixado clara a equivalência entre os vários enunciados da segunda lei da termodinâmica, bem como o relacionamento implícito entre a segunda lei, a irreversibilidade e a espontaneidade. E por falar em espontaneidade, podemos agora concluir a resposta à seguinte pergunta do André, constante da mensagem 3:

O que determina um fenômeno ser ou não espontâneo?

A termodinâmica é uma teoria fenomenológica, não indo às causas últimas dos fenômenos. A espontaneidade é o seu ponto de partida: observa-se a existência, na natureza, de uma direção preferencial para a ocorrência dos fenômenos e, ao constatarem esta preferência, os estudiosos do assunto concluíram pela observância da segunda lei. Porque em determinadas condições um corpo cai e não sobe espontaneamente? Ora, quem vai nos responder a essa questão não é a termodinâmica, pois forças e campos (causas imediatas) não pertencem ao seu domínio. Porque um gás se expande? Não há como respondermos a essa pergunta sem entrarmos no representacionismo, substituindo a natureza flúida do gás por sua natureza molecular; mas aí estaríamos entrando no domínio de teorias outras, tais como a mecânica estatística ou mecânica quântica. Porque o calor passa de um corpo quente para um corpo frio, não ocorrendo o inverso? Não há como responder a essa pergunta com o modelo termodinâmico, a não ser dizendo que, "se ocorresse o inverso", a termodinâmica ou não existiria ou seria algo totalmente diferente; e o Universo também!

Na mensagem 3 encontramos também a seguinte pergunta:

Será que qualquer tipo de fenômeno ou ação é reversível ou irreversível?

Aparentemente, todos os sistemas naturais ou estão em equilíbrio ou então estão evoluindo para um estado de equilíbrio, seguindo uma via irreversível. O estado estacionário assemelha-se a um equilíbrio quando visualizado com "lente de pequeno aumento". No entanto, ao ampliarmos o objeto de estudo, englobando as vizinhanças do sistema aparentemente em equilíbrio, verificamos que atingiremos uma dimensão na qual perceberemos que o sistema ampliado está, de alguma forma, evoluindo para um estado de equilíbrio.

Da mesma forma que a termodinâmica não vai às causas da espontaneidade, ela também não explora, sob esse aspecto, a irreversibilidade. Em outros domínios da física chegamos a reconhecer que a irreversibilidade deve-se a fenômenos como atrito, inelasticidade, viscosidade, resistência elétrica, etc. Até mesmo nesses domínios, os agentes causais são, em última instância, praticamente ignorados. As teorias microcósmicas (mecânica estatística e mecânica quântica) não conseguiram ainda explicar tais fenômenos, o que parece-me ser fundamental para que um dia possamos entender o porquê da irreversibilidade.

Recentemente propus uma teoria representacional e, de certa forma, interligada à minha teoria sobre os elétrons, na qual explico a irreversibilidade apelando, sempre que houver atrito ou outro "agente de irreversibilidade", para a emissão de uma partícula elementar a que dei o nome de entropino (muito provavelmente seriam os próprios neutrinos da física moderna). Consigo explicar a irreversibilidade como um processo local e não obrigatoriamente universal. O Universo, como um todo, comportaria a reversibilidade e, desta forma, pelo menos em teoria, comportaria a eternidade, sem que houvesse a necessidade de invertermos suas leis, como propoem algumas das teorias "iô-iô" de expansão-contração. Curiosamente, ainda que, com essa idéia, a segunda lei perca muito de seu conteúdo original, ela não chega a ser substancialmente modificada, quando analisada do ponto de vista macroscópico; não obstante, a teoria propõe uma adaptação da primeira lei, não sob o ponto de vista termodinâmico propriamente dito, mas sob o aspecto representacional. Ou refutamos a idéia a dizer que a primeira lei retrata o princípio da conservação da energia ou então teremos que reformular o conceito de equivalência entre calor e trabalho; ou ainda, ambos. Posto que os entropinos (neutrinos?) também transportam energia, sem entrarem contabilmente na soma calor + trabalho.

A teoria está descrita em Variáveis escondidas e a termodinâmica (Observação: trata-se de uma teoria alternativa e ainda não aceita pela comunidade científica; se alguém estiver se preparando para um concurso público como, por ex., vestibular, sugiro que ignore este e o parágrafo anterior).

Continuação da mensagem 43:

A função dos paradoxos nas ciências naturais

Paradoxo, dizem os dicionários, nada mais é do que um "conceito a contrariar o que nos parece evidente"; ou então, uma "afirmação que vai de encontro a sistemas ou pressupostos que se impuseram, como incontestáveis, ao pensamento". Sua utilização, em ciência, é muito comum e presta-se, em determinados casos, a falsear ou mostrar a inconsistência de um determinado modelo teórico. Por outro lado, "resolver o paradoxo" nada mais é do que destruir a argumentação, nele contida, pela utilização de dados inerentes ao modelo contrariado; demonstra-se, desta forma, a inconsistência do paradoxo, o que, sob certos aspectos, corrobora o modelo teórico. Diferentemente das hipóteses falseadoras, sua resolução, via de regra, não lança mão da experimentação, razão pela qual é quase sempre apresentado e/ou resolvido por cientistas teóricos e/ou teorizadores.

Um paradoxo não resolvido enfraquece a teoria alvo, podendo, em casos excepcionais, servir como motivo para o seu abandono pela comunidade científica; mais comumente, serve como apelo para que se procure por variáveis escondidas, o que não costuma ser bem visto pelos adeptos da teoria, pois revela a fragilidade de seu núcleo "imutável" (conceitos já definitivamente aceitos e tidos como imutáveis) bem como a necessidade de uma profunda revisão e/ou reformulação das hipóteses.

Nem sempre o paradoxo, ao ser resolvido, mostra-se inconsistente. Não raramente, chama a atenção para algo inerente à teoria porém que não estava sendo devidamente valorizado, a ponto de ter gerado o paradoxo. Refiro-me a situações em que o paradoxo foi resolvido sem a necessidade da incorporação de hipóteses ad hoc à teoria. A introdução de hipóteses ad hoc é prática comum nos chamados períodos de ciência normal nos quais, segundo Thomas Kuhn, a dogmatização, de forma lamentável, chega a ser tolerada, quando não defendida. Não se deve confundir "procura" de variáveis escondidas, o que pode resultar na "incorporação" de novas hipóteses, com "aceitação" pura e simples de novas hipóteses: a primeira apóia-se na experimentação e sujeita-se ao método científico; a segunda nada mais é do que um artifício a "burlar" a falseabilidade.

No século XX, o paradoxo mais comentado, sem dúvida alguma, foi o paradoxo dos gêmeos, também conhecido como paradoxo dos relógios, a pleitear a inconsistência da teoria da relatividade de Einstein. Sob certos aspectos, podemos também dizer que a experiência EPR, de pensamento, retrata outro paradoxo, agora a contradizer a mecânica quântica. Deixadas as paixões de lado, nenhum dos dois paradoxos foi ainda resolvido, e é suficiente perpassar os olhos pelos grupos de discussão internacionais da Usenet para verificar quão grande é o número de acadêmicos que, alheios ao dogmatismo que se apossou da física no século XX, dispõem-se a discutir o que, para os dogmáticos adeptos de Thomas Kuhn, não comportaria discussão alguma.

Paradoxos menores pipocam aqui ou acolá, e não posso deixar de citar um paradoxo que construí há mais de cinco anos (Einstein Equivalence Principle is wrong?), tentando mostrar a inconsistência do princípio da equivalência de Einstein. Recebi, em 1998, algumas críticas, no newsgroup sci.physics.relativity, sobressaindo, dentre estas, a argumentação do Paul Andersen que, se não convincente, traz à tona idéias novas, ainda que ad hoc. Refiz a argumentação (Einstein-Faraday's Elevator) e estou, há quase 2 anos, sem receber crítica alguma, nem dos frequentadores dos newsgroups onde a reformulação foi postada (sci.physics.relativity e alt.sci.physics.new-theories, além de outros nacionais), nem dos leitores do meu Web que, neste período, recebeu um número razoável de visitantes. Comento alguma coisa a respeito em "Diálogos Usenet 06" (vide item 7).

Vamos agora ao que interessa: O paradoxo, referido na mensagem 13, foi apresentado aos newsgroups sci.physics.relativity, alt.sci.physics.new-theories, uol.ciencia, brasil.ciencia.fisica e pt.ciencia.geral e, se não me falha a memória, aqui na lista física, nos seguintes termos:

Sejam dois compartimentos, 1 e 2, separados um do outro por uma membrana sólida, adiabática e móvel (figura 5, reproduzida ao lado - clique na figura para ampliá-la). Suponhamos que suas pressões sejam, respectivamente, p₁ e p₂ e tais que p₁ > p₂.

Abandonado sobre si mesmo, o sistema evoluirá para uma situação de equilíbrio tal que p₁ = p₂. Consoante notação expressa na maioria dos livros de físico-química (por exemplo, Castellan, para o qual

                W = p_opdV,

onde p_op = pressão de oposição), teremos:

                W₂ = Trabalho recebido pelo sistema 2 = p₁dV

                W₁ = Trabalho exercido pelo sistema 1 = p₂dV.

Comprova-se facilmente que W₂ > W₁. Alguma coisa está errada neste raciocínio. Ou não?

Será que a solução de um problema tão simples como este foge ao domínio da termodinâmica clássica?

Observação: A termodinâmica clássica estuda estados iniciais e finais; e em seus cálculos não devem ser levados em consideração efeitos tais como o atrito entre a membrana móvel e o recipiente.

Conforme referi na mensagem 13: "Descobri esse paradoxo em 1975 e o apresentei em seminário da disciplina de Termodinâmica Aplicada a Sistemas Biológicos, na Usp (Fisiologia). Até hoje não encontrei uma solução convincente, por mais que tenha procurado. Postei o mesmo em vários newsgroups nacionais e internacionais e o paradoxo persiste, sem solução."

Entre a mensagem 13 e esta fui obrigado a refletir muito sobre os fundamentos da termodinâmica e, ao que tudo indica, consegui, dentre muitas idéias que foram aparecendo e que fui passando para o papel, encontrar a solução para o paradoxo. Uma única frase do que escrevi nestas mensagens gerou-me o insight. Espero brevemente apresentar a possível solução, acrescentando, talvez, algumas idéias novas relativas à irreversibilidade e que nunca me ocorreram antes. Foi pensando nisso que escrevi acima, no terceiro parágrafo desta mensagem: "Nem sempre o paradoxo, ao ser resolvido, mostra-se inconsistente. Não raramente, chama a atenção para algo inerente à teoria e que não estava sendo devidamente valorizado, a ponto de ter gerado o paradoxo."

 
Ü    Índice do Diálogo
Próximas Mensagens    Þ

DHTML Menu By Milonic JavaScript