Estudo do Movimento
Estudo do Movimento
através da Metodologia Net-In
Alberto Mesquita Filho
Página 4
Capítulo 2 - 1ª Parte
Capítulo 2: Refinando as medidas
Apesar dos progressos efetuados no capítulo 1 e na resolução dos exercícios desse capítulo, ainda estão faltando algumas ferramentas indispensáveis para que possamos estudar os movimentos virtuais (movimentos simulados na tela do computador) em sua completude. Uma das finalidades deste capítulo será a de caminhar neste sentido. Para tanto você terá que importar alguns pequenos softwares e eu vou sugerir que você opte por aqueles que mais irão se afinar com o nosso estudo. Alguns são gratuitos (freeware) ou, pelo menos, estavam sendo oferecidos gratuitamente enquanto eu estava escrevendo este trabalho. Outros poderão ser utilizados gratuitamente um certo número de vezes e/ou durante um certo tempo (shareware), após o que o software deixará de funcionar, a menos que você o registre, e este registro poderá implicar no pagamento de uma determinada taxa. De qualquer forma eu acho que valerá a pena testar pelo menos dois softwares, mesmo porque o número de vezes e/ou este intervalo de tempo é bastante razoável. Enquanto durar a funcionalidade desses dois softwares poderemos evoluir bastante ou, até mesmo, concluir este artigo (3 capítulos). Após esse tempo, e se necessário for, deixarei a seu critério a opção de registro, com pagamento, ou a procura por um outro software equivalente e, quiçá, freeware. Digo apenas que não tenho nenhum interesse nem participação na venda desses softwares, que acabei encontrando em minhas andanças pela Internet (e paguei por eles
).
Vamos começar pelo mais simples: a régua de tela. Existem muitas réguas de tela disponíveis, tanto como freeware quanto como shareware. Você poderá encontrá-las numa simples pesquisa Google utilizando as expressões "régua", "régua de tela", "ruler", "screen ruler", "virtual ruler" etc, ou então em sites de download. Uma das melhores é a JRuler Pro 3.1 (shareware - 15 days trial), cujo download poderá ser feito clicando aqui → [Site 1 ou Site 2]. Em fevereiro de 2010 o preço era de $19 (dezenove dólares). Faça pelo menos o download e utilize a régua durante o período de teste (15 dias). No item que se segue admitirei que você fez o download, instalou a régua e está na fase de testes.
2.1 Utilizando a régua de tela
A primeira coisa que você deverá notar ao utilizar uma régua de tela é que a medida em centímetros pode não corresponder à realidade. Mas isso não deve preocupá-lo pois, sempre que for necessário, poderemos encontrar uma forma de corrigir a medida. O fator de correção será diferente de computador para computador (está relacionado ao tamanho da diagonal do monitor e à resolução da tela). Para que você tenha uma idéia, quando leio 10cm na tela do meu computador com a régua JRuler Pro (versão anterior, ou 3.0), esses 10cm correspondem a quase 14 cm, quando confrontados com a medida feita com uma régua normal (régua escolar).
Para sanar essas discrepâncias e evitar confusões, vamos trabalhar apenas com a escala em pixels da régua, pois embora o tamanho do pixel seja diferente de um computador para outro, o número de pixels entre dois pontos de uma figura transferida de um computador para o outro é o mesmo. Após instalar a régua, verifique se ela está configurada para pixels. Se não, clique no meio da régua, onde se lê o padrão de medida que está sendo utilizado e modifique para "pixels". Rigorosamente falando o pixel não é uma medida de distância [1], mas do ponto de vista prático ele pode ser utilizado como tal.
Vamos agora verificar o quão mais fácil ficará a nossa tarefa de medir distâncias. Em primeiro lugar tente medir a distância entre os marcos vermelho e verde do gif animado 02 visto no capítulo 1 e depois prossiga com a leitura.
gif animado 02:
si sfA rigor você nem precisará ler da maneira convencional que aprendeu a fazer com uma régua comum. Coloque a régua em cima do gif animado e a seguir torne-a tão transparente quanto necessário for para que você possa enxergar os marcos vermelho e verde com nitidez (faça isso clicando em cima da régua com o botão direito do mouse e a seguir, e com o botão esquerdo, em "More transparent (-)" tantas vezes quantas julgar necessário). Dê agora um duplo clique bem em cima do marco vermelho e logo a seguir outro duplo clique bem em cima do marco verde. O resultado (distância entre os marcos em pixel) aparecerá quando você passar com o mouse em cima da linha que une esses dois pontos (L = ...). Compare este valor com aquele determinado no capítulo 1 (final do item 1.4, expressão 1.1). Não deixe de fazer uma estimativa para a incerteza da medida [Se necessário, vide Ajuda 3.2].
Importante: Como os marcos vermelho e verde não são puntiformes e são iguais em formato (são quadrados de lado igual a 10pix), procure escolher pontos equivalentes em ambos e fáceis de serem localizados: ou na extrema esquerda, ou bem no centro, ou na extrema direita. Esta regra valerá também para quando formos estudar o movimento de objetos virtuais rígidos e não puntiformes.Veja agora como é bem mais fácil calcular a distância entre os marcos 1 e 2, apresentados na figura 1 da página de exercícios do capítulo 1. Antes você precisará colocar a régua em cima da figura e redimensioná-la, o que pode ser feito arrastando convenientemente as bordas da régua.
Depois disso proceda de maneira semelhante àquela efetuada na medição anterior e leia o resultado na própria régua. Compare com o valor obtido quando resolveu o exercício 1 do capítulo 1.
2.2 Multiplicador da Área de Transferência
Como já foi comentado no capítulo 1, item 1.4, "para o estudo do movimento de um objeto torna-se necessário o conhecimento de pelo menos duas variáveis (o lugar ocupado pelo objeto e o instante em que ocorre essa ocupação), em pelo menos duas condições". Na maioria dos casos o número de condições deve ser maior. Até o momento não conseguimos sequer satisfazer essas duas condições necessárias e, em virtude disso, ainda não foi possível efetuar o estudo completo de nenhum dos movimentos apresentados. Quando muito o que fizemos foi determinar a distância que um objeto "deveria percorrer" e, logo a seguir, verificamos quanto tempo ele demorou para percorrer essa distância. Ou seja, nosso estudo está limitado à constatação de poucas características relacionadas aos movimentos e ao fato de algumas das propriedades desses movimentos já serem conhecidas de antemão (no caso, por onde os objetos virtuais deverão passar → os famosos marcos até agora utilizados). Mas como poderemos efetuar esse estudo se não tivermos este conhecimento prévio? Isso é o que acontece na realidade e no nosso dia-a-dia, e é isso o que o estudo virtual pretende simular.
Para sanar esta dificuldade devemos implementar a maneira como o computador registra as imagens que se passam na tela. Ou seja, o computador deve estar adaptado com alguma ferramenta capaz de armazenar inúmeras imagens da tela e que se sucedem em intervalos bem pequenos de tempo, da ordem de frações de segundo. Estas ferramentas existem e recebem a denominação de multiplicadores da área de transferência. Para isso você encontrará, na Internet, tanto sharewares quanto freewares.
Nos itens que se seguem apresentarei o funcionamento do Clipboard Box V3.6 que é aquele que possuo no meu computador. Trata-se de um shareware [A versão atual é V4.2 - $19,99 em fev/2010] que consegue armazenar até 100 imagens ao mesmo tempo. Se você não ficar abrindo e fechando (Quit) o software e/ou ligando e desligando o computador com frequência, o período de teste poderá durar bastante, o suficiente para você verificar se deve ou não comprar o software. Outro multiplicador (freeware) está indicado abaixo, em Notas e Referências [2], e se presta também ao nosso estudo, ainda que funcionando de maneira ligeiramente diferente.
Em termos de ferramentas de medida, e supondo que você esteja pensando seriamente em instalar, no seu computador, um multiplicador da área de transferência, estaremos, a partir de então, razoavelmente bem aparelhados, apesar de ainda estar faltando um cronômetro um pouco mais sofisticado do que aquele apresentado na página de exercícios do capítulo 1 (o cronômetro net-in).
2.3 Algumas considerações a respeito de referenciais
Referencial, como é estudado em mecânica, implica na idéia da existência de uma estrutura associada a um observador, seja este real ou hipotético. A tela de um computador pode, sob certos aspectos, encaixar-se na categoria de referencial. A ressalva, implícita na expressão "sob certos aspectos", é feita principalmente pelo fato de estarmos simulando uma realidade às custas do estudo de movimentos virtuais; ou seja, movimentos relacionados a objetos que na realidade não são reais ou materiais e sim imagens que sequer possuem massa, uma das características marcantes e fundamentais da matéria.
Com grande frequência diz-se que "um referencial pode ser descrito abstratamente por um sistema de coordenadas espaciais e temporais" [3]. Esta é uma verdade que deve ser interpretada com muito cuidado, para que não fique a impressão de que referencial e sistema de coordenadas sejam uma coisa só. Um sistema de coordenadas pode ser admitido como algo a representar um referencial, mas é importante perceber que o referencial já existia antes da escolha deste seu representante. Por outro lado, um mesmo referencial pode comportar vários sistemas de coordenadas, cada um destes tendo, como características: (1) uma posição bem definida (comumente chamada origem do sistema) e (2) eixos (ou algo equivalente) acoplados a (3) unidades de medida convenientes para o estudo em consideração, dentre outras. Particularidades importantes e relacionadas aos referenciais são melhor apreciadas quando se estuda a relatividade do movimento. Por ora é importante que fique bem claro que se um sistema de coordenadas está em movimento em relação a outro, os dois sistemas estão situados em referenciais distintos, podendo-se dizer, com o intuito de economizar palavras, que são referenciais distintos, ou então, e de maneira mais apropriada, que representam referenciais distintos.
O observador, via de regra, fixa-se num referencial que seria aquela estrutura que, como dissemos no início do item, está associada a ele (observador). Uma vez feita esta opção, ou uma vez definido o que viria a ser esta estrutura a que se ater, o observador não tem outra escolha que não seja a de caracterizar o tipo de sistema de coordenadas que irá representar este referencial onde ele se situa física ou mentalmente. E para isso o seu grau de liberdade é bastante grande.
Assim, quando eu digo que o referencial do meu estudo é a tela do computador, o referencial já está bem definido, não havendo a necessidade de me reportar àqueles quadradinhos vistos nos exercícios anteriores e chamados por marcos. Posso até utilizá-los, ciente da existência de outras escolhas ou manobras que podem se mostrar mais convenientes. Aqueles marcos poderiam até mesmo nem existir, não fosse pelo fato de que, na ocasião em que fomos obrigados a utilizá-los, estávamos mal equipados ou com poucas ferramentas de estudo, o que não deve estar acontecendo agora. Vamos então rever o movimento do gif animado 2 sem os quadradinhos vermelho e verde, para que essa idéia fique nítida, assim como para que possamos avaliar algumas dentre as inúmeras vantagens de se ter um multiplicador da área de transferência.
2.4 Como medir e registrar as medidas
Observe as características gerais do movimento representado no gif animado abaixo.
gif animado 03:
Algo que chama a atenção, e que já comentei de passagem no capítulo 1, é o fato do movimento ocorrer aos saltos, como se o espaço estivesse quantizado. Esta sensação será maior ou menor conforme a qualidade do gif produzido ou do software que o reproduz, mas sempre estará presente. Para que você tenha uma idéia, veja por exemplo como fica o mesmo conjunto de imagens quando visualizado também em página web (no mesmo navegador), mas transformado em arquivo avi: clique aqui para observar e comparar [arquivo de 6MB e portanto demora para entrar - caso queira assisti-lo continue a leitura enquanto espera pelo download]. Quase que chega a ficar a sensação ilusória de que o movimento observado é espacialmente contínuo, como acontece na realidade com os objetos materiais do nosso dia-a-dia.
Por ora vamos nos concentrar no gif animado deixando esta característica de lado. Vamos assumir a continuidade espacial como algo que realmente deveria estar acontecendo em nossa simulação. Pergunto então: O que mais chama a atenção quando observamos o movimento representado no gif animado 03?
Eu diria que uma das características é o fato do movimento se dar em linha reta e outra, não menos importante, é que nos fica a sensação de uma certa uniformidade, como se pudéssemos dizer, se bem que de maneira aproximada, que o objeto virtual percorre espaços iguais em tempos iguais. Isto caracterizaria o que é chamado movimento uniforme e, no caso considerado, retilíneo. Verificar se o objeto está ou não dotado desta característica será um dos objetivos do desafio ora proposto, qual seja: Como verificar se há ou não este tipo de uniformidade no movimento em consideração? Pense no que você poderia fazer para vencer mais este desafio e, a seguir, prossiga com a leitura.
A esta altura você já deve ter instalado, no seu computador, um dos multiplicadores da área de transferência dentre aqueles sugeridos. Neste caso, é provável que você já tenha "fuçado" o suficiente a ponto de já estar a par das manobras mais gerais (como abrir, como registrar uma imagem etc). Se ainda não o fez, está na hora de fazer, agora com uma finalidade em mente: a de resolver o desafio proposto. Abra então a janela do software.
Minimize a janela do Clipboard Box para que ele fique fora da tela [4], mas não o feche [Tanto o botão de minimizar quanto o de fechar estão no canto superior direito]. Coloque o gif animado 03 (reproduzido abaixo) numa posição conveniente da tela (ou seja, numa altura média) e a seguir abra o cronômetro net-in clicando aqui. Ajuste a posição da janela do cronômetro para que fique mais ou menos centralizada e um pouco acima ou um pouco abaixo do gif animado. Se quiser zerar o cronômetro é só pressionar a tecla F5 com a janela do mesmo focalizada. Isso não é necessário mas será conveniente (irá facilitar os cálculos), principalmente se o cronômetro estiver próximo de ultrapassar a marca de 1min = 60s ou qualquer outro valor inteiro de minutos. A seguir coloque um dos dedos acima da tecla PrintScr (sem pressioná-la) e, assim que a bolinha aparecer do lado esquerdo do gif, comece a pressionar a tecla repetidamente e rapidamente, até que a bolinha desapareça do lado direito. Se você for rápido conseguirá obter um pouco mais do que 20 imagens. Pronto! Pode fechar o cronômetro. A primeira parte da experiência acabou. Agora cabe-nos a tarefa de fazer a leitura, registrar os dados e analisar os resultados.
gif animado 03:
Maximize novamente o Clipboard Box (dando um duplo clique no seu ícone, que deve estar na barra de tarefas, à direita). Através da barra de rolamento do Clipboard Box verifique quais são os clipes pertencentes à experiência e apague os demais (a menos que você tenha interesse em conservar um ou mais desses clipes). Para isso, vá selecionando um a um os clips indesejados e vá clicando no botão "Clear Selected". Depois disso clique em Save All e, logo a seguir, em OK. Os clipes serão salvos em arquivos "bmp" que permanecerão provisoriamente numa pasta do diretório do software denominada "saved" (provavelmente em C:\Arquivos de programas\Clipboard Box\saved). Você não precisará memorizar este endereço, pois a pasta se abrirá clicando-se em View Saved (na janela do Clipboard Box).
Importante: A próxima vez que você utilizar o recurso "Save All" as imagens contidas nesta pasta serão excluídas e substituídas por novas imagens, logo tome cuidado com este botão. Não utilize mais este botão até terminar a próxima etapa da experiência, ou seja, até registrar os valores medidos numa planilha do Excel. Em dúvida salve as imagens em uma pasta provisória, a fim de que você possa eliminá-las com segurança num futuro próximo (a menos que contenham dados de uma experiência real e você pretenda conservá-las como testemunho experimental). O ideal, no nosso caso, seria registrar logo os resultados (o que será feito a seguir) e deixar que as imagens sejam eliminadas naturalmente.Na janela do Clipboard Box clique em "View Saved" e a seguir feche o software pois ele não será mais utilizado por ora. Na janela que se abre (pasta "saved") dê um duplo clique no arquivo da primeira imagem da nossa série, e que deve ser img1.bmp. A imagem surgirá provavelmente no "Visualizador de imagens e fax do Windows". Se isto não acontecer volte à pasta "saved", clique com o botão direito do mouse no arquivo correspondente (img1.bmp) e depois, com o botão esquerdo, em "abrir com Þ Visualizador de imagens e fax do Windows". Feito isso pode fechar a janela da pasta "saved".
Abra o Excel e disponha as janelas do Visualizador e do Excel da maneira mostrada clicando-se aqui. Você já fez algo semelhante no capítulo 1 (vide figura 7). Acesse agora a régua de tela e disponha-a em uma posição conveniente para a medida da posição da bolinha (por exemplo, como mostrado na figura 11 abaixo). Ajuste a transparência da régua para que a bolinha fique bem visível; e também o tamanho da régua (ajuste pelas margens) de maneira a cobrir todo o trajeto que virá a ser percorrido pela bolinha e evitando que a régua cubra a leitura do cronômetro. Feito isso não se deve mais mover nem a régua e nem a janela do Visualizador, até que se leia os valores fornecidos por todas as imagens.
Perceba que o sistema coordenado que acabamos de escolher para representar o nosso referencial é a régua e os zeros dos eixos cartesianos x e y devem permanecer fixos neste referencial, que nada mais é senão a tela do computador. Você não precisa se preocupar em saber onde exatamente estão os eixos [ou então onde (x,y) = (0,0)], ainda que isso seja possível; mas deve se preocupar com o cuidado a ser tomado para que esses eixos permaneçam sempre no mesmo lugar.
Fixadas as duas janelas (Visualizador e régua), o passo seguinte é efetuar as leituras e digitá-las nas células do Excel. Coloque o apontador do mouse no centro da bolinha, como mostra a figura 11 e leia o valor de x que aparece na régua, à esquerda, logo após uma flecha apontando para a direita. No caso exemplificado na figura, x(1) é igual a 161pix e t(1) = 4,8s [seus valores certamente serão outros]. Como os valores que você leu referem-se à primeira figura (img1.bmp), registre-os nas células A1 e B1 da planilha do Excel: [x(1) em A1 e t(1) em B1].
Figura 11: Explicação no textoA seguir clique no botão "Próxima imagem" (
) da janela do Visualizador e surgirá na tela a figura img2.bmp. Registre o valores de x(2) e t(2) respectivamente nas células A2 e B2 do Excel. Repita este procedimento até chegar na última figura (imgn.bmp, sendo n o número de imagens que você obteve ) e que deverá ter os valores x(n) e t(n) registrados nas células An e Bn. Com isto você não só terá concluído a etapa de leitura das medidas, como também terá registrado todos os seus valores. Resta agora proceder à análise dos resultados e isto deve ser feito no Excel, logo as outras janelas (régua e visualizador) já podem ser fechadas.
Salve o arquivo Excel num local adequado e com um nome conveniente (por ex., cap2.xlsx), afim de que você possa se lembrar do mesmo quando for ler o item 2.6. Vamos agora para um intervalo matemático, não sem antes fazer uma ressalva:
Cuidado ao interpretar os valores obtidos como sendo a distância percorrida s em pix. Se assumirmos os x's obtidos como sendo iguais aos espaços percorridos (s) em pix estaremos cometendo um tipo de erro que será descrito no item 8 como erro sistemático. Você conseguiria localizar este suposto erro? E porquê estou chamando de "suposto" erro? Afinal, é ou não é um erro? Isto será esclarecido no item 2.8. Até lá vamos assumir por simplicidade que x = s cientes de que, até prova em contrário, podemos estar cometendo um erro.
2.5 Intervalo Matemático: Domínio e Função de uma variável
2.5.1 Domínio de uma variável é o conjunto de valores que ela pode tomar. Exemplo: Seja s o conjunto dos pontos (x,y,z) ocupados pelo centro geométrico de um corpo rígido que se move retilineamente, ocupando sempre o eixo dos x. Neste caso s pode ser escrito como s = (x,y,z) = (x,0,0) ou, de maneira simplificada, s = x. Nesta maneira simplificada está implícito o fato de estarmos considerando o movimento do corpo rígido como ocorrendo em uma dimensão. O domínio de s, assim definido, pode ser imaginado como sendo o contínuo igual ao conjunto do produto dos números naturais pela unidade elementar de comprimento.
No caso ora em consideração (gif animado 03) estamos lidando com um objeto virtual e, como já assinalado, o correspondente domínio de s não será mais um contínuo e sim um conjunto de valores discretos que correspondem a posições definidas por quem construiu o gif animado. Não obstante, optamos por assumir uma idealização, qual seja, aceitar a continuidade espacial como algo que realmente deveria estar acontecendo em nossa simulação. Frente a essa idealização, podemos pensar neste domínio de s como algo a identificar-se com o domínio considerado no parágrafo anterior.
A tabela 2.1 (ao lado) apresenta um conjunto de valores experimentais (obtidos da maneira descrita no item 2.4), tanto para a variável s = x (posição de um objeto virtual), quanto para a variável t (instante em que o correspondente s foi observado). A primeira coluna representa então o que poderíamos chamar de um domínio experimental de s, ou seja, o conjunto dos valores observados de s. Este domínio experimental de s está contido no domínio de s mais geral e definido anteriormente, mas é importante observar que estamos falando de domínios distintos, ainda que relacionados.
A segunda coluna, por sua vez, representa o que poderíamos chamar domínio experimental de t. De maneira análoga ao que foi dito nos parágrafos precedentes para s, poderíamos dizer que o domínio experimental de t (conjunto dos valores obtidos em uma experiência) está contido no domínio de t que pode ser imaginado como sendo o contínuo igual ao conjunto do produto dos números naturais pela unidade elementar de tempo.
2.5.2 Função de uma variável: Diz-se que uma variável s é função de uma variável t se a cada valor do domínio de t corresponder um e apenas um valor do domínio de s. Neste caso escrevemos s = f(t) para simbolizar e/ou explicitar a dependência entre os valores de t e os valores de s. Alternativamente poderíamos ter escrito s = g(t), ou s = F(t), ou s = G(t) ou, até mesmo, s = s(t) etc.
A tabela 2.1 apresenta todos os valores assumidos pela função se = f(te), onde o índice "e" foi aqui acrescentado apenas para que fique claro que estamos trabalhando com domínios experimentais de s e de t. Via de regra não tomaremos este cuidado e expressaremos este tipo de função experimental como s = f(t), mesmo porque trabalhamos com a esperança de que os dados observados sejam representativos de uma função mais geral e a retratar valores de t e de s não contidos na tabela, mas pertencentes a domínios mais amplos e geralmente contínuos, como aqueles definidos acima.
2.6 Como organizar os dados experimentais?
A planilha 1 (Plan1) do arquivo Excel, salvo no final da leitura do item 2.4, contém uma função experimental do tipo s = f(t) expressa na matriz A1:Bn. Para a planilha tornar-se informativa e útil em observações futuras, convém fazer algumas modificações. Do contrário, e dentro de poucos dias, nem mesmo você conseguirá decifrar o significado do conjunto de dados aí apresentados.
O importante é dispor os dados de maneira harmoniosa e, acima de tudo, de fácil leitura e manuseio. Existem várias maneiras para se atingir este objetivo e você deverá ir testando para verificar qual é aquela que mais o satisfaz. Vou efetuar algumas considerações, em especial no que diz respeito à disposição dos elementos da planilha, a fim de facilitar o manuseio dos dados. Você, por outro lado, deve se sentir a vontade para adaptar essa disposição ao seu estilo, sem promover uma redução da funcionalidade. Abaixo você encontrará um roteiro escrito com a finalidade ajudá-lo nesta tarefa, portanto sugiro que leia este item até o fim antes de realizar as modificações.
Em primeiro lugar, estão faltando alguns títulos na planilha e a relacionarem-se com as seguintes perguntas: Título 1: A que se refere o estudo? Título 2: O que representa a tabela, ou a matriz com o conjunto de todas as medidas? Título 3: O que representam as colunas desta tabela? Consequentemente, teremos que modificar o posicionamento da matriz para dar lugar a esses títulos, deslocando portanto os valores registrados. A posição atual pode ser considerada a ideal apenas para a coleta de dados.
A maneira como iremos trabalhar com os dados é outro fator limitante; e já que vamos modificar a localização da matriz de dados, convém já irmos pensando em qual deveria ser a sua apresentação final. A bem da clareza, devemos introduzir uma coluna para os valores de n (n = 1, 2, 3...), como mostrado na tabela 2.1 acima. Observe, nesta tabela, a largura das colunas e se devemos ou não centralizar alguns de seus elementos. Verifique quais caracteres, na sua opinião, deveriam ser expressos em negrito e quais poderiam continuar no estilo normal; ou então o tipo de fonte a ser utilizado. É bom já ir aprendendo como satisfazer, rapidamente, esses caprichos.
Outro fator que não pode ser desprezado, refere-se ao significado da matriz e que, como vimos, representa uma função do tipo y = f(x), qual seja: s = f(t). Ora, uma função do tipo s = f(t) pode ser representada graficamente num sistema de dois eixos cartesianos ortogonais (figura 12). No eixo das abscissas (horizontal) costuma-se colocar os valores do que estamos considerando como variável independente, ou o argumento da função, e que, para o caso considerado, seria o tempo t. No eixo das ordenadas costuma-se colocar os valores da variável dependente, ou seja, a imagem s de t ou a função propriamente dita. Esses valores, projetados dois a dois (t com o seu correspondente s) para a área destinada à representação da função, fornecem, no seu conjunto, a representação pictórica da função, ou seja, o gráfico da função.
Figura 12: Eixos cartesianos ortogonaisEste gráfico pode ser construído rapidamente no Excel, mas para usufruirmos dessa rapidez devemos dispor os elementos da matriz de uma forma conveniente. A coluna da variável independente (X para o Excel, e t para o nosso exemplo) deve estar disposta à esquerda da variável dependente (Y para o Excel, e s para nosso exemplo). Ou seja, de maneira exatamente contrária àquela em que você foi orientado a representar os dados experimentais na planilha 1. Convém então inverter a disposição dessas colunas, o que pode ser feito rapidamente.
Há que se pensar também na possibilidade de imprimir alguns ou todos os tópicos contidos na planilha do Excel. Para que a impressão não saia truncada convém distribuir os elementos dentro de limites bem definidos, fáceis de serem localizados e a caracterizarem o que poderíamos chamar "páginas do Excel".
Enfim, aí estão relatadas as mudanças que você já deve ir efetuando em sua planilha. Para tornar a tarefa mais fácil siga o roteiro de ajuda que aparecerá clicando-se aqui.
2.7 Gráfico da função experimental expressa na Tabela 2.1
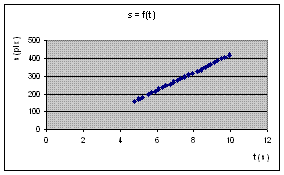
Caso você tenha efetuado as modificações sugeridas, a planilha 1 do Excel já está pronta para receber o gráfico da função s = f(t). A tarefa é bastante simples. Em caso de dúvida clique em um dos seguintes links: Þ Excel do Office 2007 ou de Versões Anteriores. Seguindo as instruções você irá obter algo semelhante ao que é mostrado na figura 13 abaixo, construída no Excel com os valores de t e s plotados na Tabela 2.1 acima. Podemos agora responder ao desafio proposto no item 2.4, qual seja: Como verificar se o objeto em consideração está ou não em movimento uniforme?
Figura 13: Gráfico da função s = f(t)
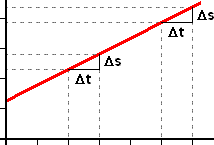
expressa na Tabela 2.1.Chama a atenção, neste gráfico, a linearidade quase perfeita dos pontos representativos da função. Isto demonstra que o objeto em consideração percorre distâncias iguais em tempos iguais, conforme queríamos demonstrar (item 2.4) [a menos de uma discretíssima incerteza que não foi levada em consideração e que será comentada em outros exercícios] [5]. A figura 14 esclarece melhor um dos critérios pelos quais pode-se chegar a essa conclusão: através da semelhança de triângulos demonstra-se facilmente que se os Δt´s considerados na figura tiverem comprimentos iguais, os correspondentes Δs´s também serão iguais.
Figura 14: Explicação no texto.* * * * *
◄▬ Para voltar ou avançar clique nas figuras ▬►
- Caso você tenha interesse em conhecer mais sobre o pixel, vide A Brief History of "Pixel" ou então Pixel, from Wikipedia.
- Outro multiplicador da área de transferência (freeware): M8 Free Multi Clipboard: Muito bom, funciona em todas as versões do Windows e suporta até 25 cópias [versão "simple" (o que é mais do que suficiente para o nosso estudo)]. Para fazer o download do freeware clique aqui ou dirija-se ao link acima. Existem também sharewares [$9.99 (versão "simple") e $19.99 (versão "spartan")] e para obter estas versões você deverá ir à Home Page do site.
- Esta expressão é encontrada no Dicionário Eletrônico Houaiss, sob a rubrica Física.
- Como medida alternativa você pode clicar em Options, depois em Position e, por fim, desmarcar a opção "Always on the top of all windows".
- É sempre importante evidenciar o valor da incerteza, por mais discreta que ela possa vir a ser. Neste caso ela está sendo deixada de lado por motivos de ordem didática.