Estudo do Movimento
Estudo do Movimento
através da Metodologia Net-In [1]
Alberto Mesquita Filho
Página 1
Capítulo 1 - 1ª ParteCapítulo 1 - Medidas de Espaço e Tempo no Computador
- Considerações Preliminares
- Criando Atalho para a Área de Transferência (clipboard)
- Visualizando e Utilizando a Área de Transferência
- Testando os seus reflexos
- Espaço Percorrido
- Intervalo de tempo
- Uma breve introdução à teoria dos erros
- Erros e Desvios
- Exercícios
Capítulo 2 - Refinando as medidas
- Utilizando a régua de tela
- Multiplicador da Área de Transferência
- Algumas considerações a respeito de referenciais
- Como medir e registrar as medidas
- Intervalo Matemático: Domínio e Função de uma variável
- Como organizar os dados experimentais?
- Gráfico da função experimental expressa na Tabela 2.1
- Tipos de erros experimentais
- Cronômetro de tela
- Exercícios
Capítulo 3 - Movimentos Uni, Bi e Tridimensionais
- Dimensões e realidade
- Dimensões e movimento
- Dimensões e Trajetória
- Dimensões e sistemas de coordenadas espaciais
- Exemplificando a abordagem bidimensional. Mais um desafio
- Análise gráfica
- Significado das funções x e y
- Mais sobre erros e desvios
- Exercícios
Capítulo 1: Medidas de Espaço e Tempo no Computador
1.1 Considerações Preliminares
No decorrer desta jornada, você será desafiado a resolver inúmeros problemas relativos ao estudo do movimento (mecânica) e que irão aparecendo em ordem sequencial de dificuldade. Você poderá tentar resolvê-los sozinho e a sua maneira (recomendado) e a seguir verificar como o problema poderia ter sido resolvido a minha maneira.
Uma das características mais interessantes e importantes relacionada ao movimento é a relatividade e, a esse respeito, um de seus aspectos peculiares poderia ser sintetizado, de maneira bem elementar, nas seguintes palavras: Quando dizemos que algo está em movimento, na realidade estamos pretendendo dizer que algo está se movendo em relação a alguma outra coisa que estamos assumindo estar em repouso [2]. O gif animado 01, mostrado abaixo, representa a figura de um automóvel movendo-se na tela de seu computador. Inúmeros pontos da tela de seu computador estão subliminarmente sendo considerados por você como em repouso, enquanto a figura que representa o automóvel é assumida como estando em movimento em relação a esses pontos.
[Nos parágrafos que se seguem, sempre que precisar me referir a "figura que representa o automóvel", é possível que eu chegue a citar simplesmente "automóvel". Coisas do mesmo gênero e em contextos semelhantes irão acontecer em outras seções deste mesmo artigo.]
gif animado 01:
No gif-animado vê-se um objeto em repouso (haste vertical) representando alguma coisa que está se sobrepondo à trajetória do automóvel (rua ou estrada) e que poderia ser um poste no acostamento ou uma árvore, enfim um objeto que pode ou não vir a ser valorizado em nosso estudo.
O primeiro desafio que lançarei é o seguinte: Você seria capaz de "fotografar" o gif animado num momento em que o automóvel está passando pela haste vertical? Pense bem antes de prosseguir com a leitura.
Uma resposta imediata seria: Sim, com uma máquina fotográfica. Ou então, mais fácil ainda, com aquele celular sofisticado que tira fotografias e que pode ser que esteja ao seu lado. Mas não é esta a resposta que estou esperando que você dê. Você deve notar que escrevi fotografar entre aspas. Sim, eu estou sugerindo que você reproduza, na tela do seu computador, uma imagem momentânea (aquela de quando o automóvel passa pela haste vertical) utilizando os recursos que o seu computador possui.
Perfeito! Você agora deve estar pensando na "Área de Transferência" do seu computador, aquela que você utiliza frequentemente através do recurso Copiar/Colar, mas... Como obter uma imagem instantânea da tela do seu computador? Caso você não saiba, os dois itens a seguir irão ajudá-lo nessa tarefa.
1.2 Criando Atalho para a Área de Transferência (clipboard)
No artigo Dicas para Windows XP - Parte 2 [do site InfoWester] lê-se o seguinte: O Visualizador da Área de Transferência não existe mais no menu Iniciar do Windows XP, mas ele ainda está disponível no sistema (com o nome de Visualizador da Área de Armazenamento). Para usá-lo, vá em C:\Windows\System32 e crie um atalho para o programa clipbrd.exe na Área de Trabalho do Windows.
Infelizmente as novas versões do Windows (Vista ou 7.0) não oferecem mais esta opção. Nada que não possa ser contornado. Uma das maneiras seria copiar o arquivo clipbrd.exe de um computador onde esteja instalada a versão XP. Outra, como veremos logo abaixo, será utilizar o Paint (ou MSPaint).
Se você estiver usando o Windows XP, localize o arquivo clipbrd.exe na pasta C:/WINDOWS/system32 (Ü clicando aqui é bem possível que a pasta se abra no seu computador). Se estiver usando o Windows Vista ou 7.0 e optou por copiar o arquivo, localize o diretório onde o mesmo foi copiado.
Em qualquer dos dois casos, crie um atalho através do seguinte procedimento: clique com o botão direito do mouse no arquivo clipbrd.exe e, logo a seguir, em Copiar. Feche a janela do Windows Explorer e vá para a área de trabalho do Windows (Desktop). Clique com o botão direito num ponto livre desta tela e, logo a seguir, e com o botão esquerdo, em Colar Atalho.
Como iremos utilizar bastante este recurso, talvez seja interessante levar esse atalho para a barra de tarefas. Isso poderá ser feito arrastando o ícone do atalho para a porção esquerda da barra de tarefas, próximo ao botão iniciar. A barra de tarefas deverá ficar semelhante àquela mostrada na figura abaixo. A seguir você poderá excluir o ícone que permaneceu na área de trabalho.
Figura 1: Atalho para a área de transferência.Se você optar pela utilização do Paint [Windows Vista], poderá criar um atalho para o mspaint.exe da seguinte forma: Clique em Iniciar na Barra de Tarefas e digite mspaint. O arquivo mspaint.exe aparecerá logo acima, no menu Iniciar. Clique aí com o botão direito do mouse e proceda de maneira idêntica àquela indicada dois parágrafos acima para o clipbrd.exe.
1.3 Visualizando e Utilizando a Área de Transferência
Um simples clique no atalho para clipbrd criado na seção anterior irá abrir uma janela revelando o conteúdo armazenado temporariamente na área de transferência. No caso do Paint o processo é um pouquinho mais trabalhoso: clique no atalho mspaint para abrir o Paint e no menu Editar do Paint clique em Colar.
A pergunta que surge a seguir é a seguinte: Como levar a imagem que está neste momento na tela do seu computador para a área de transferência? Caso você não saiba, o processo é muito simples. Procure no teclado de seu computador por uma das teclas onde se lê PrtScr (Print Screen). Cada vez que você teclar PrtScr, a imagem que está na tela de seu computador será armazenada temporariamente na área de transferência. Faça isso agora e observe o resultado clicando no atalho que você acabou de colocar na barra de tarefas (Atalho para clipbrd ou para mspaint).
Ás vezes é conveniente reproduzir apenas uma janela que não esteja ocupando toda a tela do computador. Neste caso você deverá manter a tecla Alt pressionada por um certo intervalo de tempo e, durante esse intervalo, pressionar rapidamente a tecla PrtScr. Com isto, a janela que detém o foco, no momento em que você utilizar o comando Alt + PrtScr, será copiada para a área de transferência [3].
Podemos agora retornar ao problema original, qual seja, o desafio lançado no item 1.1: "Você seria capaz de "fotografar" o gif animado num momento em que o automóvel está passando pela haste vertical?" Para facilitar a tarefa o gif animado 01 está reproduzido abaixo.
gif animado 01:
Procure manter a figura a ser "fotografada" no alto da tela. Quando o automóvel estiver passando pela haste vertical, pressione a tecla PrtScr e a seguir veja o resultado abrindo o visualizador da área de transferência (ou seja, clicando no atalho para clipbrd.exe).
Vamos refinar um pouco mais o desafio. Seria possível obter a "fotografia" no momento exato em que a imagem do carro "encosta" na imagem da haste vertical? A figura 2 representa como seria esta situação.
Figura 2: Explicação no texto.A tarefa não é das mais difíceis e a meta poderá ser atingida com pouquíssimas tentativas. Se formos fotografar de fato um automóvel que passa pela rua a tarefa será bem mais difícil e o número de tentativas certamente será muito maior. É importante saber o porquê dessa facilidade atual, mesmo porque na maioria das vezes iremos trabalhar com movimentos simulados que estarão acontecendo na tela de seu computador e produzidos através de gifs animados como aquele mostrado acima.
Os gifs animados são construídos com figuras que se superpõem de maneira não contínua, mas discreta. Em outras palavras, isso significa dizer que entre uma figura e a seguinte existe um espaço que não chega a ser, em nenhum momento, ocupado pela imagem do objeto que está sendo representado. Neste caso a idéia de um movimento contínuo é ilusória e tanto mais quanto maior for esse espaço entre duas imagens sequenciais. Se observarmos com atenção o gif animado 01 (acima), perceberemos que o automóvel move-se aos saltos. A figura 3 mostra algumas imagens, dentre aquelas existentes no gif animado 01, a representarem situações em que o automóvel está próximo da haste vertical.
Figura 3: Explicação no texto.A imagem central (número 4 na figura 3), com fundo branco, seria aquela obtida com "erro zero". As outras, com fundo cinza, representam seis tipos de erro que poderiam ter sido cometidos. Dificilmente o erro seria maior do que aqueles representados nos extremos da figura (números 1 e 7). Por outro lado, a imagem central (4) fica representada na tela de seu computador durante um certo intervalo de tempo bem superior a zero segundos e longe de ser realmente instantânea, o que seria de se esperar para uma distribuição contínua de imagens. Qualquer erro que você cometa, mas que esteja dentro desse intervalo de tempo, deixará de ser computado (será considerado como acerto), o que não ocorreria no caso da fotografia do movimento real de um automóvel [4].
Sob certos aspectos poderíamos dizer que, nos gifs animados, os "objetos" ocupam o espaço de uma maneira quantizada. O valor e o caráter dessa quantização estariam a critério do construtor da simulação. Fatores limitantes seriam tanto a qualidade do software utilizado quanto também a qualidade do computador que irá decifrar o que foi produzido neste software. Nos softwares produtores de vídeo podemos efetuar uma superposição sequencial de imagens de maneira tal que a movimentação em saltos não seja percebida pela nossa visão.
Movimento de um objeto implica na suposição de que o objeto ocupa lugares diferentes em tempos diferentes. Na vida real isto se dá, via de regra, de maneira contínua [5], tanto no espaço (ocupação espacial) quanto no tempo (ocupação temporal). Consequentemente, iremos muitas vezes raciocinar como se estivéssemos frente a essas realidades (continuidades), ainda que utilizando simulações (gifs animados) ou equipamentos (régua de tela e cronômetro digital, por exemplo) dotados de características discretas.
Para o estudo do movimento de um objeto torna-se necessário o conhecimento de pelo menos duas variáveis (o lugar ocupado pelo objeto e o instante em que ocorre essa ocupação) em pelo menos duas condições. Ou seja, deveremos trabalhar com um mínimo de quatro valores distintos, e tantos mais quanto mais sofisticado for o nosso estudo.
O gif animado 02 (vide abaixo) mostra uma bolinha que viaja na tela do seu computador da esquerda para a direita. Em um certo momento (ou em um dado instante ou, ainda, em um "ponto" determinado do tempo) a bolinha passa por um quadrado vermelho e, em outro momento, passa por um quadrado verde.
gif animado 02:
si sfDeixemos de lado, por ora, possíveis considerações sobre o tempo e vamos nos preocupar apenas com o espaço percorrido pela bolinha quando caminha do local onde se situa o quadrado vermelho até o local onde se situa o quadrado verde. O segundo desafio que lançarei será então o seguinte: Você seria capaz de medir o espaço percorrido pela bolinha na tela de seu computador nestas condições (ou seja, entre si e sf)? Antes que você pense em levar uma régua escolar até a tela de seu computador acrescento o mesmo que fiz no desafio anterior: "utilizando apenas os recursos que o seu computador possui" e mais: estou supondo que você ainda não possua uma "régua de tela" em seu computador. Este equipamento, que irá facilitar bastante o nosso estudo, será apresentado no capítulo 2. Procure agora resolver o desafio antes de prosseguir com a leitura.
A primeira coisa a ser feita você já deve ter desconfiado e nada mais é do que "fotografar" a tela do seu computador, num instante qualquer, contendo o gif animado 02. O instante pode ser qualquer pois os objetos de interesse (quadrado vermelho e quadrado verde) estão em repouso. Coloque então o gif animado numa posição conveniente e pressione a tecla PrtScr.
A seguir abra o Paint que certamente deve estar instalado em seu computador e muito provavelmente você já deve ter utilizado inúmeras vezes. Caso não, e se estiver tendo dificuldades para abrir o Paint, você poderá encontrar um atalho através do caminho que começa pelo botão Iniciar da barra de tarefas e prosseguir pelo caminho seguinte [Válido para o Windows XP — No caso do Windows Vista vide acima o último parágrafo do item 1.2]: Todos os Programas/Acessórios/Paint. Outra maneira seria procurar pelo arquivo mspaint.exe que deve estar na pasta C:/WINDOWS/system32 [Ü clicando aqui é possível que pasta se abra no seu computador — se não, copie o atalho (botão D do mouse) e cole ou no endereço do navegador ou no Windows Explorer].
Após abrir o Paint clique no menu Editar e logo a seguir em Colar. A imagem da área de transferência, com a "fotografia" do gif animado 02, será copiada para o Paint. Clique agora na ferramenta Linha
que deve estar à esquerda da janela do Paint. Agora o ponteiro do mouse deverá assumir um formato chamado seleção de precisão
. Procure, com este ponteiro, focalizar o pequeno quadrado vermelho do gif animado, centralizando o mais que puder o mouse neste quadrado. Você deverá visualizar algo deste tipo: Þ
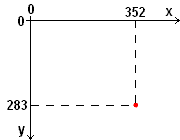
. Com o mouse nesta posição, procure por dois números que devem estar na borda inferior direita da janela do Paint, muito próximos da barra de tarefas do Windows, como os números 352 e 283 mostrados na figura 4 abaixo. [Se por acaso os números não estiverem aparecendo na tela do seu computador, clique em Exibir, no menu do Paint, e logo a seguir em Barra de status.] Leia esses números e anote seus valores.
Figura 4: Explicação no texto.Esses números são as coordenadas (x, y) da posição do ponteiro do mouse e cujo (0,0) está no cruzamento entre a primeira linha horizontal da janela do Paint (situada imediatamente abaixo da borda superior) com a primeira linha vertical (situada à esquerda). A unidade utilizada é o pixel (pix) que será estudado no capítulo 2. A figura 5 ilustra a localização do ponto determinado em unidades pix.
Figura 5: Coordenadas cartesianas com unidades
e orientação que aparecem no Paint.Agora faça o mesmo para o quadrado verde, visualizando algo deste tipo: Þ
. Leia novamente os números e anote os novos valores. Poderiam ser, por exemplo, 653 e 282.
Temos então as coordenadas dos pontos centrais dos quadrados e que segundo as minhas medidas seriam:
x (pix) y (pix) Quadrado vermelho 352 283 Quadrado verde 653 282 Não se preocupe com o fato de y ser, ou não, ligeiramente diferente nos dois casos. Erro de medida é um assunto bastante complexo e que será discutido oportunamente e de uma maneira lenta e fracionada [6]. No final deste capítulo você terá um breve contato com este assunto que é bastante difícil mas que é também extremamente importante para os cientistas de todas as áreas.
A distância entre o quadrado vermelho e o quadrado verde será então 653 - 352 = 301 pix. Usando agora a convenção anteriormente considerada (s para qualificar a posição da bolinha), temos:
si = 0 pix e (1.1) sf = 301 pix. Ao mudar de variável x para s, promovemos também uma mudança na origem do eixo das abscissas (rotineiramente chamado como eixo dos x) correspondente a 352 unidades (pix, no caso).
Notar que Espaço Percorrido = Δs = sf - si = 301 pix.
Vamos agora ao penúltimo desafio deste capítulo. Você seria capaz de calcular o intervalo de tempo decorrido entre a passagem da bolinha pelo quadrado vermelho e a passagem pelo quadrado verde? As considerações efetuadas nos desafios anteriores permanecem válidas e estou admitindo que você não possua nenhum software sofisticado que seja capaz de medir intervalos de tempo e que não faça parte do Windows.
A tarefa não é das mais difíceis, principalmente se não estivermos interessados na precisão do método. É quase certa a existência de um relógio digital, com indicação em horas e minutos, e que está bem a sua frente. Para visualizá-lo é suficiente desviar o olhar para a canto inferior direito do seu computador (na barra de tarefas).
[Se por acaso ele não existir, faça o seguinte: Clique em um ponto neutro da barra de tarefas, com o botão direito do mouse e, em seguida, clique com o botão esquerdo em Propriedades. Na janela que se abre, e no item Área de Notificação, preencha o quadradinho que existe ao lado de Mostrar o Relógio. A seguir dê um OK, aguarde alguns segundos e o relógio aparecerá na sua barra de tarefas.]
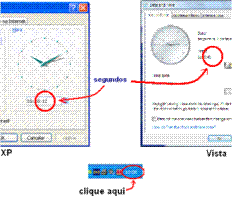
No "Windows XP" dê dois cliques rápidos nesse relógio digital. [No "Vista" dê um clique simples e a seguir clique em "Alterar data e configurações de tempo".] Com isso você abrirá uma janela intitulada "Propriedades de Data e Hora" (XP) ou "Data e Tempo" (Vista) e que contém, além de outras coisas, um outro relógio digital com precisão em segundos (figura 6).
Figura 6: Explicação no texto.Isto será suficiente por ora. Com esta janela aberta e com o gif animado 2 que, para sua comodidade, está reproduzido abaixo, você poderá fazer uma "estimativa grosseira" do intervalo de tempo considerado.
gif animado 02:
si sfArrume convenientemente as duas janelas [a do seu navegador e aquela que você acabou de abrir e que contém o relógio] a fim de que você possa enxergar tanto o relógio digital quanto o gif animado. Procure deixar o gif animado e o relógio próximos um do outro. Olhando para o gif animado 02, espere pelo momento exato em que a bolinha passa pelo quadrado vermelho. Quando isso acontecer, desvie rapidamente o olhar para o relógio e anote mentalmente os segundos lidos (fiz isso agora e obtive o valor de 11s). Retorne a seguir para o gif animado e repita o procedimento no exato momento em que a bolinha passa pelo quadrado verde (fiz isso agora e obtive o valor 15s). A seguir subtraia mentalmente o segundo valor do primeiro e você obterá uma estimativa grosseira do intervalo de tempo. No caso exemplificado este intervalo seria:
Δt = tf - ti = 15 - 11 = 4s
Clique ao lado para ir para o item 1.7 Þ
- Considerações sobre a metodologia net-in poderão ser encontradas no artigo Experiência de uma revista interativa na Internet.
- Um artigo bastante "soft" e relacionado à relatividade você poderá consultar clicando aqui: "O que é relatividade?". Aspectos relacionados ao absolutismo do movimento são comentados em O movimento absoluto e a física de Newton.
- Para mais detalhes sobre a área de transferência vide Capturando telas e janelas.
- Na realidade existe, no caso das fotografias, um pequeno intervalo de tempo em que o diafragma da máquina fica aberto, mas este é praticamente desprezível quando comparado com aquele que estamos considerando no momento.
- O "via de regra" está sendo empregado apenas para dar margem a que se pense também nos fenômenos estudados em física quântica, especialmente aqueles onde se admite que partículas elementares podem saltar de um lugar para outro sem ocupar, em nenhum momento, posições intermediárias.
- Caso você pretenda se adiantar no assunto, existe na Internet artigos elementares e bastante razoáveis, relacionados tanto à estatística quanto à teoria dos erros. A título de ilustração, indicarei os seguintes: 1) Guia Para Física Experimental - Caderno de Laboratório, Gráficos e Erros - Unicamp; 2) Teoria dos Erros. 3) Estatística de Contagem e Propagação de Erro. 4) Wikipédia - Teoria dos erros. 5) A Incerteza.
Advertência: Procure agir com ponderação e, principalmente, juízo crítico, mas sem se intimidar. Às vezes aprende-se mais criticando um mau artigo (não é o caso dos artigos citados) do que aceitando, de maneira dogmática, aquilo que determinado autor procura nos impingir como verdade absoluta, ainda que escrito nos moldes a satisfazer os critérios acadêmicos.