Estudo do Movimento
Estudo do Movimento
através da Metodologia Net-In
Alberto Mesquita Filho
Página 7
Capítulo 3 - 1ª Parte
Capítulo 3: Movimentos Uni, Bi e Tridimensionais
O mundo em que vivemos é, sob o ponto de vista espacial, tridimensional. Qualquer tentativa em caracterizar mundos com uma ou duas dimensões espaciais tem muito de ilusória. O plano, por exemplo, presta-se a dividir um espaço tridimensional em outros dois espaços tridimensionais, mas o plano em si não ocupa lugar em nenhum desses três espaços considerados. Se bem que semelhantes, não se deve confundir um plano geométrico com a parede de uma casa. A parede é tridimensional, enquanto que o plano é adimensional. O mesmo se diga com relação a uma linha reta (adimensional) e uma corda esticada (tridimensional). Em suma: não existem objetos unidimensionais nem bidimensionais. E "objetos" adimensionais existem apenas em nossa imaginação.
Uma folha de papel tem uma espessura finita e não nula. A tela do computador tem uma estrutura um pouco mais complexa, mas também forma imagens graças a determinados artefatos coerentes com uma espessura finita, pois do contrário a tela seria totalmente invisível. As sombras, assim como as projeções cinematográficas, são, pelo menos em teoria, adimensionais. Na prática, não obstante, conseguimos observar essas imagens graças às irregularidades dos objetos e que permitem a sua expressão sob formas visíveis. Uma tela de cinema, sob o ponto de vista físico, pertence muito mais à categoria das paredes do que à categoria dos planos geométricos.
Outro conceito importante é o de ponto, também adimensional e, portanto, sem existência física, ainda que de existência matemática. Os tratados de geometria costumam dizer que ponto, reta e plano não têm definição, e eu acrescento: sequer têm existência física. São meros artifícios matemáticos, ainda que extremamente úteis para o estudo da física e, em decorrência, para o estudo das demais ciências naturais.
Que dizer então sobre o título deste capítulo? Eu diria que apesar da realidade ser sempre tridimensional, ela comporta, em seu estudo, abordagens uni ou bidimensionais. Ou seja, a metodologia comporta a uni ou a bi dimensionalidade, a apoiarem-se em simplificações ou idealizações compatíveis com a geometria euclidiana. E esta metodologia acompanhará o estudioso do assunto não apenas no estudo dos movimentos, mas em inúmeros outros capítulos da física.
Frente ao rigorismo, mas sem renunciar ao uso de idealizações logicamente permitidas e compatíveis com a descrição da realidade física, vamos evoluir na tentativa de caracterizar aspectos subjacentes a essa metodologia. Vejamos inicialmente como os dicionários encaram um importante conceito, o de trajetória, assunto a ser abordado com mais propriedade no próximo item. O dicionário disponível no meu computador é o Houaiss [1] e, sob a rubrica física, ele diz o seguinte:
- Trajetória: "caminho percorrido por um corpo ou partícula em movimento."
Que dizer da distinção entre corpo e partícula? Partícula não seria caso particular de corpo? Não custa nada consultar o mesmo dicionário:
- Corpo: "tudo o que ocupa lugar; tudo o que tem existência física e extensão no espaço."
- Partícula: "corpo cujas dimensões e estrutura interna são irrelevantes para a análise e compreensão de um fenômeno físico."
Em outras palavras, sempre que nos for possível, e logicamente permitido, fazer a abstração das dimensões de um determinado objeto, estaremos caracterizando o objeto como sendo uma partícula, algo de natureza teórica e abstrata, mas que será extremamente útil "para a análise e compreensão de um fenômeno físico". Há que se distinguir esta "irrelevância" sob dois aspectos:
- Se, em determinadas condições, pudermos considerar as dimensões de um objeto desprezíveis, para a análise de um dado fenômeno, isto significa que o objeto está sendo encarado como adimensional, ou seja, como algo equiparável a um ponto geométrico. Por exemplo, podemos considerar a Terra puntiforme (partícula, no sentido acima definido), ao analisarmos o seu movimento ao redor do Sol. A órbita é tão grande em relação ao diâmetro terrestre que em muitos projetos de estudo essa idealização torna-se conveniente. Em outras palavras, sempre que os erros de medida estiverem acima da ordem de grandeza do volume dos objetos considerados, não perderemos nada ao tratá-los como puntiformes.
- Existe ainda o caráter "irrelevância" que nem sempre diz respeito às dimensões do objeto considerado. Para o estudo de um corpo rígido, ou indeformável, é comum fixarmos a atenção em algumas estruturas geométricas que os acompanham, como por exemplo, o centro geométrico (um ponto) ou um ponto da superfície geométrica e adimensional do corpo rígido e/ou alguns outros pontos particulares. Para determinados estudos não é impossível que o movimento de um ou mais desses pontos preste-se a representar todo o movimento do objeto. A estrutura restante do objeto passa por irrelevante, ainda que a sua extensão não seja desprezível em relação às medidas de comprimento efetuadas. Em grande número de casos é suficiente considerarmos apenas um desses pontos e, via de regra, mas não obrigatoriamente, costuma-se optar pelo centro geométrico do corpo rígido.
Por vezes costuma-se dar a essa abstração o nome de ponto material, se bem que a denominação esteja mais coerente com a metodologia utilizada no estudo dinâmico do movimento. Neste caso, nem sempre os elementos representativos acima sugeridos estão dotados das qualidades necessárias e inerentes ao conceito dinâmico, ainda que abstrato, de ponto material.
Para concluir o tópico, direi que se é verdade que a física presta-se a aceitar idealizações, sem colocar em risco o seu rigorismo, não é menos verdade que devemos tomar muito cuidado por ocasião das generalizações. Se pretendermos extrapolar os valores obtidos (ou os conceitos assimilados através da observação desses valores) para situações semelhantes, mas não exatamente idênticas, há que se analisar com extrema cautela as possíveis implicações decorrentes das idealizações previamente concebidas. Este é um trabalho de depuração de erros e que deve sempre ser efetuado, em especial pelos teorizadores.
As figuras 3.1 a, b e c ilustram o movimento de objetos virtuais segundo três possíveis trajetórias. Observando as ressalvas efetuadas no item 3.1, duas dessas trajetórias (a e b) podem ser consideradas como correspondendo a movimentos que ocorrem na tela do computador; já a terceira (c) denota um movimento em que a trajetória não se encaixa na tela do computador, a não ser como uma imagem em perspectiva. Comumente se diz que a representa um movimento unidimensional, b um movimento bidimensional e c um movimento tridimensional.
Figura 3.1 Movimentos em uma, duas e três dimensões a) trajetória retilínea b) trajetória circular c) trajetória helicoidal Nesta fase do nosso estudo quase sempre consideraremos os objetos como representativos de corpos rígidos (indeformáveis) e dotados exclusivamente de movimentos de translação. [A rotação de um corpo em torno de um ou mais de seus eixos poderá, ou não, vir a ser objeto de estudos futuros (não há nada planejado a esse respeito)]. Portanto não levaremos em conta possíveis rodopios dos objetos, seja em a (como efeito de derrapagens), seja em b ou em c (piruetas). Se há ou não esta rotação, ela poderá ser deixada de lado. De fato, e numa primeira instância, podemos ignorar a rotação da Terra em torno de seu eixo e considerar apenas o seu movimento de translação ao redor do Sol, como se a Terra fosse realmente um objeto puntiforme.
Além desses rodopios fortuitos, ou contingentes, pode-se pensar também na possibilidade do corpo rígido de alguma maneira se acoplar ou não à trajetória, à medida em que o movimento progride. Os motivos deste acoplamento (muitas vezes necessário para que o movimento possa ocorrer na prática) dizem respeito a conceitos que estão além daqueles estudados em cinemática; consequentemente serão, por ora, deixados de lado. Abordaremos apenas a natureza de alguns desses possíveis acoplamentos e como adaptar a existência desse acoplamento à metodologia inerente à cinemática.
Os movimentos representados na figura 3.1 (acima) estão dotados deste acoplamento, o que, para trajetórias planas e curvas (figura 3.1b), implicaria numa rotação segundo um eixo que acompanha o objeto de estudo e perpendicular à trajetória. A figura 3.2b (abaixo) demonstra como seria o mesmo movimento visto na figura 3.1b (reproduzido em 3.2a) sem o acoplamento referido. Nota-se em 3.2b apenas o movimento de translação do avião.
Figura 3.2 Explicação no texto a) vôo normal (idêntico ao da figura 3.1 b) b) vôo praticamente impossível Qualquer que seja o caso, e mesmo quando pudermos ignorar essas rotações, é importante notar que estamos perseguindo uma metodologia experimental, a diferir sobremaneira daquela apresentada na grande maioria dos livros didáticos. Ao efetuarmos medidas relacionadas a esses movimentos simulados e, observadas as dimensões do problema, se não pudermos considerar o objeto como sendo puntiforme, teremos de escolher um ponto representativo e a ser utilizado em todas as medidas pertencentes ao mesmo contexto experimental. No caso do automóvel da figura 3.1 a (movimento retilíneo) seria totalmente equivalente considerarmos como representativo um ponto situado na frente do automóvel ou, então, no centro de seu pneu dianteiro ou, ainda, na sua traseira etc. [O importante a ser observado é que uma vez efetuada a escolha, esta referência se mantenha a mesma.] O mesmo não pode ser dito para o avião das figuras 3.2 a e b (movimento circular). Dependendo do ponto considerado, a trajetória poderá não coincidir ou não se igualar àquelas mostradas nas figuras (casos 3.2 a e 3.2 b). Isso pode ser facilmente constatado, a ponto de permitir, tomando-se os devidos cuidados, o estudo do movimento desprezando-se ou não a existência de uma rotação do objeto e a acoplar-se à trajetória.
3.4 Dimensões e sistemas de coordenadas espaciais
Parece-nos mais ou menos óbvia a idéia de que o mundo em que vivemos é tridimensional, como assumido no item 3.1. Não obstante, nos primórdios da física atual houve quem se preocupasse em encontrar razões matemáticas que pudessem ou justificar ou desmistificar esta obviedade (mesmo porque nem tudo o que é óbvio é certo). Ao que parece Galileu foi o primeiro a estabelecer uma justificativa matemática, e a comprovação [2] está intimamente relacionada à utilização de um artifício muito semelhante ao sistema de coordenadas de Descartes.
Frente ao sistema de coordenadas cartesiano, podemos considerar que movimento unidimensional seria aquele em que todos os pontos representativos do objeto em consideração permanecem em uma mesma reta, que pode ou não coincidir com os eixos do sistema. Se os pontos permanecerem em um mesmo plano, mas não numa mesma reta, o movimento será bidimensional. Se os pontos não permanecerem em uma mesma reta e nem num mesmo plano, o movimento será tridimensional.
Nada obsta a que se justifique a tridimensionalidade espacial através de um raciocínio semelhante àquele proposto por Galileu mas utilizando-se de outros sistemas de coordenadas, por exemplo, um sistema curvilíneo qualquer. Frente a essa nova realidade, o movimento unidimensional poderia vir a ser definido como aquele em que os pontos representativos do objeto em consideração permanecem em uma curva muito especial e conforme com o sistema utilizado. Ou seja, mais uma vez, e por motivo diverso do apresentado anteriormente (primeiro parágrafo do item 3.2), o conceito unidimensional mostra-se estar mais associado à metodologia utilizada do que propriamente a uma existência real e caracteristicamente imutável.
Sob esse aspecto, e uma vez conhecida a trajetória, qualquer movimento poderia ser estudado sob o prisma da unidimensionalidade. Seria suficiente dispormos de métodos para medir o comprimento dos arcos de trajetória correspondentes às distâncias percorridas pelos objetos em dados intervalos de tempo. Isto nem sempre é fácil de ser feito e, em função disso, a abordagem unidimensional chega a ser pouco utilizada para o estudo de movimentos cujas trajetórias não são retilíneas. Uma exceção importante é a do movimento circular, pois é relativamente fácil medir o comprimento de arcos de circunferência de raios conhecidos (ver exercícios 2.4 e 2.5 do capítulo 2).
Outro fator limitante à utilização da abordagem unidimensional para movimentos coplanares e não retilíneos é que a trajetória normalmente não é conhecida de antemão, impondo-se a determinação das posições do objeto através de duas coordenadas. Ou seja, a abordagem unidimensional somente poderá ser levada a efeito após determinarmos a trajetória, e nem sempre este é o caminho mais adequado para o estudo que se pretende realizar.
O fator mais importante, a privilegiar tanto as abordagens bidimensionais (para movimentos no plano) como as tridimensionais (para movimentos no espaço tridimensional), relaciona-se aos princípios da mecânica (leis de Newton) e que são estudados em dinâmica do movimento. Não obstante, e já que um dos objetivos deste estudo é fornecer alguns requisitos para que o leitor possa vir a compreeder com mais facilidade a dinâmica do movimento, convém que nos familiarizemos com essas abordagens o quanto antes.
3.5 Exemplificando a abordagem bidimensional. Mais um desafio.
O gif animado 04 ilustra o movimento de um objeto virtual seguindo, aparentemente, uma linha reta e inclinada em relação às bordas do vídeo. Seria perfeitamente possível efetuarmos o estudo utilizando a metodologia unidimensional, de maneira bastante semelhante àquela efetuada no capítulo 2 (com o gif animado 03). No entanto, em virtude da inclinação e do desconhecimento prévio da trajetória, a abordagem bidimensional parece ser a mais conveniente.
O procedimento inicial é exatamente o mesmo descrito nos parágrafos quinto e sexto do item 2.4 (capítulo 2). Para esta etapa serão necessários o multiplicador da área de transferência e o cronômetro de tela. Caso não possua um cronômetro de tela utilize o cronômetro net-in clicando aqui e enfrente mais este desafio, qual seja, o de caracterizar e analisar o movimento apresentado no gif animado 04.
gif animado 04:
Obtidas as imagens, o procedimento será bastante semelhante àquele efetuado anteriormente. As principais diferenças relacionam-se:
- à maneira de configurar a régua;
- ao número de leituras (cada medida comporta 3 leituras: x, y e t); e
- à correspondente construção da tabela no Excel, agora com quatro colunas (i, t, x e y).
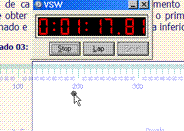
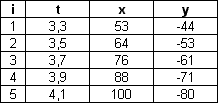
Troque o sinal do valor lido para y, pois na régua de tela o eixo cartesiano dos y é orientado para baixo e, para a nossa análise, convém orientá-lo para cima (Isto não é obrigatório, apenas, e como eu disse, conveniente). A figura 4 ilustra a disposição da régua e do cronômetro, e a tabela 3.1 mostra como os dados poderiam ter sido registrados no Excel.
Figura 3.4 Tabela 3.1 Possível disposição da
régua e cronômetro.Disposição, no Excel, das
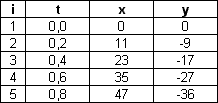
cinco primeiras medidas.Por questão de facilidade, convém mudar a origem do sistema de coordenadas espaço-temporal, de maneira a que a primeira medida seja (x, y, t) = (0, 0, 0). Para todos os valores da tabela deverão ser adicionados ou subtraídos um valor que será o mesmo para os elementos de uma mesma coluna. No caso da tabela 3.1 isso é feito subtraindo-se 3,3 de todos os elementos da coluna t, subtraindo-se 53 de todos os elementos da coluna x e adicionando-se 44 a todos os elementos da coluna y. Isso poderá ser obtido com extrema facilidade configurando-se a primeira linha da nova tabela em função dos dados da tabela primitiva, com as devidas correções e, a seguir, utilizando o recurso de arraste na vertical. A nova tabela será então:
Tabela 3.2
t em segundos, x e y em pixels.
Incerteza estimada de x e y = ± 1 pixestando aí representadas apenas as cinco primeiras medidas.
Após construir a tabela 3.2 dê um nome à planilha do Excel que está sendo utilizada e salve o arquivo. Procure organizar os dados como sugerido no item 2.6 e, procedendo de maneira semelhante àquela indicada no item 2.7, obtenha o gráfico das funções x = f(t) e y = g(t).
Seguindo o proposto no item anterior você deve ter obtido as duas funções, x = f(t) e y = g(t), expressas de duas maneiras: 1) tabela; 2) gráficos de "dispersão" do Excel. Abaixo temos o gráfico correspondente, construído no Paint, para os dados da função x = f(t) da tabela 3.2 (cinco primeiras medidas).
* * * * *
◄▬ Para voltar ou avançar clique nas figuras ▬►
- Dicionário Eletrônico Houaiss da Língua Portuguesa, Versão 1.0, Dezembro de 2001, Editora Objetiva Ltda.
- GALILEI, Galileo (1632): Dialogue concerning the two chief world systems, The Modern Library, New York, 2001, pp. 12-5.