Estudo do Movimento
Estudo do Movimento
através da Metodologia Net-In
Alberto Mesquita Filho
Página 8
Capítulo 3 - 2ª Parte
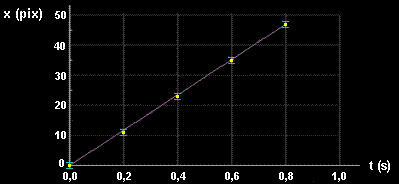
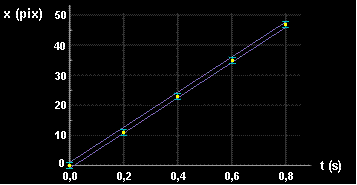
Seguindo o proposto no item anterior você deve ter obtido as duas funções, x = f(t) e y = g(t), expressas de duas maneiras: 1) tabela; 2) gráficos de "dispersão" do Excel. Abaixo temos o gráfico correspondente, construído no Paint, para os dados da função x = f(t) da tabela 3.2 (cinco primeiras medidas).
Figura 3.5: Explicação no texto.Além dos cinco pontos em amarelo, vê-se aí, em azul, uma das maneiras como poderíamos representar a incerteza nas medidas de x (no caso, a incerteza foi estimada em ± 1 pix). A reta em roxo foi construída unindo-se o primeiro ponto do gráfico (0; 0) ao último ponto (0,8; 47). Embora esta reta não tenha sido construída com o rigor necessário para que represente a "curva" mais provável a exprimir a função x = f(t), ainda assim ela se mostra como uma estimativa bastante razoável. E tanto é razoável que todos os cinco intervalos de incerteza contemplam pontos pertencentes a essa reta (vide figura 3.5) [Isto não garante mas sugere que a incerteza de ± 1 foi bem estimada].
Dificilmente você conseguirá exprimir os intervalos de incerteza nos gráficos construídos no Excel, mas isso não deve preocupá-lo pois estamos trabalhando com um caso muito particular, onde os intervalos de incerteza são bastante estreitos (praticamente confundem-se com a espessura dos "pontos" do gráfico do Excel). Por outro lado, os gráficos que você construiu, ou irá construir, devem ter uma extensão bem maior do que aquela mostrada na figura 3.5. Ora, ao expandirmos o domínio da função representada no gráfico, mantendo as dimensões do gráfico, promovemos, concomitantemente, uma redução no comprimento da unidade da escala dos eixos. Neste caso seria difícil exprimir a incerteza até mesmo com o gráfico construído no Paint. Em casos como esse a incerteza deve sempre acompanhar os resultados, mas isso pode se restringir a uma citação, como mostrado na tabela 3.2 (página 7).
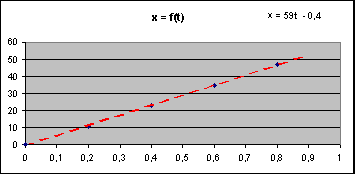
O próximo passo será encontrar a função contínua que melhor se ajusta aos pontos do gráfico. Para o Excel do Office 2007, clique com o botão D do mouse em um dos pontos do gráfico e a seguir em "Adicionar Linha de Tendência". Em "Tipo de Tendência" marque "Linear", na porção inferior da janela marque "Exibir equação no gráfico" e dê OK. [Para versões anteriores do Excel clique no gráfico correspondente à função x = f(t). O menu principal do Excel se modifica, aparecendo aí a categoria "Gráfico". Clique em Gráfico e, a seguir, em "Adicionar linha de tendência...". Na janela que se abre clique em "Tipo" e, a seguir, clique na figura situada acima de onde se lê "Linear"; em "Opções" assinale "Exibir equação no gráfico" e a seguir dê OK.]
Observe as modificações no gráfico correspondente. Escolha uma posição adequada para a equação. Modifique a equação substituindo y por x e x por t. Abaixo está o gráfico correspondente aos cinco pontos da função x = f(t) da tabela 3.2.
Figura 3.6A "equação da linha de tendência" do Excel na realidade é a equação da reta que está representada no gráfico (figura 3.6) em vermelho, e que surge como candidata a melhor representar a função contínua x = f(t) que estamos procurando. Sem entrar em maiores detalhes por ora, direi apenas que o Excel realiza esta proeza utilizando de um artifício que é descrito nos livros de Estatística e/ou de Cálculo Numérico como "aproximações de funções pelo método dos mínimos quadrados" [1]. Como todos os pontos contribuem com um peso significativo para a determinação desta reta, não estranhe o fato dela não passar exatamente pela origem do gráfico (no caso considerado ela passa 0,4 pix à esquerda do ponto (x, t) = (0, 0).
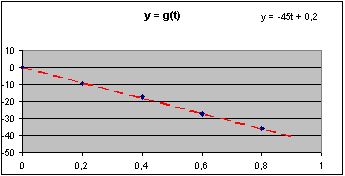
Observe agora o gráfico da função y = g(t). A simples inspeção do gráfico sugere uma linearidade, portanto o procedimento deve ser semelhante àquele efetuado para a função x = f(t). A figura 3.7 mostra o gráfico correspondente construído com os cinco pares de valores (y, t) da tabela 3.2.
Figura 3.7Estamos frente às funções x = f(t) e y = g(t) expressas de três maneiras distintas:
- tabelas;
- gráficos; e
- equações.
As tabelas apresentam os dados observados (experimentais); os gráficos clamam por uma expansão teórica dos dados experimentais, rumo à caracterização de um comportamento contínuo (idealização); e as equações se propõem a caracterizar matematicamente essa idealização. Sob certos aspectos poderíamos dizer que chegamos ao final de uma etapa experimental. Não obstante, a situação é um pouco mais complexa, haja vista que o final de uma etapa experimental coincide, quase sempre, com o início de um novo trabalho, por demais extenso e investigativo. Resumindo, não basta encontrar uma equação a se acoplar a um dado fenômeno; há que observar também, dentre outras coisas, até que ponto as idealizações efetuadas se justificam e/ou se prestam como fatores significativos e a apoiar a teorização. Na fase introdutória em que ora nos encontramos, os fatores a apoiarem a teorização poderão parecer pouco relevantes, mas isso deixará de acontecer à medida em que você for progredindo no estudo da mecânica desde que conserve uma atitude investigativa.
3.7 Significado das funções x e y
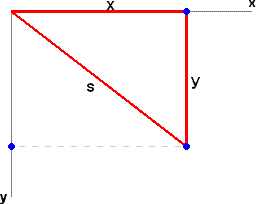
As funções expressas na tabela 3.2 [x = f(t) e y =gf(t)], representam as coordenadas (x,y) da posição do objeto virtual de nossa experiência, assumido como puntiforme. Estando o objeto em movimento, essas coordenadas vão se modificando no decorrer do tempo. Tudo se passa como se os pontos que representam essas coordenadas se movessem de maneira acoplada com o objeto. Esta movimentação complexa simula uma projeção ortogonal do movimento do objeto na direção dos eixos x e y, como mostra a figura 3.8.
Figura 3.8 Figura 3.9 A figura 3.9 acrescenta alguns detalhes mais ou menos óbvios e a relacionarem as coordenadas x e y com s, a distância percorrida pelo objeto virtual ao longo de sua trajetória, entre a primeira medida e a medida efetuada após um certo tempo t (no caso da figura, a quarta medida da tabela 3.2). Nota-se claramente a possibilidade da determinação de s = f(t) aplicando-se Pitágoras, ou seja, através da relação s² = x² + y², válida para todos os pontos experimentais. Em outras palavras, a abordagem bidimensional (plano x,y) contém, como não poderia deixar de ser, as características unidimensionais do movimento.
Vamos agora às equações expressas nas figuras 3.6 e 3.7 (com x e y em pix e t em s):
x = 59t - 0,4 e y = -45t + 0,2
Convém mudar novamente a origem dos espaços, de modo a obtermos inicialmente (x, y, t) = (0, 0, 0). Facilmente verifica-se que isto ocorre para
x = 59t e y = -45t
(x e y em pix e t em s)Observação: Do ponto de vista físico esta modificação é sempre permitida. Não obstante, para o cálculo do desvio padrão deve-se utilizar a equação obtida através do método dos mínimos quadrados sem modificações (isto será observado no próximo item).
Aplicando Pitágoras, como sugere a figura 3.9, chegamos na equação de s:
s² = x² + y²
s² = (59² + 45²)t²
s² = 5506t²
s = ± 74,2tEscolhendo o sentido dos s positivos coincidente com o sentido do movimento, chegamos à equação procurada para a função s = f(t):
s = 74,2t
(s em pix e t em s).Esta é a equação horária do movimento, notando-se que é a equação de uma reta no "plano" (x,t) e, portanto, a sugerir que o movimento é uniforme (o objeto percorre distâncias iguais em tempos iguais), conforme comentado no item 2.7. Deixarei aqui uma questão a ser esclarecida oportunamente: Os erros experimentais afetaram as variáveis x e y (no caso a incerteza foi estimada em 1 pix para mais e para menos). Como propagar essa incerteza para as estimativas dos valores de s?
Com o auxílio das equações x = f(t) e y = g(t) pode-se também caracterizar a trajetória do movimento. Com efeito, essas duas equações são chamadas equações paramétricas de uma curva definida por y = F(x). O parâmetro no caso é a variável t e esta "curva" nada mais é senão a trajetória do objeto virtual que estamos estudando. Vamos então obter a equação da trajetória:
x = 59t ▬►
▌
▼y = -45t ▬► Como era de se esperar (movimento retilíneo), estamos frente à equação de uma reta com inclinação negativa e que neste caso, e por opção nossa, passa pela origem.
Importante: A equação horária [s = f(t)] caracteriza o movimento em função do tempo sem fornecer detalhes sobre o tipo de trajetória. Uma equação horária retilínea caracteriza a uniformidade do movimento, assim como determinados tipos de equações senoidais caracterizam a periodicidade do movimento (vide mhs). O movimento circular e uniforme, por exemplo, tem uma equação horária s = f(t) do mesmo tipo que aquela que estamos ora estudando. Quem caracteriza a trajetória é a equação da trajetória [do tipo y = f(x)].
3.8 Mais sobre erros e desvios
Ao efetuarmos medidas de variáveis correlacionadas, como fizemos nos itens anteriores, é costume considerar a medida da variável independente (no caso em consideração, a variável t) como exata (ou sem erros). Isto não é equivalente a uma desconsideração do erro, mas sim a uma transferência desse erro para a estimativa da variável dependente. Como então efetuar essa transferência? Por um lado, já comentamos algo nos capítulos anteriores e a relacionar-se com a subjetividade do método e/ou com a astúcia do experimentador. Por outro lado, e como veremos, nem mesmo esta subjetividade e/ou astúcia irão pesar significativamente no estudo dos erros, haja vista que estamos trabalhando com variáveis correlacionadas e a possibilitarem previsões matemáticas um pouco mais sofisticadas.
No capítulo 1, item 1.8, chamamos a atenção para uma sutil diferença entre erro e desvio. Vamos reproduzir uma dessas diferenças: "Quando estamos trabalhando com grande número de medidas, podemos deixar as considerações sobre erros de lado e pensar em desvios. Desvio seria "a diferença entre um valor obtido ao se medir uma grandeza, e o valor que estamos assumindo como aquele que mais se aproxima do valor real."
Á primeira vista não poderíamos aplicar esse conceito de desvio em nosso estudo atual, posto que, apesar de termos efetuado grande número de medidas, cada medida foi efetuada uma única vez. Não obstante, essas medidas estão todas correlacionadas, a ponto de nos possibilitarem o encontro de equações que exprimem matematicamente a correlação (o nome adotado em estatística para esta equação obtida pelo método dos mínimos quadrados é equação de regressão e, no caso específico, regressão linear). Aceitando essas equações como algo a nos fornecer "o valor que mais se aproxima do valor real", podemos obter os desvios referentes a todas as medidas efetuadas, tanto para x quanto para y. Não é rara a utilização do termo resíduo para esse tipo de desvio. O desvio, ou resíduo, seria então
desvio = valor obtido experimentalmente - valor obtido utilizando-se a equação.
Vamos chamar de xi (i = 1, 2..., n) os valores obtidos experimentalmente e de x'i os correspondentes valores (mesmo t) obtidos utilizando-se a equação x = 59t - 0,4 (conforme expresso na figura 3.6). Os desvios dxi serão então dados pela expressão:
dxi = xi - x'i (i = 1, 2..., n)
Os quadrados dos desvios serão então:
dxi² = (xi - x'i)² (i = 1, 2..., n).
O mesmo pode ser feito para yi e y'i, obtendo-se os correspondentes desvios dyi e dyi². Notar que a equação a ser agora utilizada é y = - 45t + 0,2.
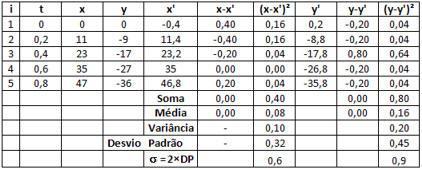
Promova agora uma expansão na sua tabela do Excel (correspondente à tabela 3.2 acima) acrescentando as colunas x', x-x', (x-x')², y', y-y', (y-y')² e, abaixo da tabela, os textos "Soma", "Média", "Variância", "Desvio Padrão" e "σ" como mostrado na figura a seguir e com os respectivos valores já calculados (Em dúvida clique aqui):
Tabela 3.3
Notar que a soma e a média dos desvios devem ser iguais ou bem próximas de zero [2] [Se tivéssemos desprezado os fatores -0,4 e +0,2 das equações para x' e y' respectivamente, esta igualdade (ou proximidade) poderia não ter sido obtida.].
Pode-se demonstrar [3] que ao assumirmos para a incerteza σ o dobro do valor do desvio padrão, esta incerteza cobrirá uma faixa correspondente a algo muito próximo de 95% dos valores obtidos experimentalmente.
Os valores obtidos para as incertezas concordam, mais uma vez, com o fato de a incerteza de ± 1 pix ter sido uma estimativa razoável. Há de se notar, não obstante, que estamos comparando dois tipos de incerteza conceitualmente distintos. Um deles relaciona-se à estimativa de erro em cada medida obtida individualmente, enquanto que o outro presta-se a caracterizar um intervalo em faixa, onde a maioria das medidas deveria se situar. A figura 3.10 ilustra essas diferenças para a variável x. Os pontos experimentais estão em amarelo, as incertezas individuais em azul. Em roxo são apresentadas duas retas a limitarem uma faixa correspondente à incerteza coletiva. Essas retas são x = 59t ± 1.
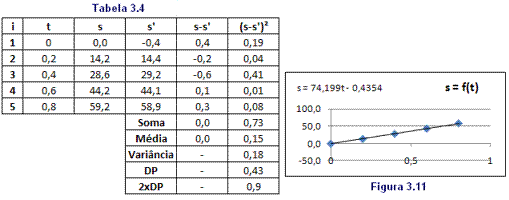
Figura 3.10Deixamos pendente, no item anterior, a questão da obtenção da incerteza para s. Aqui também poderíamos pensar em uma incerteza individual ou em uma incerteza coletiva. Nos dois casos elas poderiam ser obtidas através das equações de propagação de incertezas. Não obstante, e haja vista que é possível obter a equação de regressão para s, pode-se também obter a incerteza σs por procedimento semelhante àquele adotado para a obtenção de σx e σy na tabela 3.3.
Para o cálculo de s usar s2 = x2 + y2, com valores de x e y observados nas tabelas 3.2 ou 3.3. A seguir obtenha o gráfico de s = f(t) com esses valores de s e os correspondentes valores de t. No gráfico acrescente a equação de regressão (linha de tendência do Excel) e utilize-a para a construção da coluna s' (vide como exemplo a tabela 3.4 abaixo). A seguir e por procedimento semelhante àquele utilizado na construção da tabela 3.3 procure chegar ao valor de σs.
Fim do Capítulo 3
* * * * *
◄▬ Para voltar ou avançar clique nas figuras ▬►
- CASTRO HUMES, Ana Flora P.; Inês S. Homem de Melo, Luzia Kazuko Yoshida e Wagner Tunis Martins (1984). Noções de Cãlculo Numérico, McGraw-Hill, São Paulo, p. 93 e seguintes.
- Pequenas diferenças correm por conta da utilização de equações na forma aproximada.
- A demonstração está além dos objetivos deste trabalho, mas poderá ser encontrada na maioria dos livros de estatística.