Estudo do Movimento
Estudo do Movimento
através da Metodologia Net-In
Alberto Mesquita Filho
Página 5
Capítulo 2 - 2ª Parte
2.8 Tipos de erros experimentais
Costuma-se classificar os erros experimentais em três modalidades:
- grosseiros;
- sistemáticos;
- acidentais ou aleatórios.
Existem classificações mais amplas a incluírem outras modalidades, mas para o que nos interessa podemos nos limitar a essas três. Essas categorias comportam subdivisões. Às vezes nos interessa localizar o agente do erro (por exemplo, se o observador ou o equipamento) e, neste caso percebe-se que as três categorias comportam essa mesma subdivisão.
Não há muito o que dizer sobre erros grosseiros a não ser que, via de regra, podem ser reduzidos ou eliminados, seja através de uma medição cuidadosa (erros grosseiros do observador), seja através da aquisição de equipamentos mais refinados. Como vimos no capítulo 1, dependendo do objetivo do estudo pode-se trabalhar com equipamentos grosseiros e, ainda assim, tirar proveito das medidas efetuadas.
Erros sistemáticos são aqueles que, pelo menos em teoria [1], têm amplitude constante. Afetam os resultados sempre no mesmo sentido, para mais ou para menos. O experimentador pode estar dotado de vícios de posição, reflexos retardados etc. Um equipamento mal calibrado pode responder pela observação de erros desse tipo.
O erro sistemático, uma vez descoberto, presta-se a correções, o que pode ser feito com medidas efetuadas num passado recente ou até mesmo longínquo e de importância histórica. Num dos livros do TIPLER [2] existe um problema a explorar este efeito e a questionar "qual relógio seria mais apropriado para ser padrão secundário do tempo, aquele que adianta sempre 10% em relação ao padrão primário, ou aquele que atrasa, aleatoriamente, em apenas 1%". A resposta é mais ou menos óbvia e deixo como exercício. Se você retornar ao item 2.1 deste capítulo irá perceber que o erro que se comete com a régua de tela, ao se inferir distâncias em centímetros, também é desse tipo (sistemático), prestando-se a correções e recuperação dos valores observados.
Em certos casos o pesquisador utiliza-se de um ou de outro procedimento que poderia ou não se caracterizar como um tipo de erro sistemático. A título de exemplo, deixei subliminarmente um desafio no final do item 2.4 deste trabalho. Você conseguiu localizar o “suposto” erro aí cometido?
Se não vejamos: Quando você abre uma figura no Visualizador do Windows, se esta figura for muito grande, provavelmente ela não aparecerá no seu tamanho original. Ela surgira em um tamanho que é chamado como “Melhor ajuste”. As figuras que salvamos no item 2.4 tinham todas elas o tamanho da tela do computador, logo eram figuras grandes. Como efetuamos as medidas não no Paint, mas no Visualizador, os valores encontrados foram todos reduzidos por um fator constante (constante porque todas as figuras tinham o mesmo tamanho original). Em meu computador de mesa, por exemplo, uma distância de 500 pix em uma figura de tela cheia, acaba sendo reduzido para 436 pix, enquanto que em meu notebook este mesmo valor (500 pix) cai para 347 pix.
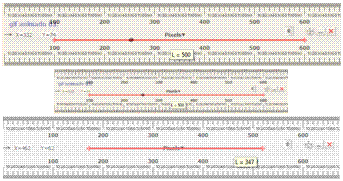
A figura 15 mostra, em sua parte superior, uma régua de tela efetuando uma medida real de 500 pix (Obs.: a figura 15 está em tamanho reduzido 50%) em uma figura bmp salva em tela cheia do meu Notebook. No centro mostro como esta mesma régua é observada no Visualizador do meu Notebook. E na parte inferior está representada a medida real daquela mesma distância, porém efetuada na figura em tamanho reduzido (e o valor encontrado é 347 pix).
Figura 15: Explicação no texto.Pode-se evitar este tipo de erro de quatro maneiras:
- Efetuando as medidas no Paint.
- Antes de efetuar cada leitura no Visualizador, dê um clique no botão “Tamanho Real” ou “ Actual Size”.
- Calcular o fator de correção para o seu computador e multiplicar todas as medidas por este valor (válido quando este valor é constante, como no caso exposto acima).
- Assumir o valor reduzido como sendo outra unidade de medida, por exemplo, pix* ou “pix red” (red = reduzido). Neste caso, e como o fator de correção varia de computador para computador, seu valor deve constar ao lado do conjunto de medidas.
Portanto, calcule o fator de correção em seu computador, retorne à planilha do Excel salva no item 4, explicite este fator, bem como o seu significado e substitua pix por “pix red” ou algo equivalente. Do contrário seus dados estarão contaminados por um erro sistemático. Perceba que para o desafio proposto [verificar se o movimento é ou não é uniforme] é indiferente medir s em pix ou em "pix red".
Os erros acidentais ou aleatórios são de vários tipos. Alguns desses serão apresentados em um ou outro exercício ou quando algum comentário se fizer necessário durante essa nossa breve jornada. Via de regra não podem ser eliminados por completo, ainda que, em alguns casos, possam ser atenuados. A metodologia utilizada na teoria dos erros, cuja importância venho enfatizando desde o capítulo 1, aplica-se a esses erros acidentais.
O cronômetro net-in funciona de maneira razoável, apesar de estar dotado de alguns inconvenientes, mas ele foi construído para ser acessado a partir de uma página web e, portanto, nem sempre estará disponível em seu computador. Convém promover a instalação de um cronômetro digital mais robusto e capaz de fornecer intervalos de tempo com a precisão de frações de segundos (pelo menos décimos de segundos). Não é difícil encontrar, em sites de pesquisa, cronômetros desse tipo. (Mais detalhes em nota de rodapé [3]).
Não há muito o que dizer a respeito do manuseio de cronômetros de tela pois, via de regra, esta é uma tarefa relativamente simples. Não obstante vou aproveitar o item para exemplificar um tipo de erro fácil de ser constatado e, consequentemente eliminado, e que ocorre esporadicamente quando utilizamos alguns desses cronômetros.
A tabela 2.2. abaixo exprime valores da função s = f(t) obtidos experimentalmente de maneira semelhante àquela apresentada nos itens 2.4 a 2.7, se bem que para um objeto virtual que se move de maneira diversa daquela apresentada nesses itens (o movimento não é uniforme). Na figura 15 temos o gráfico correspondente.
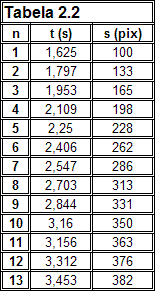
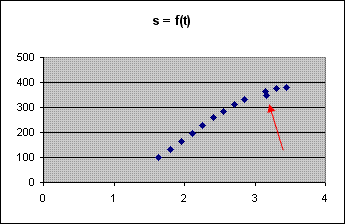
Tabela 2.2 e Figura 16. Na figura 16 tem-se o gráfico
da função s = f(t) expressa na Tabela 2.2.Chama a atenção neste gráfico o fato de termos obtido uma curva bastante regular. Em sua parte inicial ela é muito semelhante àquela apresentada na figura 13 (no caso uma reta), mas em sua parte final tende a um valor constante para s (próximo de 400 pix). Ou seja, o objeto virtual está tendendo ao repouso no decorrer do tempo, como se estivesse sendo brecado. Chama a atenção também o fato de que um dos pontos representativos da função, aquele assinalado com uma seta vermelha na figura 15, não obedecer a mesma regularidade observada para o conjunto dos demais pontos.
Observando o gráfico sob um ponto de vista puramente matemático não há como dizer se a anomalia observada é inerente à função ou se é devida a um erro experimental. Sob o ponto de vista físico, e apenas pela observação do gráfico, também não estamos autorizados a concluir por um erro. Afinal, nada impede que um objeto que esteja descrevendo um movimento aparentemente regular, subitamente modifique o seu estado de movimento (um abalo, ou um retorno súbito no caso) e logo a seguir volte a adquirir a regularidade anteriormente constatada.
Neste caso, no entanto, temos a história da experiência. Não apenas sabemos o significado dos termos s e t como também sabemos que os dados estão ordenados sequencialmente e da maneira como foram observados. Esta ordem está registrada na tabela 2.2. através do índice n. O ponto anômalo do gráfico corresponde à décima medida (n = 10). Curiosamente o tempo registrado em n = 10 não é um valor intermediário entre os tempos registrados em n = 9 e n = 11!!! Isso é muito estranho, pois entre as medidas 10 e 11 tudo se passa como se o cronômetro estivesse registrando um retorno no tempo!!!
Certamente, quando "fotografamos" (PrintScrin) o cronômetro em n = 10, por um motivo qualquer o cronômetro não estava registrando o tempo real. Esse tempo real deveria ser algo próximo de 3,0 s. Note que a média entre 2,844 e 3,156 é exatamente 3,000. Neste exato momento o relógio deveria estar modificando um de seus dígitos de 2 para 3 e, por um motivo desconhecido, os demais dígitos (após a vírgula) sofreram algum tipo de perturbação, de maneira que o tempo registrado não está correspondendo ao tempo real.
Embora esta falha seja uma característica do cronômetro utilizado, isso dificilmente irá prejudicar os seus trabalhos a ponto de você precisar escolher um outro cronômetro. Este é um fenômeno muito fugaz e dificilmente irá ocorrer em seus estudos, da maneira como aconteceu no caso acima relatado. Note, pela tabela 2.2, que entre as medidas 3 e 4 (n = 3 e n = 4) também ocorreu a mudança do primeiro dígito (de 1 para 2) mas as medidas não foram registradas no instante exato da mudança de dígito, mas sim um pouco antes e um pouco depois.
Este é um tipo de erro acidental diferente daqueles que costumamos classificar como erros aleatórios (final do item 2.8). Não há como corrigir este erro (ou assumir um outro valor para a medida), mas neste caso estamos autorizados a eliminar essa medida (n = 10) com a certeza de que não estamos cometendo nenhuma heresia. É importante realçar que esse tipo de conduta (eliminar um dado experimental) raramente se justifica e na maioria das vezes temos que conviver com esses pontos aparentemente anômalos. Muitas vezes anomalias como esta ocorrem de fato, e não como erro experimental, cabendo ao cientista não apenas documentá-las, com o sentido de divulgar o achado, como também tentar encontrar uma possível explicação para o fenômeno.
Fim do Capítulo 2
* * * * *
Para voltar ou avançar
◄▬ clique nas figuras ▬►
* * * * *
- Digo em teoria porque o assunto é um pouco mais complexo. Às vezes, o que faz com que esse erro não seja exatamente constante, diz respeito a algo que se encaixa na categoria dos erros acidentais ou aleatórios. Ou seja, existiria um erro acidental observado na estimativa (ou na medida) do erro sistemático.
- TIPLER, Paul A. Física para cientistas e engenheiros, Volume 1, 4ª. Edição (tradução), LTC Editora, Rio de Janeiro, p. 14.
- Eu utilizo o Virtual Stopwatch v3.18 que pode ser adquirido em http://www.springcreeksoftware.com/ [quando esta nota foi escrita o cronômetro custava $15.00]. Não obstante, existem excelentes cronômetros frewares, é questão de procurar.