II.1 - A luz ondulatória de Huyghens

A idéia de luz ondulatória tem muito a ver com a noção intuitiva de onda mecânica e, em especial, com a propagação de vibrações em meios fluidos como o ar ou a água. Christian Huyghens (1629-1695), ao conceber a luz ondulatória, não se fez de rogado e, ao dar conta da propagação da luz no vácuo, assumiu a existência de um éter a permear o universo.

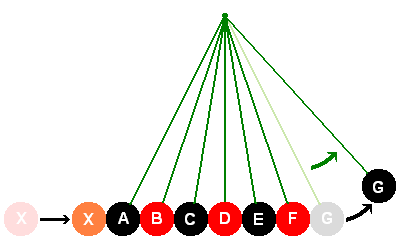
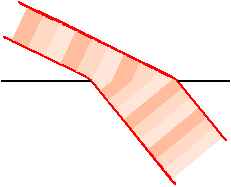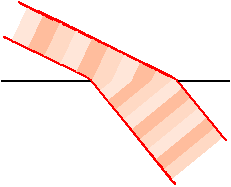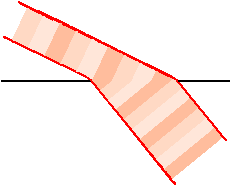
É importante perceber que a idéia de luz ondulatória surgiu num contexto bem diferente do atual. Com efeito, e a despeito dos trabalhos de Boyle (1658) e Bernouilli (1738), a noção de matéria constituída por partículas elementares a se instalarem no vazio (ou no vácuo de Torricelli, 1644), somente começou a ser levada a sério a partir dos trabalhos de Clausius (1857), Maxwell (1875) e Boltzmann (1860), a fornecerem as bases para as teorias atômicas da física atual [1]. Até a segunda metade do século XIX, os meios assumidos como sede dos fenômenos ondulatórios, quais sejam, o ar a propagar o som e a água a transportar momento (ou movimento), eram, via de regra, assumidos como fluidos contínuos. Até mesmo a analogia macroscópica, devida a Huyghens [2] (Figura 7), conquanto corpuscular em essência, assume uma continuidade absoluta e inerente a esse meio de propagação de impulso (esferas enfileiradas e em contato íntimo).

Figura 7: A transmissão de uma perturbação (onda), através de um meio intermediário, se assemelha a uma colisão entre bolas, que transmitem sucessivamente o movimento. Adaptado de ilustração do Traité d'Óptique de Huyghens, apud Franco [2].

Rigorosamente falando, e sem demérito algum ao trabalho de Huyghens, sua teoria é incapaz de dar conta até mesmo da explicação da natureza íntima das ondas mecânicas, como as conhecemos hoje [3]. Que dizer da luz ondulatória?

Sabemos hoje que as moléculas não dão trombadas, na acepção macroscópica do termo. Os choques entre partículas elementares, átomos e moléculas, dão-se a distância, por menor que seja essa distância. Até mesmo os fenômenos ondulatórios bem conhecidos exigem que alguma coisa passe de um corpúsculo para outro a distância. E o que seria essa alguma coisa senão o espírito da matéria invocado por Newton (vide item I-2)? Ou seja, a onda mecânica clássica (por exemplo, a onda sonora ou a onda aquática) existe se, mas somente se, as partículas que vibram emitirem alguma coisa capaz de sensibilizar as partículas vizinhas, bem como sofrerem uma retroação. Até mesmo na figura 7 (acima) isso deve estar ocorrendo em nível elementar (e não só entre as esferas, mas também no interior das mesmas, entre suas partículas constitutivas). Logo, a dualidade é inerente às ondas mecânicas clássicas, havendo pois um fenômeno ondulatório, observável macroscopicamente, acoplado a uma emissão de uma entidade pertencente ao microcosmo, provavelmente imaterial em essência e do mesmo tipo daquela que responde pela gênese dos campos gravitacional [4], elétrico e magnético. Mas... e no caso da luz?

II.2 - A refração de Descartes

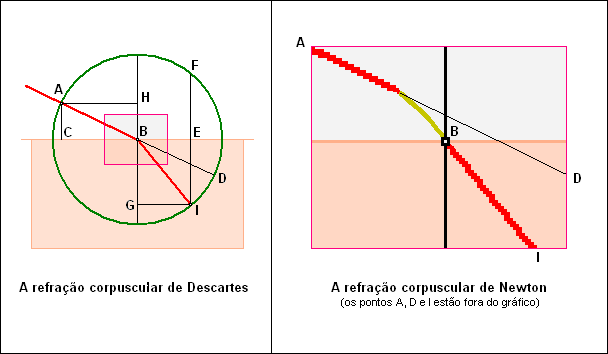
Uma das experiências marcantes a dar o veredicto do século XIX à luz ondulatória, foi aquela realizada por Foucault (1850), ao constatar que em meios opticamente densos a luz propaga-se em velocidades menores do que no vácuo. Os físicos dessa época aceitavam a lógica de Descartes (1637) [5], segundo a qual a curvatura da trajetória de um corpúsculo de luz ao passar do ar para o vidro, seria devida a uma força perpendicular à superfície CE, conforme a figura 8a, e dirigida para o segundo meio (vidro no caso).

Figura 8: a) A refração corpuscular de Descartes; b) A refração corpuscular de Newton.

Esta mudança de direção (de AB para BI na figura 8) não deveria ser instantânea ou brusca e a ocorrer exatamente no ponto B. Provavelmente seria gradativa, como descrito por Newton na questão 4 de sua Óptica III (op. cit., vide referências do capítulo I): Os raios de luz, que incidem nos corpos e são refletidos ou refratados não começam a se curvar antes que cheguem aos corpos? A figura 8b, ampliação idealizada (mas não em escala) do pequeno retângulo central da figura 8a, exprime essa idéia. Essa figura estaria em acordo com um ganho em velocidade dos corpúsculos, pois a curvatura dar-se-ia, sem dúvida, através de uma força de atração exercida pelo vidro. Mas... a experiência de Foucault demonstrou exatamente o contrário, qual seja, a menor velocidade da luz no segundo meio em relação à velocidade da luz no primeiro meio. Seria a luz realmente ondulatória? E, neste caso, a mudança de direção seria brusca, como proposto pela teoria ondulatória? Haveria, nas vizinhanças do ponto B (figura 8a) uma inflexão brusca, ou melhor, uma quebra da "frente de onda", como mostrado na figura 9 e como defendem os adeptos da teoria ondulatória?

Figura 9: Refração ondulatória

Sabe-se hoje que essa história está mal contada. Entre um átomo e outro, de um meio opticamente denso, a luz propaga-se na mesma velocidade v com que entrou nesse meio, nem mais, nem menos. Acontece que durante a passagem pelo meio opticamente denso, a luz vai sendo alternadamente absorvida e reemitida (vide capítulo V, item V.4.1), tendo-se como resultado final uma redução da velocidade medida v_m da luz [6]. Esta seria, portanto, uma velocidade média v_m a contrastar com a velocidade real v. Existiriam então quatro velocidades em jogo: a) duas relacionadas a cada um dos meios 1 e 2, as velocidades médias v_1m e v_2m, correspondendo às velocidades medidas e a levarem em conta o tempo em que a luz permanece absorvida pelas partículas do meio; e b) duas velocidades reais, v₁ e v₂, a corresponderem às velocidades com que a luz percorre o trajeto entre uma partícula e a seguinte da trajetória do raio de luz. Se o primeiro meio for o vácuo teremos v_1m = v₁ = c. Do contrário, e sob um ponto de vista estritamente clássico, deveríamos ter sempre v_1m ¹ v₁ ¹ c.

Suponhamos então que o meio 1 seja o vácuo. Neste caso é interessante observar que as velocidades real e média (ou velocidade medida) do meio 2 relacionam-se entre si através do quadrado do índice de refração do meio 2 [Obtém-se a terceira equação mostrada na tabela abaixo multiplicando-se as duas primeiras membro a membro].

"Esperança" de Descartes	Lei de Snell-Descartes (após Foucault - 1850)	Relação entre velocidade real e velocidade média

A discussão dessas relações entre velocidades está além do objetivo proposto para este artigo, mas lembro que o que chamei "esperança" de Descartes seria válido para a luz corpuscular. Lembro ainda que é uma "esperança" puramente teórica e a não levar em conta outras possíveis interações entre a luz e a matéria, como comentado na referência 4 do capítulo I. É de se notar que assumindo-se a idéia de absorção e reemissão, para explicar a redução na velocidade, a teoria ondulatória fica a nos dever a explicação da mudança de direção dos raios de luz.

II.3 - Contradições à luz mecânico-ondulatória

É comum atribuírem a Malus (1809) a descoberta da polarização da luz, mas esse fenômeno, como vimos no item I-3, já era sobejamente conhecido por Huyghens e Newton, e atribuído a Erasmus Bartholine. Aliás, esse era um dos grandes trunfos apontados por Newton em defesa de sua teoria corpuscular e a complicar tremendamente a teoria ondulatória de Huyghens. Essa dificuldade foi reconhecida tanto por Huyghens, ao sugerir uma dualidade do éter (ou seja, dois meios vibrantes) quanto por Fresnel, ao assumir que "é preciso acumular no éter um grande número de propriedades muitas vezes de difícil conciliação" [7].

Uma segunda experiência a colocar em xeque a luz ondulatória foi efetuada por Michelson e Morley (1879) [8] [9]. Este foi, a meu ver, o xeque-mate, a ponto de não podermos mais falar hoje em luz ondulatória no sentido original do termo, ou seja, a luz como onda mecânica. A partir da experiência Michelson- Morley devemos pensar na luz ou como algo a se adaptar às teorias de emissão, podendo-se pensar em luz como "onda" eletromagnética, numa tentativa de acomodá-la com a física clássica (esse assunto será tema do capítulo III), ou então em algo a se incompatibilizar totalmente com a física clássica, caminho esse trilhado por Einstein [10], se bem que por outros motivos que não serão discutidos aqui.

III.1 - A luz ondulatória de Maxwell

O apogeu da teoria ondulatória da luz coincidiu com a publicação, por James Clerk Maxwell, de uma série de artigos (1855 a 1865) [1]. Durante a construção de sua teoria eletromagnética, Maxwell gradativamente foi se convencendo da existência de um hipotético éter eletromagnético, a comportar as linhas de força de Faraday. Este éter seria o responsável pela propagação de alguma coisa a que Faraday (1846) denominara radiação como uma vibração das linhas de força [1]. No seu tratado sobre eletricidade e magnetismo [2], publicado em 1873, Maxwell refere-se a essa radiação, proposta por Faraday, como propagação de ondulações em um meio não condutor. Chega então a deduzir uma fórmula a relacionar propriedades eletromagnéticas, definidas em sua teoria, com a velocidade V de propagação desses distúrbios eletromagnéticos, chegando então à seguinte expressão:

onde ε_o = permissividade no vácuo e µ_o = permeabilidade no vácuo (essas variáveis, foram adaptadas aos símbolos e nomes utilizados na atualidade; no original ε_o = K).

Como ε_o e µ_o são passíveis de determinação laboratorial, Maxwell utilizou-se dos valores dessas propriedades eletromagnéticas (ε_o e µ_o) conhecidas na época, chegando ao valor numérico de V. Concluiu então que V era da mesma ordem de magnitude da já determinada —por vários autores, e por métodos diversos e ópticos— velocidade da luz no ar ou no espaço planetário (vácuo).

Ao concluir sua teoria, Maxwell tinha plena convicção de que o éter eletromagnético seria o mesmo éter luminífero das teorias óptico-ondulatórias aceitas na época, mas é importante ressaltar que as ondulações eletromagnéticas eram encaradas, na época de Faraday e Maxwell, como hipóteses, ainda que descrevessem, com propriedade, distúrbios observados em um campo eletromagnético; somente em 1888 (quinze anos após a publicação do tratado de eletromagnetismo de Maxwell), essas "ondulações" foram produzidas e detectadas por Heinrich Hertz [3].

A identidade entre essas ondulações e a luz não era necessária para a conclusão da teoria eletromagnética de Maxwell. Muito pelo contrário, foi com essa hipótese, assumida após a conclusão de estudos relativos ao eletromagnetismo, que Maxwell desenvolveu outra teoria, a Teoria Eletromagnetica da Luz, exposta nos quatro últimos capítulos de seu tratado sobre eletromagnetismo. A partir dessa teoria foi que Maxwell passou em definitivo a optar pela aceitação da luz como "onda eletromagnética". Consequentemente, a "natureza problemática da vitória da teoria ondulatória", referida por Einstein e Infeld (vide capítulo VI - item VI.1), não implica necessariamente na inconsistência do modelo eletromagnético macroscópico de Maxwell.

III.2 - Teorias de emissão

Se raciocinarmos segundo Newton, os campos eletromagnéticos estacionários —campo elétrico e campo magnético— seriam, a exemplo do campo gravitacional, produzidos graças à emissão, pelos corpos materiais, de alguma coisa de natureza imaterial. [4] Classicamente falando, essa alguma coisa, sendo imaterial, não deveria transportar energia [5]. O termo energia foi utilizado, em sua plenitude física atual, posteriormente a Newton e somente a partir do século XIX começou a se pensar em energia contida nos campos estacionários. Não se deve confundir energia do campo com energia potencial, pois esta foi pensada inicialmente como uma energia contida em um objeto pelo fato dele se situar em um campo.

Por outro lado, se raciocinarmos segundo Maxwell, se a luz for absorvida por um corpo, este corpo torna-se aquecido, o que mostra que ele recebeu energia do exterior [6].

Se pretendermos compatibilizar os dois raciocínios (de Newton e de Maxwell), a única solução seria supormos que luz e onda eletromagnética seriam entidades emitidas pelos corpos, mas a representarem coisas distintas, ainda que possuam uma afinidade muito grande (a mesma fonte, os mesmos receptores, a mesma velocidade e um inter-relacionamento muito intenso entre ambas ao se encontrarem no espaço). Não obstante, Maxwell optou pela teoria mecânico-ondulatória tanto para os campos quanto para a luz e, portanto, pela suposição da não-emissão [6]; e a identidade propalada por Maxwell decorre desta opção. Ao que parece, em nenhum trecho de sua obra Maxwell chegou a assumir a possibilidade da existência de alguma coisa de natureza imaterial emitida pelos corpos materiais (o espírito da matéria de Newton - vide ítem I-2); ou seja, emissão para Maxwell seria emissão de matéria, não havendo nada de imaterial em sua teoria eletromagnética —nem mesmo o éter— a se assemelhar com o espírito da matéria newtoniano.

A teoria ondulatória clássica difere das teorias de emissão —seja material, seja imaterial— principalmente por assumir a existência de um meio etéreo a conter a energia que se propaga [6], seja cinética (vibrações do meio), seja potencial (elasticidade). Nada obsta a que se pense na existência de um éter imaterial, mas não foi essa a opção de Maxwell, pois ele deixa claro, em toda a sua obra, acreditar num comprometimento de natureza mecânica entre matéria e energia. Muitos na atualidade acreditam num éter imaterial ou, até mesmo, num éter a satisfazer os caprichos de uma matemática sofisticada. Einstein chega próximo a essa situação, deixando claro que essa idéia de éter poderia ser deixada de lado num estudo inicial [7].

III.3 - A representação das ondas eletromagnéticas

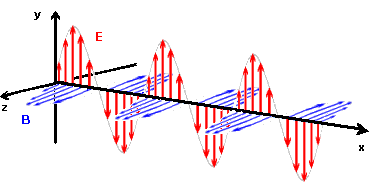
No estudo das ondas eletromagnéticas é costume dar uma ênfase toda especial às chamadas ondas planas, ou seja, aquelas que se propagam numa direção fixa. Com esta simplificação, a configuração mais simples seria aquela a representar um dos constituintes elementares da onda a percorrer um eixo retilíneo. Na figura 10 está representado um tipo padrão (onda senoidal) desses elementos propagando-se na direção x, com o campo elétrico E na direção y e o campo magnético B na direção z. Os campos E e B são sempre perpendiculares à direção de propagação e são perpendiculares entre si. Diz-se também que essa onda é linearmente polarizada [8], denominação esta a significar que o campo elétrico se restringe a ser paralelo a uma determinada reta do plano xy (no caso representado na figura, a reta considerada é paralela ao eixo y).

Figura 10: Onda eletromagnética plana, linearmente polarizada.

Uma figura semelhante, e com animação java, pode ser observada no site do Departamento de Física da UFSC [estando na internet, clique aqui para visualizar a imagem].

No estudo da óptica ondulatória é costume utilizar-se desta imagem (figura 10) para representar o componente mais simples da luz, aquele que virá, sob certos aspectos, a identificar-se com o fóton das teorias atuais, como veremos nos capítulos seguintes. Diz-se também que essa luz, linearmente polarizada, seria aquela emitida por um átomo individual, e o campo elétrico transversal da luz seria sempre dirigido num plano que contém a linha ao longo da qual oscila a distribuição de carga e a direção de propagação da luz [9].

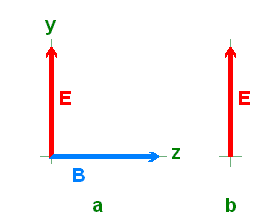
Costuma-se representar a onda eletromagnética da figura 10 através de sua imagem num plano perpendicular à direção de propagação (eixo x) e com o valor máximo para o vetor campo elétrico E, como mostrado na figura 11a. Pode-se ainda deixar de representar o vetor campo magnético B, como mostrado na figura 11b. Esta simplificação facilita o estudo de situações mais complexas, como veremos logo a seguir.

Figura 11: a) Onda eletromagnética plana observada na direção de propagação.
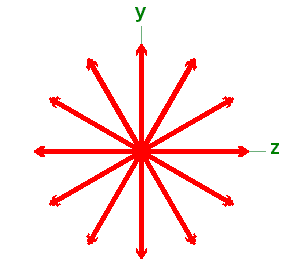
b) A mesma onda representada de maneira simplificada, apenas com o campo E.

Assume-se também que, via de regra, a onda eletromagnética emitida por uma coleção de átomos é não polarizada, porque não há relação entre a orientação da linha de oscilação das cargas num átomo e a orientação desta linha num outro átomo. Ocorrem então todas as polarizações possíveis e, portanto, não há polarização [9]. Representaremos essa onda não polarizada como mostrado na figura 12.

Figura 12: Representação esquemática da
onda eletromagnética não polarizada.

III.4 - Contraste onda-corpúsculo:

As figuras 10 e 11 devem ser comparadas, respectivamente, com as figuras 6 e 5 da representação corpuscular compatível com as idéias de Newton e apresentadas no capítulo I, item 3, sob o título os lados da luz). O campo E corresponde aos lados em cima e embaixo (giro polar) do raio de luz corpuscular, e o campo B corresponde aos lados direita e esquerda (giro equatorial). Nestas condições, a figura 13 ilustra o contraste que seria esperado observar entre as representações da teoria ondulatória eletromagnética atual e de uma possível teoria corpuscular da luz nos moldes newtonianos.

Figura 13: Luz ondulatória versus luz corpuscular.

Não é necessário que um raio de luz complexo apresente todos os componentes em todas as direções ao mesmo tempo. No caso eletromagnético ondulatório, isso significaria a anulação do campo E (soma vetorial). Em outras palavras, os raios elementares que entram na constituição de um raio de luz, via de regra não viajam concomitantemente, sendo mais provável que aconteça o que está representado na figura 14, a seguir, se bem que em visão de câmera excessivamente lenta. Como o comprimento de onda da luz visível é da ordem de 10^-6 metros e a velocidade da luz da ordem de 300.000 km/s, se fosse possível fotografar o pisca-pisca observado na figura 14 na frequência real, por melhor que fosse o flash utilizado, iríamos obter a figura 13 a sugerir uma estrutura cristalina, mesmo para um raio de luz dentre os considerados como de intensidade bastante baixa para o olho normal.

Figura 14: Representação dinâmica de um raio de luz não polarizada atravessando o plano da tela. Com essa imagem estamos pretendendo desfazer aquela estrutura aparentemente cristalina do esquema do raio de luz da figura 14, apelando-se para o artifício da câmera super lenta.

As figuras têm um valor didático que não deve ser hipervalorizado, qualquer que seja a teoria utilizada (corpuscular ou ondulatória). As flechas do campo elétrico não existem e a medida do campo refere-se a um valor localizado no ponto central do esquema. Assim também o raio de luz é uma entidade hipotética, a representar a trajetória dos corpúsculos que estão viajando segundo uma linha (vide figura 6 do capítulo I) e, portanto, deveriam ocupar também o ponto central do esquema. Consequentemente, a estrutura cristalina referida no parágrafo anterior é um artefato de representação, nada mais do que isso. O que não significa dizer que os corpúsculos de luz, na suposição de existirem, não poderiam simular imagens cristalinas no espaço, se bem que pertencentes a raios distintos.

---

 

Para ir para o próximo capítulo (Emissores e Receptores de luz)
clique na figura à direita Þ 

 

---